前言

作为一名文科生，学习编程最大的阻碍莫过于数学知识。

学习数学的必要性

跟开发APP和后台服务器相比，机器学习、深度学习需要大量的数学知识。

数据处理和清洗：数据分析涉及大量的数据处理和清洗工作，需要掌握基本的数学概念和方法。例如，对数据进行排序、过滤、聚合等操作时需要使用数学中的比较、筛选和统计等技巧。
统计分析：统计学是数据分析的基础，通过统计方法可以揭示数据背后的规律和趋势。学习数学中的概率论、假设检验、回归分析等知识，可以帮助我们进行数据的描述、推断和预测，有效地解释和利用数据。
建模和算法：在数据分析中，常常需要建立数学模型和运用算法进行数据挖掘和机器学习。数学中的线性代数、优化理论和机器学习算法等知识，为我们构建模型、选择合适的算法和优化参数提供了重要的基础。
数据可视化：数据分析的结果通常通过可视化手段展示，使得人们更容易理解和解释数据。数学中的图论和几何学等知识，能够帮助我们设计和创建有效的数据可视化图表和图形。
领域交叉：数据分析常常与其他学科领域相结合，如金融、市场营销、医疗等。学习数学能够为我们理解和应用特定领域的数据分析方法提供坚实的数学基础。

关于数学知识的学习，不建议大家啃教材，会浪费大家大量的精力和时间。只需掌握必要的关键性知识即可。

知识点概括

微积分知识点

导数与求导公式
- 导数表示函数在某一点的变化率，可以通过极限定义或常见函数的求导公式来计算。
- 常见的求导公式包括幂函数、指数函数、对数函数、三角函数以及其组合和反函数的求导规则。
导数与函数的单调性
- 导数可以帮助判断函数在某一区间的单调性。若导数在该区间上恒大于零，则函数在该区间上单调递增；若导数在该区间上恒小于零，则函数在该区间上单调递减。
函数极值判定法则
- 函数在极值点处的导数为零或不存在。利用导数的性质可以判断函数的极值点。
高阶导数
- 高阶导数表示函数的导数再次求导得到的结果。通过求高阶导数，可以研究函数的凹凸性、拐点等性质。
二阶导数与函数的凹凸性
- 函数的凹凸性可以通过二阶导数来判断。若函数在某一区间上的二阶导数恒大于零，则函数在该区间上是凹函数；若二阶导数恒小于零，则函数在该区间上是凸函数。
导数泰勒展开
- 导数泰勒展开是利用泰勒公式将函数表示为导数的级数展开形式。这个展开形式可以近似描述函数在某一点附近的行为，从而进行函数逼近和计算。

线性代数知识点

在机器学习的很多地方都用到了线性代数的知识，具体用到的知识点有：

向量
- 向量是具有大小和方向的量，可以进行加法、减法、数量乘法等运算。
矩阵和它的各种运算
- 矩阵是二维数组，具有行和列的结构。常见的矩阵运算包括加法、减法、乘法、转置和求逆等。
逆矩阵的定义与性质
- 逆矩阵是满足乘法运算下的单位元的矩阵。逆矩阵的性质包括可逆性、乘法交换律和分配律等。
二次型
- 二次型是关于向量的二次齐次多项式，可以用矩阵表示。二次型的研究与矩阵的特征值和特征向量相关。
矩阵的特征值与特征向量
- 矩阵的特征值与特征向量是描述矩阵性质的重要指标，它们与矩阵的对角化、对称性等密切相关。
矩阵的奇异值分解
- 矩阵的奇异值分解将矩阵分解为三个矩阵的乘积形式，可以用于数据降维、矩阵逆的计算等。

概率论知识点

随机事件与概率
- 随机事件与概率是概率论的基础概念，随机事件是指在一定条件下可能发生或不发生的事件，概率是描述随机事件发生可能性的数值
条件概率和贝叶斯公式
- 条件概率和贝叶斯公式描述了在已知某些条件下，发生另一事件的概率。
随机变量
- 随机变量是随机事件对应的数值，可以是离散型或连续型的。
随机变量的期望和方差
- 随机变量的期望和方差是描述其分布特征的重要指标。
常用概率分布
- 常用概率分布包括离散型分布（如二项分布、泊松分布）和连续型分布（如正态分布、指数分布）等。
协方差与协方差矩阵
- 协方差和协方差矩阵描述了随机变量之间的线性相关性和方差的关系。
最大似然估计
- 最大似然估计是一种用于估计参数的方法，基于已观测到的样本，寻找最有可能产生这些样本的参数值。它在统计建模和机器学习中具有重要应用。

最优化知识点

几乎所有机器学习算法归根到底都是在求解最优化问题。

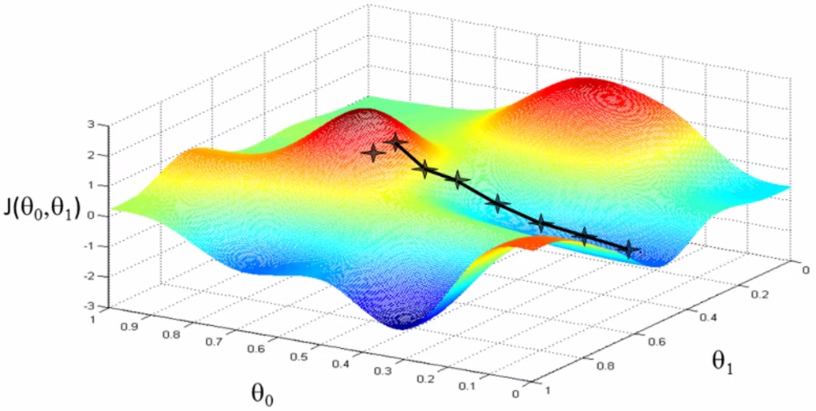
求解最优化问题的指导思想是在极值点处函数的导数/梯度必须为 0。因此你必须理解梯度下降法，牛顿法这两种常用的算法。凸优化是机器学习中经常会提及的一个概念，这是一类特殊的优化问题，它的优化变量的可行域是凸集，目标函数是凸函数。凸优化最好的性质是它的所有局部最优解就是全局最优解，因此求解时不会陷入局部最优解。如果一个问题被证明为是凸优化问题，基本上已经宣告此问题得到了解决。

在机器学习中，线性回归、岭回归、支持向量机、logistic 回归等很多算法求解的都是凸优化题。拉格朗日对偶为带等式和不等式约束条件的优化问题构造拉格朗日函数，将其变为原问题，这两个问题是等价的。通过这一步变换，将带约束条件的问题转换成不带约束条件的问题。

学习建议

建立坚实的数学基础：确保你对基本的数学概念和运算有清晰的理解，包括代数、三角函数、指数和对数等。如果你在这些基础知识上有缺漏，可以回顾相关的教材或参加在线课程进行学习。
学习逐步进行：将数学知识点分解为小的、可管理的部分，逐步学习和掌握。从基本的概念和定义开始，逐渐深入学习推导和应用。
练习和解决问题：数学是一门需要实践的学科，通过大量的练习和解决问题来加深理解。找到相关的练习题和习题集，积极参与课堂练习和在线社区的讨论。
利用在线资源：有许多免费和优质的在线资源可供学习数学知识，如网上教程、视频课程和在线学习平台。选择适合自己学习风格的资源，进行系统学习和实践。
寻找实际应用场景：将数学知识与实际应用场景结合起来，可以更好地理解和应用。在数据分析和机器学习领域，寻找相关的案例和项目，将学到的数学知识应用到实际问题中。
与他人讨论和合作：与他人讨论数学问题和解决方法，可以加深理解和促进思维的交流。参加学习小组、线上论坛或社区，与其他学习者分享和互动。
持续学习和实践：数学是一个连续的学习过程，需要不断地巩固和扩展知识。保持学习的动力和耐心，坚持实践和应用数学知识，不断提升自己的能力。