2021年国赛高教杯数学建模
D题 连铸切割的在线优化
原题再现
连铸是将钢水变成钢坯的生产过程,具体流程如下(图 1):
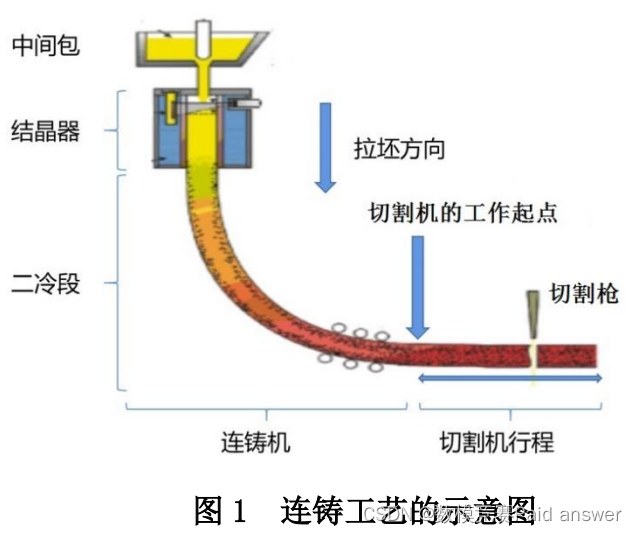
钢水连续地从中间包浇入结晶器,并按一定的速度从结晶器向下拉出,进入二冷段。钢水经过结晶器时,与结晶器表面接触的地方形成固态的坯壳。在二冷段,坯壳逐渐增厚并最终凝固形成钢坯。然后,按照一定的尺寸要求对钢坯进行切割。
在连铸停浇时,会产生尾坯,尾坯的长度与中间包中剩余的钢水量及其他因素有关。因此,尾坯的切割也是连铸切割的组成部分。
切割机在切割钢坯时,有一个固定的工作起点,钢坯的切割必须从工作起点开始。在切割过程中,切割机骑在钢坯上与钢坯同步移动,保证切割线与拉坯的方向垂直。在切割结束后,再返回到工作起点,等待下一次切割。
在切割方案中,优先考虑切割损失,要求切割损失尽量小,这里将切割损失定义为报废钢坯的长度;其次考虑用户要求,在相同的切割损失下,切割出的钢坯尽量满足用户的目标值。
在浇钢过程中,结晶器会出现异常。这时,位于结晶器内部的一段钢坯需要报废,称此段钢坯为报废段(图 2)。当结晶器出现异常时,切割工序会马上知道,以便立即调整切割方案。
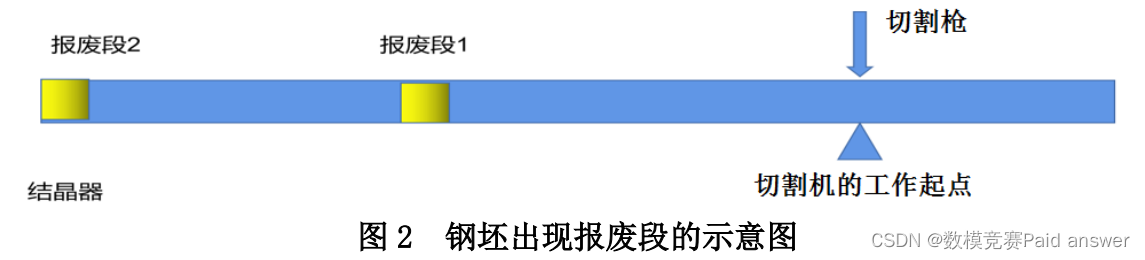
切割后的钢坯在进入下道工序时不能含有报废段。当钢坯出现报废段时,先通过切割机切断附着有报废段的钢坯,然后通过离线的二次切割,使余下的钢坯符合下道工序要求的长度;其他进入下道工序的钢坯也必须满足下道工序的长度要求。
现请你们团队建立数学模型或设计算法,解决以下问题:
问题 1 在满足基本要求和正常要求的条件下,依据尾坯长度制定出最优的切割方案。假定用户目标值为 9.5 米,目标范围为 9.0~10.0 米,对以下尾坯长度:109.0、93.4、80.9、72.0、62.7、52.5、44.9、42.7、31.6、22.7、14.5和 13.7(单位:米),按“尾坯长度、切割方案、切割损失”等内容列表给出具体的最优切割方案。
问题 2 在结晶器出现异常时,给出实时的最优切割方案:(1)在钢坯第 1次出现报废段时,给出此段钢坯的切割方案;(2)在出现新的报废段后(如图 2),给出新一段钢坯的切割方案和当前段钢坯切割的调整方案,或声明不作调整。
假设结晶器出现异常的时刻在 0.0、45.6、98.6、131.5、190.8、233.3、266.0、270.7 和 327.9(单位:分钟),用户目标值是 9.5 米,目标范围是 9.0~10.0米。在满足基本要求和正常要求的条件下,按“初始切割方案、调整后的切割方案、切割损失”等内容列表给出这些时刻具体的最优切割方案。
问题 3 假设实时最优切割方案和结晶器出现异常的时刻均与问题 2 相同,在满足基本要求和正常要求的条件下,对(1)用户目标值是 8.5 米,目标范围是 8.0~9.0 米,(2)用户目标值是 11.1 米,目标范围是 10.6~11.6 米两种情况分别按“初始切割方案、调整后的切割方案、切割损失”等内容给出具体的最优切割方案。
附录:参数与要求
工艺参数:切割机切断一块钢坯的时间为 3 分钟,切割后,返回到工作起点的时间为 1 分钟。从结晶器中心到切割机工作起点处钢坯的长度是 60.0 米,连铸拉坯的速度为 1.0 米/分钟。当结晶器出现异常时,报废段的长度是 0.8 米。
基本要求:切割后的钢坯长度必须在 4.8~12.6 米之间,否则无法运走,阻碍生产。下道工序能够接受的钢坯长度是 8.0~11.6 米,如果不在此范围内,可以将钢坯运走进行二次离线切割,但切割下的部分报废,从而产生损失。例如,12.6 米的钢坯切掉 1.0 米变成 11.6 米,切下来的 1.0 米报废;而小于 8.0 米的钢坯只能全部报废。
正常要求:正常切割是按照用户要求的长度进行切割。用户要求包含目标值和目标范围,钢坯的切割长度应尽量满足目标值,而在目标范围内的长度也是可以接受的。例如,目标值是 9.5 米,目标范围是 9.0~10.0 米,则切割长度尽量是 9.5 米,而在 9.0~10.0 米之间的长度是允许的。当钢坯长度不在目标范围内时,会产生损失。例如,钢坯长度是 11.6 米,多出来的 1.6 米报废。
整体求解过程概述(摘要)
本文主要针对连铸切割的问题,基于附录给出的参数、钢坯长度的要求以及用户的不同目标值,建立数学模型以制定具体的最优切割方案。
针对问题一,首先以尾坏的切割损失最小、切割长度为9.5米的根数最多以及切害长度为9.0-10.0米的根数最多建立多目标规划模型。然后,通过序贯解法,以切割损失最小为目标函数、以尾坯长度为约束求解最优,将得到的最优解看做约束条件放入第一个目标(即切割长度为9.5米的根数最多)求解最优。接着,将前两个目标的最优解看做约束条件一并放入第三个目标求解最优,得到多目标规划模型的最优解。最后,将12个尾坯长度分别带入模型,利用matlab解得不同尾坯的最优切割方案和切割损失。
针对问题二。对于第一小问,首先以钢坏的切制损失最小,切割长度为9.5米的机数最多以及切割长度为90-100米的根数最多三个目标建立多目标规划模型。然后,对除去0.8米的报废段剩下的44.8米的钢坯进行分析,利用matlab给出具体切割方案,见表2,在此基础上,将0.8米报废段附着于4.8米的最小损失段一起切除,给出具体切割方案,见表3。最后,将报废段之前还存在60.0米或64.0米长度的钢坯与所需的切割长度(45.6米)结合,得出最终的最优切割方案。对于第二小问,首先利用问题二的模型,得到在出现新的报废段后,新一段钢坏的切割方案,见表5。基于此方案与相关的工艺参数,进一步得到实时的最优切割方案。见表 6。然后,为了得到当前毁钢坏切制的事优调整方案,采用两种方法求能初始切害方案。方法一:假定第n个时间窗口(n≥3),仅第n-1个时间窗口无异常,其他时间窗口均有异常。得到从第3-9个窗口中每个窗口均往前2个异常时刻,除去0.8米报废段后的具体切割方案,再将7个时间段的切割方案分别加上该时间段之前每个时间单元的切割方案,得到初始切割方案,见表7。方法二:假定所有时间窗口均无异常。分别求出后7个窗口之前所有时间单元的切割方案之和即得到初始切割方案,见表 9。最后,通过对比分析发现方法一所得出的切割方案更贴近调整后的切割方案。据此,将方法一得到的初始切割方案与调整后的切割方案以及切割损失情况进行整合得到所有时刻具体的最优切割方案。
针对问题三,首先相据用户要求,以钢坏的切制福失量小、切割长度为8.5米的根数最多以及切割长度为8.0-9.0米的根数最多三个目标建立多目标规划模型。然后利用问题二得出的更优方法(即方法一),得到初始切割方案与调整后的切判方案以及最终切割方案并计算出切割损失,见表14。同理得用户目标值是11.1米、目标范围是10.6-11.6米的最优切割方案。
模型假设:
1.结晶器出现异常时,立即出现报废段。
2.结晶器在0.0时刻出现异常时,切割机在工作起点处等待切割。
3.钢坯长度只保留一位小数。
问题分析:
问题一的分析
要在满足基本要求和正常要求的条件下依据尾坯长度制定出最优的切割方案,由于在切割方案中需要优先考虑切割损失,并要求切割损失(报房钢坯的长度)尽量小,其次考虑用户要求,在相同的切割损失下应尽量满足用户的目标值,因此可以建立多目标规划模型,通过序贯解法,将目标按其重要程度不同优先等级,依次转化为多个线性规划模刑,以109.0米的屋坏长府为例,先以切割损失最小作为目标得出初步切割方案。再以钢坯长度为9.5米的根数最多作为目标得出进一步的切割方案,最后以钢坯长度范围在9.0-10.0米的根数最多为目标得出最终切割方案。
问题二的分析
首先要得到钢坏第一次出现报废段时,此段钢坯的切割方案,可以考虑到当结晶器出现异常时,结晶器内部的一段钢坏会立即报废,且切割后的钢坏在进入下道工序时不能含有报废段,如钢坯出现报废段,则可以通过离线的二次切割,使余下的钢坯符合下道工序要求的长度,因此我们可以考虑将0.8米的报废段附着在其他钢坯上,针对剩下的44.8米的钢坏,可以建立多元目标规划模型得出具体切割方案,如果具体切割方案中存在切割损失时,报废段附着在最小损失段一起切除,当不存在切割损失时,将其附着在最长段一起切割,然后再通过离线的二次切割将其与满足要求的钢坏分离。另外,当结晶器出现异常时,报废段是在结晶器中产生的,在这段报废段之前二冷段中已经产生钢坏。因为从结晶器中心到切割机工作起点处钢坏的长度是60.0米,而切割机切断一块钢坯的时间为3分钟,切割后返回到工作起点的时间为1分钟,切割机与连铸拉还同步运动的速度为1.0米/分钟。当出现报废段时无法判断切制机所处位置,在此可以只考虑切割机在起点等待切割和刚好开始切钢坯这两种情况,所以在报废段之前还存在 60.0米或64.0米长度的钢坯,然后通过模型求出60.0米和64.0米钢还的具体切方案,再将60.0米和64.0米钢还的具体切方案加上44.8米的具体切方案,即得到钢坏第一次出现报废段时,此段钢坯的切割方案。
其次,要得到出现新的报废段后,新一段钢坯的切割方案,同理于求解钢坯第一次出现报废段时,此段钢坯的切割方案所建立的模型,考虑将0.8米的报废段附着在其他钢坏上,针对剩下的钢坏,给出具体切割方案。
接着,要求出现报废段后当前段钢坯的调整方案,方案的调整可理解为是由于这9个时刻点中某些时刻从无异常到有异常所导致的,可以采用两种方法进行求解,首先定义以每个异常时刻为时间窗口,则有9个窗口,以相邻两个异常时刻为时间单元,则有8个时间单元,对于初始切割方案的理解,方法一认为是在仅当前段钢坯的倒数第二个时间窗口无异常,且此前所有时间窗口为有异常的条件下,从第3个窗口至第9个窗口每个窗口均往前2个异常时刻计算除去0.8米报废段后的钢坏长度,得到7个钢坏长度,再根据问题二中求解钢坏第1次出现报废段时钢坏的切割方案所建立的模型求出其最优切割方案。然后,将7个时间段的切割方案分别加上该时间段之前每个时间单元的切割方案,而方法二认为在所有时间窗口均无异常的条件下,第 3 个窗口至第9个窗口共7个窗口,分别求出这7个窗口的之前所有时间单元的切割方案之和。而对于调整后的切割方案的理解,两种方法都认为是在所有时间窗口均无异常的条件下,第3 个窗口至第9个窗口,共7个窗口,分别求出这7个窗口的之前所有时间单元的切割方案之和。然后根据建立的模型分别求出方法一方法二的初始切割方案和调整后的切割方案最后通过对比得出当前段钢坯的调整方案。
最后,要给出结晶器出现异常时的实时最优切割方案,由于结晶器从0.0时刻出现异常时无法判断切割机所处位置,在此只考虑切割机在起点等待切割的情况,此时从结晶器中心到切割机工作起点处钢坯的长度是60.0米,又已知连铸拉坯的速度为1.0米分钟,所以0.0时刻出现的报废段需要经过60.0分钟才能来到工作起点,因此可以先对结晶器中心到切割机工作起点处长度为 60.0 米的钢还进行切割,然后根据后面每个时间单元的最优切割方案来制定实时的最优切割方案。
问题三的分析
要在实时最优切割方案和结晶器出现异常的时刻均与问题二相同,且满足基本要求和正常要求的条件下,按“初始切割方案、调整后的切割方案、切割损失”分别给出对目标值为8.5米11.1 米,目标范围为8.0-9.0米和10.6-11.6米的具体最优切方案,此题同理于问题二求解用户目标值是9.5米,目标范围是9.0-10米的具体最优切方案所建立的模型。首先根据用户要求,以钢坏的切割损失最小、切割长度为8.5米的根数最多以及切割长度为8.0-9.0米的根数最多三个目标建立多目标规划模型。然后利用问题二得出的更优方法,根据所建立的模型解得初始切割方案与调整后的切割方案并计算出切割损失,同理得用户目标值是11.1米、目标范围是10.6-11.6米的最优切割方案。
模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
k=[44.8 52.2 32.1 58.5 41.7 31.9 56.4];
k=k(1);%现在求的是 0.0-45.6 这个时间段中除去开头 0.8 米报废段的钢还的最优切割方案,如果要求其它时间段钢坯长度的最优切割方案只需要更改k 中括号内的数字
f1=zeros(1,79)
f1(1,1:32)=[4.8:0.1:7.9]
f1(1,44:79)=[9.1:0.1:12.6]
intcon=[1:79];
a=[];
b=[];
aeq1=[4.8:0.1:12.6];
beq1=k;
lb=zeros(79,1);
ub=[];
[x1,y1]=intlinprog(f1,intcon,a,b,aeq1,beq1,lb,ub);
x1=x1',y1;
f2=zeros(1,79);
f2(1,38)=-1;
c2=zeros(1,79);
c2(1,1:32)=[4.8:0.1:7.9];
c2(1,44:79)=[9.1:0.1:12.6];
aeq2=[4.8:0.1:12.6;c2];
beq2=[k,y1];
[x2,y2]=intlinprog(f2,intcon,a,b,aeq2,beq2,lb,ub);
x2=x2';
y2=-y2
f3=zeros(1,79);
f3(1,33:43)=-1;
c3=zeros(1,79);
c3(1,1:32)=[4.8:0.1:7.9];
c3(1,44:79)=[9.1:0.1:12.6];
d(1,38)=1;
aeq3=[4.8:0.1:12.6;c3;d]
beq3=[k,y1,y2];
[x,y]=intlinprog(f3,intcon,a,b,aeq3,beq3,lb,ub);
x=x';
y=-y