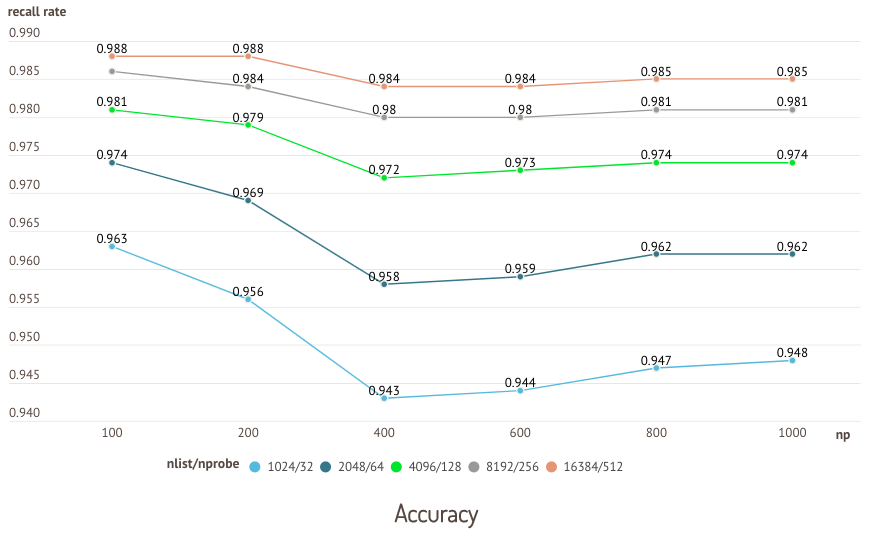
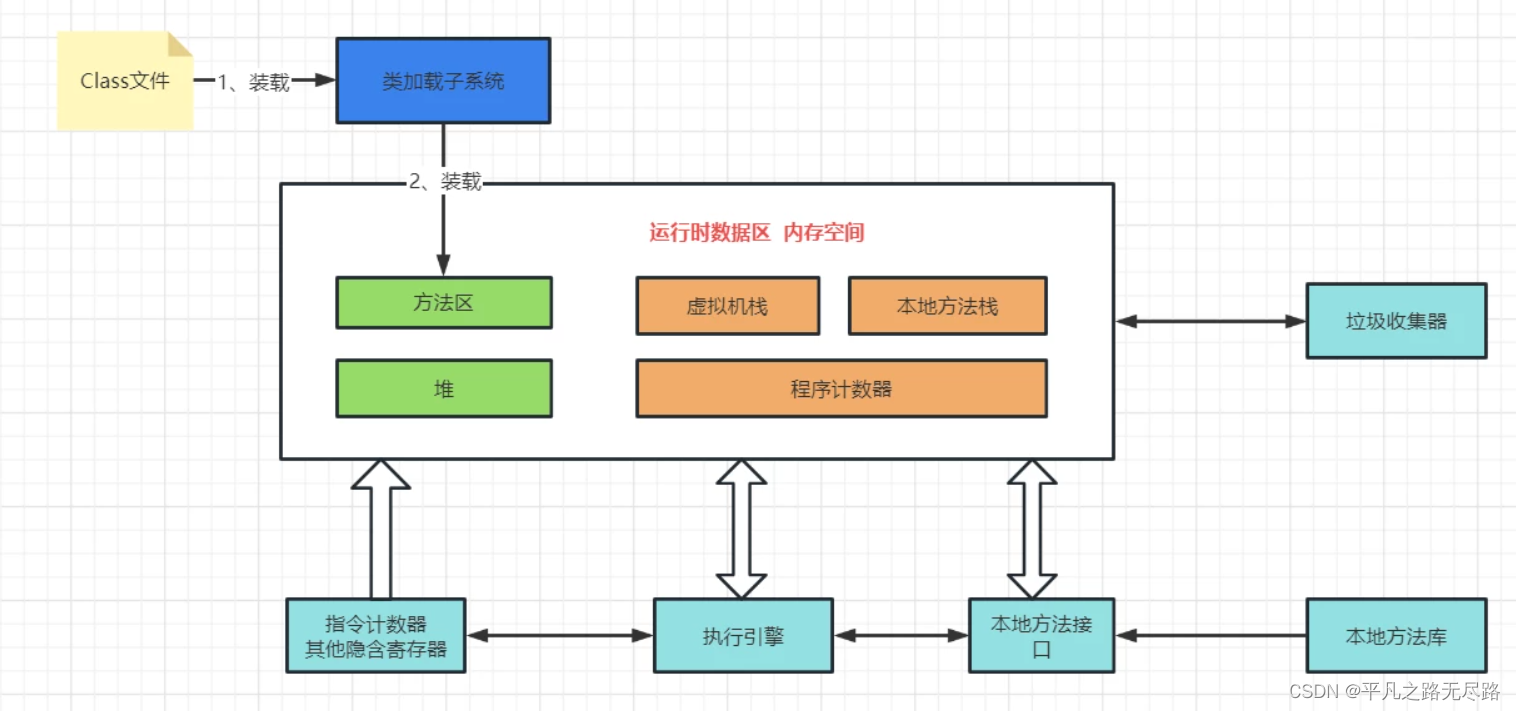
数据结构–算法时间复杂度
在计算算法时间复杂度的时候,我们可以忽略表达式某些部分。
eg:
T
1
(
n
)
=
3
n
+
3
T_1(n) = 3n + 3
T1(n)=3n+3 ⇒
O
(
n
)
O(n)
O(n)
T
2
(
n
)
=
n
2
+
3
n
+
1314
T_2(n) = n^2+3n+1314
T2(n)=n2+3n+1314 ⇒
O
(
n
2
)
O(n^2)
O(n2)
T
3
(
n
)
=
n
3
+
2
n
2
+
1314520
T_3(n) = n^3 + 2n^2+1314520
T3(n)=n3+2n2+1314520 ⇒
O
(
n
3
)
O(n^3)
O(n3)
加法规则
T
(
n
)
=
T
1
(
n
)
+
T
2
(
n
)
=
O
(
f
(
n
)
)
+
O
(
g
(
n
)
)
=
O
(
m
a
x
(
f
(
n
)
,
g
(
n
)
)
)
T(n)= T_1(n)+ T_2(n) = O(f(n))+ O(g(n)) = O(max(f(n), g(n)))
T(n)=T1(n)+T2(n)=O(f(n))+O(g(n))=O(max(f(n),g(n)))
多项相加,只保留最高阶的项,且系数变为1
乘法规则
T
(
n
)
=
T
1
(
n
)
×
T
2
(
n
)
=
O
(
f
(
n
)
)
×
O
(
g
(
n
)
)
=
o
(
f
(
n
)
×
g
(
n
)
)
T(n)= T_1(n)×T_2(n)= O(f(n))×O(g(n)) = o(f(n)×g(n))
T(n)=T1(n)×T2(n)=O(f(n))×O(g(n))=o(f(n)×g(n))
多项相乘,都保留
eg:
T
(
n
)
=
n
3
+
n
l
o
g
2
n
=
O
(
n
3
)
+
O
(
n
2
l
o
g
2
n
)
=
O
(
n
3
)
T(n)= n^3 +nlog_2n= O(n^3)+ O(n^2log_2n) = O(n^3)
T(n)=n3+nlog2n=O(n3)+O(n2log2n)=O(n3)
公式
O ( 1 ) < O ( l o g 2 n ) < O ( n ) < O ( n l o g 2 n ) < O ( n 2 ) < O ( n 3 ) < O ( 2 n ) < O ( n ! ) < O ( n n ) \color{red}O(1)<O(log_2n)< O(n)< O(nlog_2n)< O(n^2)<O(n^3)<O(2^n)< O(n!)< O(n^n) O(1)<O(log2n)<O(n)<O(nlog2n)<O(n2)<O(n3)<O(2n)<O(n!)<O(nn)
结论
结论 1 : 顺序执行的代码只会影响常数项,可以忽略 \color{red}结论1:顺序执行的代码只会影响常数项,可以忽略 结论1:顺序执行的代码只会影响常数项,可以忽略
结论 2 : 只需挑循环中的一个基本操作分析它的执行次数与 n 的关系即可 \color{red}结论2:只需挑循环中的一个基本操作分析它的执行次数与n的关系即可 结论2:只需挑循环中的一个基本操作分析它的执行次数与n的关系即可
几种时间复杂度
-
最坏时间复杂度 \color{red}最坏时间复杂度 最坏时间复杂度:最坏情况下算法的时间复杂度。
-
平均时间复杂度 \color{red}平均时间复杂度 平均时间复杂度:所有输入示例等概率出现的情况下,算法的期望运行时间。
-
最好时间复杂度:最好情况下算法的时间复杂度
知识点回顾 & 重要考点