量子位 | 公众号 QbitAI

鹅妹子嘤，天才数学家陶哲轩搞数学研究，已经离不开普通人手里的“数学菜鸡”GPT了！

就在他最新解决的一个数学难题下面，陶哲轩明确指出自己“使用了GPT-4”，后者给他提出了一种可行的解决方法。

借助GPT-4，他不仅成功地突破了这一难题，还将答案分享在了MathOverflow上：

它给我提供了最终的解题思路，接下来我只需要继续计算就行。

为了给更多数学家分享用GPT-4工作的便利性，陶哲轩还将自己的聊天记录po了出来，里面完整地记载了他和GPT-4的对话。

可以看见，在这份聊天记录中，他把GPT-4称呼为“专业数学合作者”，而不仅仅是一个普通的数学助手。

这个身份属实不一般了，不知道之后陶哲轩写论文的时候会不会把GPT-4列为共同作者（手动狗头）。

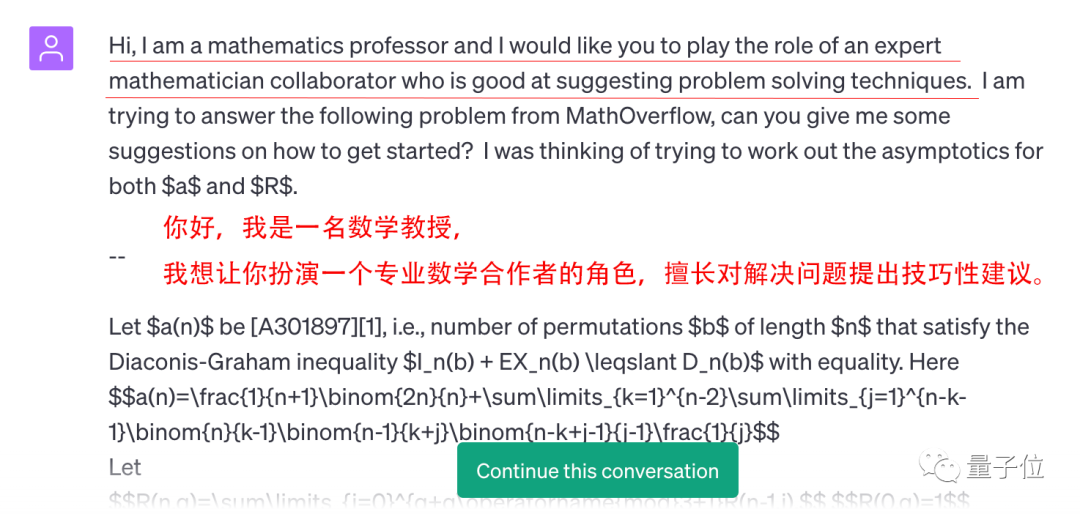
不仅如此，戳对话记录底部的“continue this conversation”按钮，还能一键把对话记录导入自己的ChatGPT中，突然闯入人类大师和AI的交谈。

陶哲轩解决了什么新问题？

陶哲轩研究的问题，是一个两天前在数学网站MathOverflow上更新的提问。

这个名叫“优雅的递归之A301897”问题，具体长这样：

其中，A301897是一个被整数数列网站OEIS收录的数列：

这个数列中有一系列来自长度为n的排列b的数，它们有一个共同点，就是满足Diaconis-Graham不等式且等号成立。

Diaconis-Graham不等式由戴康尼斯（Persi Diaconis）和葛立恒（没错，就是“最大数”之父Ronald Graham）于1977年共同提出，属于概率统计方面的研究。

显然，这一大段提问中不仅夹杂着大量专业数学公式，而且还涉及需要跳转的网页资料。

作为数学公认不太好的“数学菜鸡”，GPT-4真的能像一名专业数学家那样快速读懂公式、给出解决问题的专业建议吗？

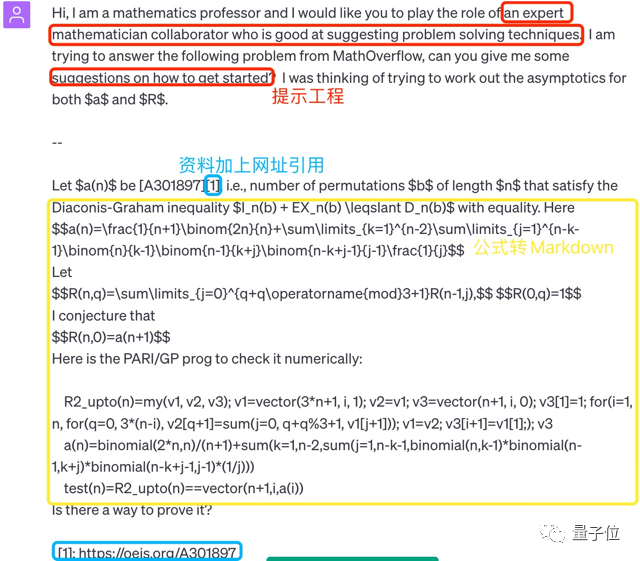
事实上，相比直接把问题复制粘贴给GPT-4，陶哲轩做了三件事：

• 首先，做一些提示工程，明确GPT-4的“身份”和“目标”。其中身份是“一个擅长给技巧性建议的数学合作专家”，目标是“提供一些建议”而非解决问题。

• 然后，相比直接把大段公式复制进GPT-4提问栏（确实可以这样做），陶哲轩选择将问题描述转成Markdown格式。

• 最后，涉及需要GPT-4自己查找资料的内容，陶哲轩将它转变成一个引用注释，并在结尾给出网址。

完整的提问过程长这样：

也就是说，相比让GPT-4直接化身数学家去“解决问题”，陶哲轩只是把它当成一个提供灵感来源的“专家”，给自己建议一些研究的方向。

GPT-4很快给出了8个具体的建议：

1、理解问题：在深入证明之前，确保你理解了问题中的每一项。如果你不熟悉Diaconis-Graham不等式，研究一下它，了解表达式a(n)和R(n, q)中的每一项代表什么。

2、简化表达：有时候，复杂的表达可以被简化。例如，你可能想看看表达式中a(n)的二项式系数是否可以简化，或者是否可以用更简单的方式计算总和。

3、归纳法：由于R(n, q)是递归定义的，因此证明猜想的一种自然方法是使用数学归纳法。你可能想要证明，如果这个猜想对n成立，那么它对n+1也成立。

4、生成函数：另一种方法是使用生成函数。尝试找到a(n)和R(n, 0)的生成函数，然后证明它们是相等的。这有时可以把一个复杂的组合问题变成一个更简单的代数问题。

5、渐近分析：正如你提到的，分析a(n)和R(n, 0)的渐近行为可能会对它们的关系有一些深入的了解。这有时可以用斯特林的阶乘近似来实现，或者通过分析表达式中的主导项来实现。

6、数值证据：虽然不是证明，但收集数值证据有时可以让我们了解如何证明一个猜想。因为你有PARI/GP代码，可以用数值来检查猜想，你可能想读一读每个序列的前几项，看看是否能发现任何模式。

7、寻找类似问题：有时，一个问题或猜想是一个已知问题的泛化或变体。在组合文献中寻找类似的问题或定理，看看它们的证明是否可以适用于这个问题。

8、寻求反馈和合作：不要犹豫，从同事那里寻求反馈，或者在MathOverflow这样的论坛上发布你的部分结果。协作和同行评议通常是解决复杂数学问题的关键。

最终，陶哲轩使用建议4，也就是生成函数的方法，成功解决了问题。

当然，解决问题的过程并不需要用到GPT-4，采用MAPLE工作表+纸笔手动计算就能完成。陶哲轩也尝试了渐进分析（建议5）的方法，不过事实证明还是用生成函数更有效。

简单来说，陶哲轩只是用GPT-4给自己提供不同的解题思路，也就是“解题灵感”，但具体怎么解答，也就是更加数学的方法，他则不会交给GPT-4来完成。

至于“查资料”这种GPT-4的应用，陶哲轩也发挥到了极致。

例如在思考问题时，他还会把自己的“灵光乍现”拿出来和GPT-4讨论一下，例如他觉得这个问题和卡特兰数（Catalan numbers）有相似之处，希望GPT-4帮他查找一下对应的资料。

GPT-4很快给出了对应的回答，这也促使陶哲轩对另一个问题产生了新的灵感。

简单来说，陶哲轩在短短两段与GPT-4的对话中，展示了数学家使用GPT-4的正确姿势——找灵感和查资料。

这样一来，即使“数学菜鸡”如GPT-4，也能成为数学家的AI助理了。

大佬是怎么玩儿GPT的

分享人类大师和AI的聊天记录之余，陶哲轩的乳齿象博文里还附带着一份贴心指南，是他使用ChatGPT和GPT-4的经验之谈。

根据他过去的实操经验，最要紧的第一点：

不要试图让AI直接回答问题，因为这几乎肯定会得到一些看起来专业的废话。

为了避免GPT成为废话文学大王，行之有效的方案如下：

让AI扮演合作者的角色，而后让它提供策略建议。

Like this：

除此之外，“数学菜鸡”GPT，在大数学家手里能有什么用处？

陶哲轩大概的意思是酱婶儿的：

ChatGPT数学能力虽然不咋滴，但对做学术研究的人来说是个发散思维的好工具。

（对普通人来说有点不太专业，但对搞数学的学术人员来说刚刚好）

怎么解释用来“发散思维”这句话呢？

陶哲轩表达出来的观点是，既然ChatGPT在具体数学问题上给出的答案是不完全正确的，那不如索性发挥发挥它生成答案部分正确的特性。

简而言之，就是让它帮你找灵感balabalabla：

在处理数学问题时，可以让ChatGPT这类大语言模型做一些半成品的语义搜索工作。
也就是说，ChatGPT不用提供确切的答案，只用生成一些可能的提示。

这样一来，依据GPT生成的提示+传统搜索引擎搜索，就能很轻松get答案。

而且他还自曝，在GPT-4发布之前，他本人就从微软那里获得了访问资格。

也就是和微软154页《AGI的火花》论文里同款，未经过安全训练但能力更强的满血版。

从陶哲轩的反馈中可以看到，GPT-4非常擅长在和人类对话时进行一些cosplay，比如充当富有同情心的倾听者、热情洋溢的反馈者、富有创造力的灵感来源、翻译者或教师，或者是魔鬼的代言人。

与此同时，对于AI在数学研究中的表现，陶哲轩给出的大胆却又严谨的预言：

当与形式证明验证器、互联网搜索和数学符号包等工具整合时，2026年的AI，如果使用得当，将成为数学研究中值得信赖的共同作者，而且在许多其他领域也是如此。

除了数学研究，GPT-4已经是陶哲轩生活中的全方位小助手了。

他经常使用GPT-4回答一些随意、措辞含糊的问题，这些问题以前需要在搜索引擎里精心调整关键词才行。

还有位同事，因为亲戚拿到重症诊断而郁郁寡欢。为此，陶哲轩让大手一挥，让GPT-4洋洋洒洒写了封慰问信。

结果呢？同事眼含热泪，被感动哭了。

最后说回陶哲轩用GPT-4解决数学难题这事儿上来。

在MathOverflow下，有的网友觉得他不应该用GPT来回答数学问题，感觉是个很敏感的话题。

但还是有人表示了资瓷，表示觉得真的是泰库辣～

陶哲轩倒是毫不避讳地站出来表明了自己的立场，他倒不觉得有啥不好：

现在的担忧，跟维基百科流行初期时大家讨论的重点也没啥区别……
现在在维基百科上get初始线索，并且在引为论点时附上链接，展现它是我论据的一部分，都是大伙儿习以为常的事情。

并且陶哲轩看法还挺坚定，那就是“相信大家以后也会觉得用GPT来支持研究，没啥不妥当的呢”～

加入陶哲轩和GPT-4的对话：
https://chat.openai.com/share/53aab67e-6974-413c-9e60-6366e41d8414