树的基本概念

树是数据结构中的一个重要组成部分，它具有一对多的特点，是相对复杂的一种数据结构。书中是这样定义树的：
树是n个节点的有限集。在任意一颗非空树中：

有且仅有一个特定的称为根的节点；
当n>1时，其余节点可分为m个互不相交的有限集T1，T2，……，Tm，其中每一个集合本身又是一棵树，并且称为根的子树。
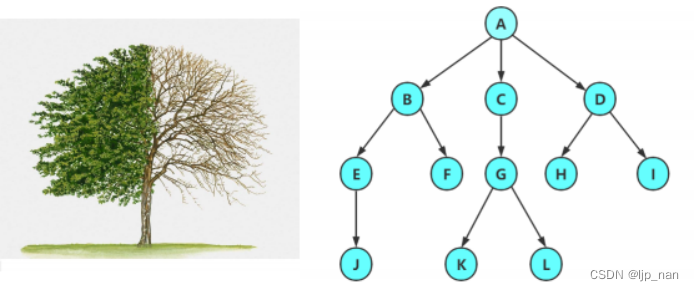
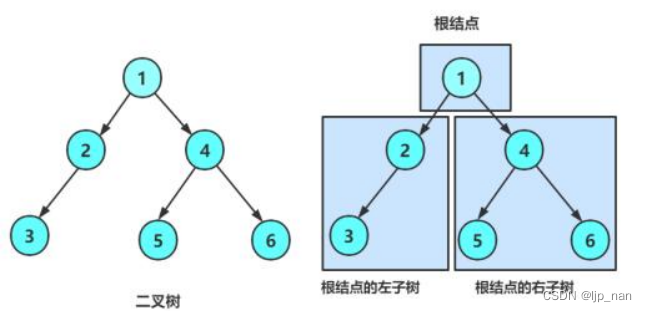
如下图所示：

A为根，B,C,D都是A 的子树。树是递归定义的，每一个根的下面都有子树。
树的表示可以是这样的：
1.树型表示法
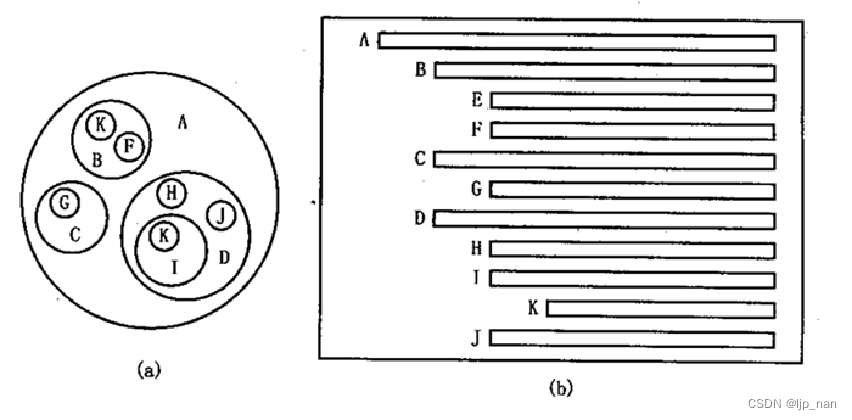
2.嵌套集合表示法: 如图(a)
3.凹入表示法: 如图(b)
4.广义表表示法: (A(B(EF), C(G), D(HI(K)J)))

树的基本术语

节点的度 ：一个节点含有的子树的个数称为该节点的度；如下图： A的为6
叶节点或终端节点：度为0的节点称为叶节点；如下图： B、C、 H、 I…等节点为叶节点
非终端节点或分支节点：度不为0的节点；如下图： D、 E、 F、G…等节点为分支节点
双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；如下图： A是B的父节点
孩子节点或子节点 ：一个节点含有的子树的根节点称为该节点的子节点；如下图： B是A的孩子节点
兄弟节点：具有相同父节点的节点互称为兄弟节点；如下图： B、C是兄弟节点
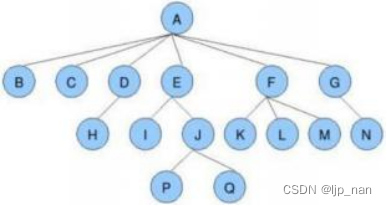
树的度 ：一棵树中，最大的节点的度称为树的度；如下图：树的度为6
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
树的高度或深度：树中节点的最大层次；如下图：树的高度为4
堂兄弟节点：双亲在同一层的节点互为堂兄弟；如下图： H、 I互为兄弟节点
节点的祖先：从根到该节点所经分支上的所有节点；如下图： A是所有节点的祖先
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如下图：所有节点都是A的子孙
森林：由 m（ m>0）棵互不相交的树的集合称为森林；

树的表示

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，既然保存值域，也要保存结点和结点之间的关系，实际中树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法
等。我们这里就简单的了解其中最常用的孩子兄弟表示法。

双亲表示法:

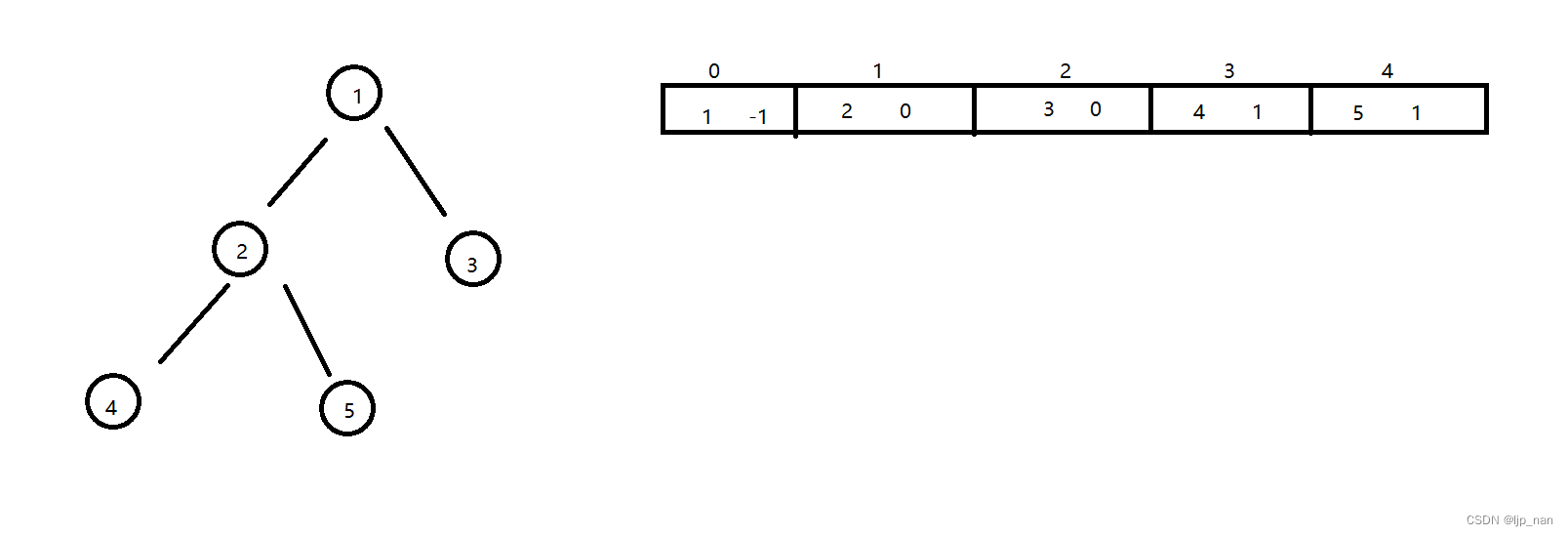
指的是一个结构体里有数据和双亲的下标。如下图所示
我们表示一个树：

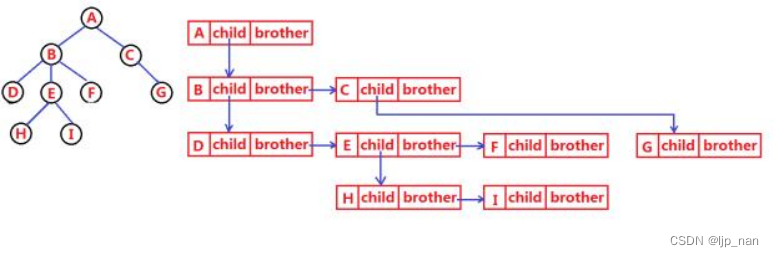
孩子兄弟表示法:

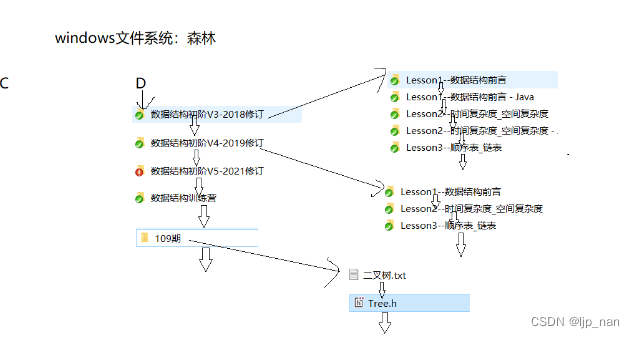
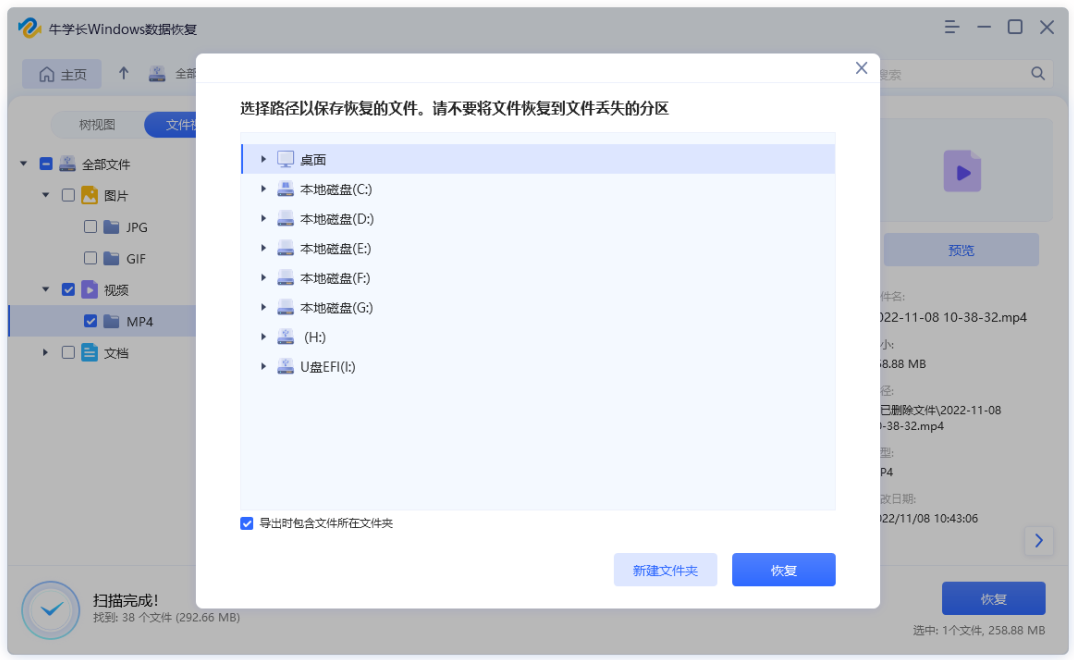
树的典型应用——目录树

windows的目录树
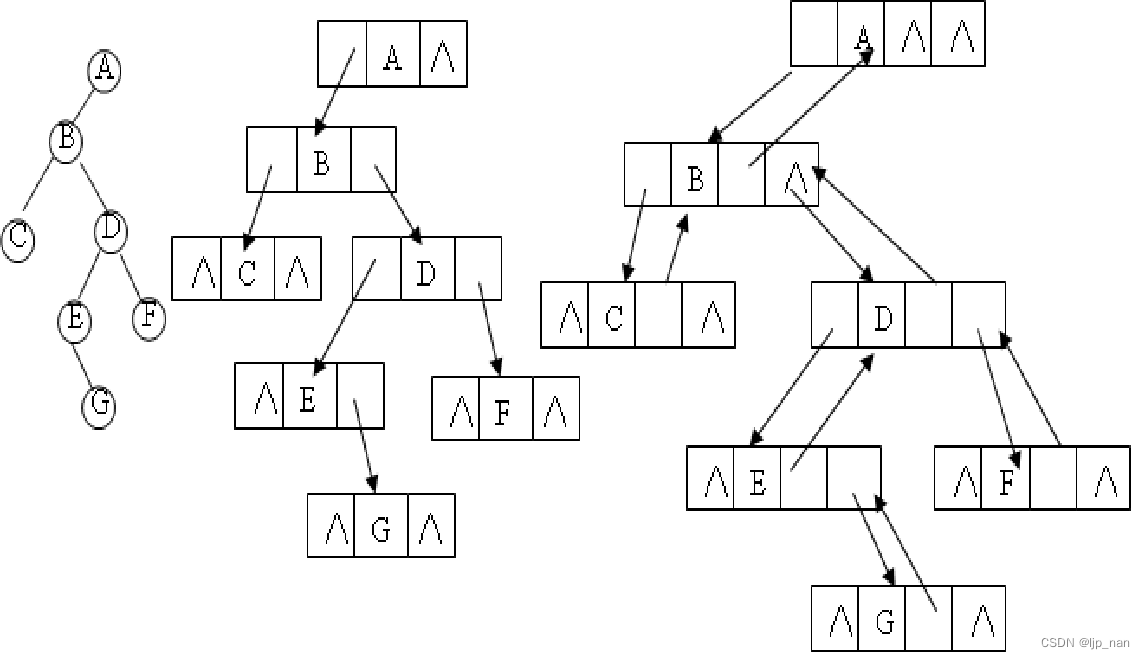
使用孩子兄弟表示法表示的树：

粗箭头表示兄弟指针，细箭头表示孩子指针。
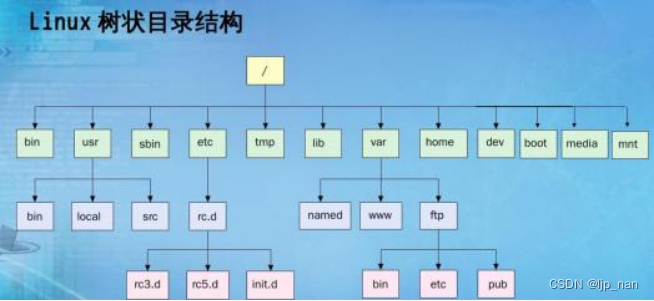
linux目录树

二叉树的概念及结构

二叉树的概念

二叉树是另一种树型结构，它的特点是每个节点至多只有两颗子树（即二叉树中不存在度大于2的节点），并且，二叉树的子树有左右之分，其次序不能任意颠倒。如下图所示：

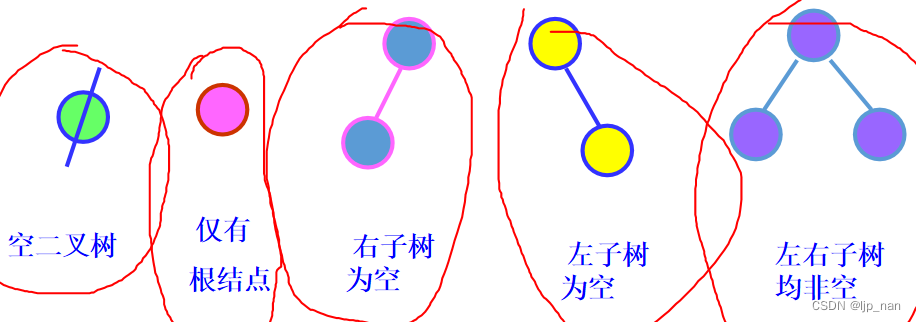
在这里插入图片描述

二叉树有五种形态：空二叉树，只有根节点的二叉树，只有左孩子，只有右孩子，左右孩子都有
如下图所示：

两种特殊的二叉树

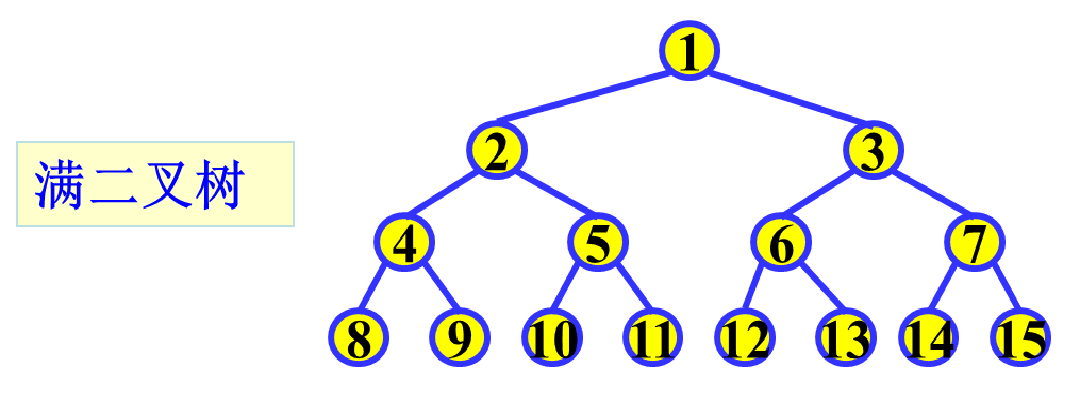
定义：如果一个二叉树深度为K，结点数为2k-1，则称为满二叉树
特点：每一层上的结点数都是最大结点数。
如下图所示：

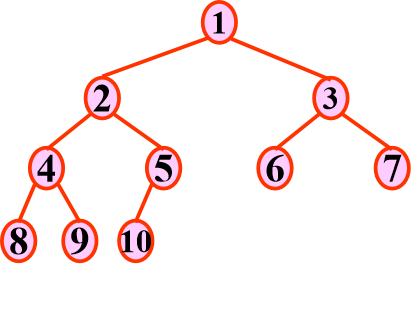
完全二叉树
定义: 指深度为k的，有n个结点的，且每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应。
特点:
1）叶子结点只可能在层次最大的两层上出现；
2）对任一结点，若其右分支下的子孙的最大层次为L，则其左分支下的子孙的最大层次必为L或L+1。
即：完全二叉树可以不满，但是少的结点只能从满二叉树的最下层、最右边少起。
如下图所示:

完全二叉树的节点个数的范围为：
最小： $2^(k-1)$
最大： $2^k-1$

二叉树的存储结构

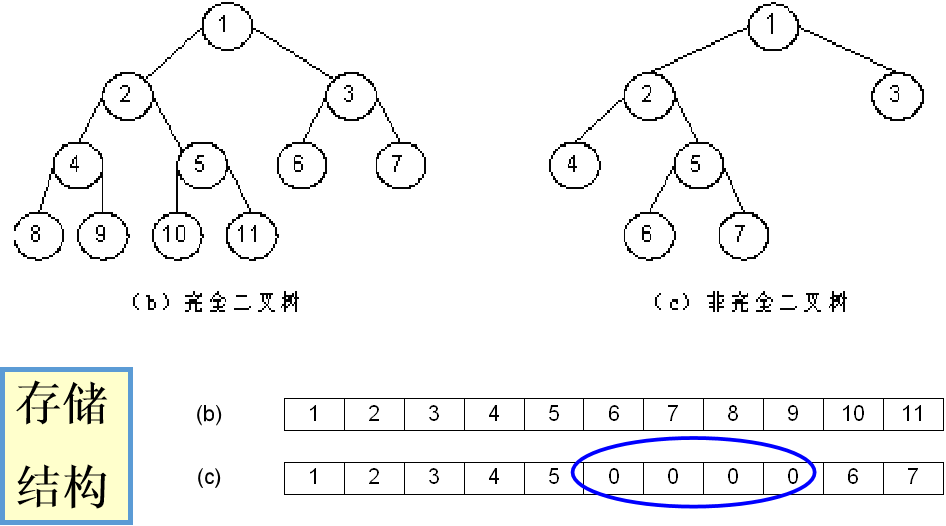
1、顺序存储结构: 用一组连续的存储单元存放二叉树中的结点。
如下图所示：用顺序结构存储的二叉树

优点：适用于满二叉树和完全二叉树，按结点从上至下，从左到右顺序存放，结点序号唯一反映出结点间逻辑关系，又可用数组下标值确定结点位置。
缺点：对一般二叉树，需增加许多空结点将一棵二叉树改造成完全二叉树，浪费大量存储空间。(否则数组元素下标间不能反映各结点间逻辑关系)
父亲和孩子的下标关系
父亲节点 = （child-1)/2
左孩子 = parent * 2 + 1
右孩子 = parent * 2 + 2
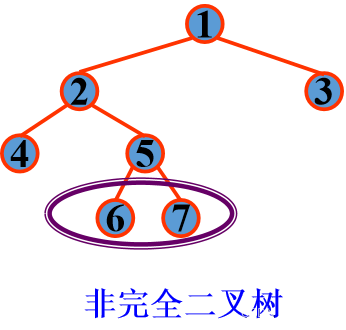
这里需要注意：非完全二叉树是不适合用顺序表存储的，它会造成很多的空间浪费。所以需要用到链式存储结构：
2.链式存储结构：二叉链表：每个结点由数据域、左指针域和右指针域组成。

Typedef struct node{
      Datatype  data;
      Struct node *lchild,*rchild;
}BinNode
//二叉链表的存储结构

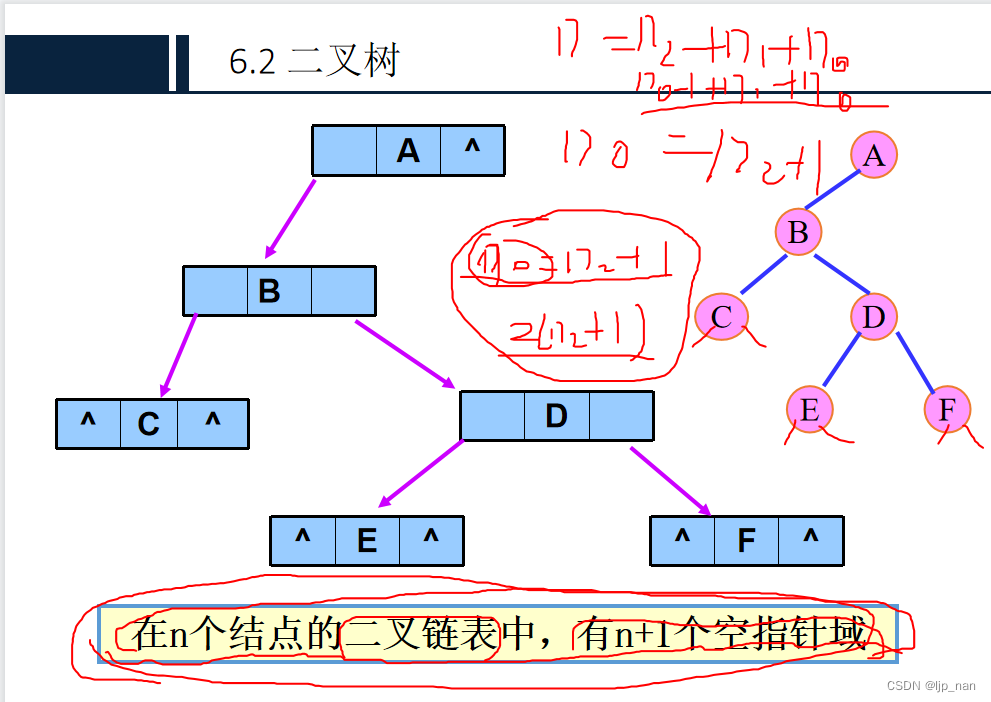
在这里插入图片描述

三叉链表：
三叉链表：增加一个指向其双亲结点的指针域。

堆的概念

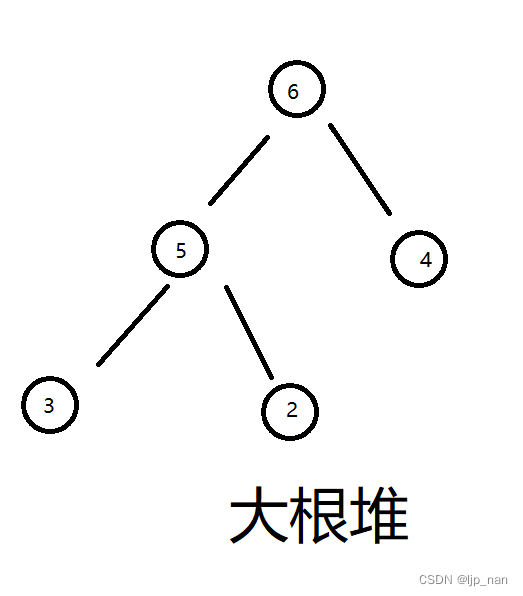
堆的基本概念

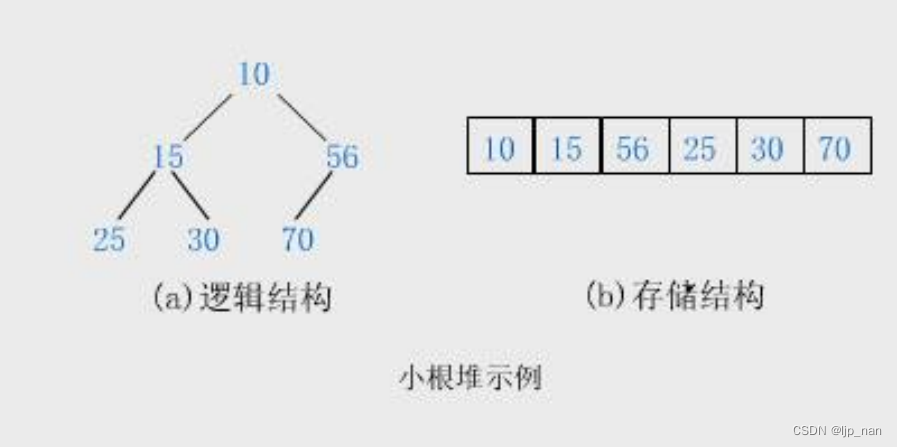
在这里插入图片描述

堆的插入

我们可以利用父亲和孩子在顺序表中的下标关系来建立堆，首先我们插入数据，然后如果建立小堆的话，插入的数据比原来的父亲小就交换父亲和孩子数值的位置。这种算法叫做向上调整算法：
具体的代码实现如下所示：

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
typedef int HPDataType;
//定义存储结构如下：
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;

//接口定义
void HeapInit(HP* php);
void HeapDestory(HP* php);
void HeapPush(HP* php, HPDataType x);

#include "Heap.h"
void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->capacity = php->size = 0;
}
void HeapDestory(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}
void AdjustUp(HP* php, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0) //当child == 0时它没有双亲，也就不需要进行调整了
	{
		if (php->a[child] < php->a[parent])
		{
			//进行交换
			HPDataType tmp = php->a[child];
			php->a[child] = php->a[parent];
			php->a[parent] = tmp;
			//算出上面的双亲节点
			child = parent;
			parent = (child - 1) / 2;
		}
		else  //调整到一半或者已经是堆了就不要调整了。
		{
			break;
		}
	}
}
void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	//首先考虑扩容
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a,sizeof(HPDataType) * newcapacity);
		if (tmp == NULL)
		{
			perror("realloc failed!\n");
			return;
		}
		php->a = tmp;
		php->capacity = newcapacity;
	}
	php->a[php->size] = x;
	php->size++;

	//调整为堆
	//执行向上调整算法
	AdjustUp(php, php->size-1);
}



int main()
{
	HP hp;
	HeapInit(&hp);
	int a[6] = { 70,30,25,56,15,10 };
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		HeapPush(&hp, a[i]);
	}
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		printf("%d ", hp.a[i]);
	}
	HeapDestory(&hp);
	return 0;
}