目录
什么是回溯算法?
基本概念
示例认知
什么时候可以使用回溯算法?
回溯算法经典应用-无向图两节点之间路径
问题描述
回溯过程
代码示例
回溯算法经典应用-四皇后问题
问题描述
四皇后问题解决步骤
Step 1
Step 2
Step 3
Step 4
Step 5
Step 6
Step 7
Step 8
代码示例如何解决四皇后问题
什么是回溯算法?
基本概念
回溯是一种用于寻找某些计算问题的全部(或部分)解的通用算法。
回溯算法的核心思想是逐步构建候选解,如果发现当前构建的候选解不符合要求,就回溯到上一步撤销当前选择,重新选择其他方案,继续构建候选解。这个过程就像是在树形结构中向下逐步探索,到达某个节点时,如果发现无法继续向下搜索,就返回到上一层节点,继续从其他子节点开始探索。
回溯算法通常使用递归实现,每一次递归都对一个子问题进行求解,直到求得最终解或无法继续求解后回溯到上一步。为了避免重复搜索同一个状态,回溯算法通常需要使用状态重置或剪枝等技巧对搜索空间进行优化。
咳咳,说了这么多的理论,其实我的脑子都有点浆糊了,也许能动手的情况下还是少动口是一种好习惯。
下面给大家举例一个生活中最最常见的例子来阐述下这个美丽动人的回溯算法。
示例认知
下面这张图一眼看过去,它是一个有3条路的迷宫。你想知道它是否有出口(为了精确起见,使用你双眼观察法比回溯更有效)。这就是迷宫:
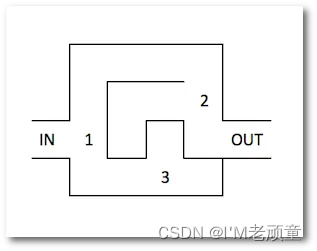
这3条路究竟哪一条才是通往出口的路,或者是没有任何一条可以通往出口呢?我们使用回溯法,将每一条路都尝试走下,当所有的路都走完时,真相就会无所遁形!

上图通过遍历所有的可行路径,当某路不通时返回此路的源点,然后继续搜索可用的路,直到找到正确的出口。
我们的想法是,我们可以使用递归一步一步地构建解决方案;如果在这个过程中我们意识到这将不是一个有效的解决方案,那么我们停止计算该解决方案,并返回到前面的步骤(回溯)。在迷宫的情况下,当我们处于死胡同时,我们被迫走回头路,但在其它情况下,我们可能会在到达之前意识到,我们正在走向一个无效的(或不好的)解决方案。
什么时候可以使用回溯算法?
当我们遇到下面的几种类型时,就可以使用回溯算法来解决
- 决策问题--在这个问题中,我们寻找一个可行的解决方案。
- 优化问题--在这个问题中,我们寻找最优解。
- 枚举问题--在这个问题中,我们找到所有可行的解决方案。
我们平时最为常见的就是解决组合问题、排列问题、迷宫问题、数独问题、四皇后问题、无向图节点路径问题。
然而,它并不是一个优化的算法,因为它的核心使用了暴力方法。因此,如果时间复杂性受到限制,建议使用其他可能更适合这种情况的优化算法。
回溯算法经典应用-无向图两节点之间路径
问题描述
下面是一张无向图,现在我们要计算出从A到E两个节点之前所有可行的路径。需要注意的是在计算有向图中两个顶点之间存在的路时,路径不包含循环,原因很简单,因为一个循环包含无限数量的路径。
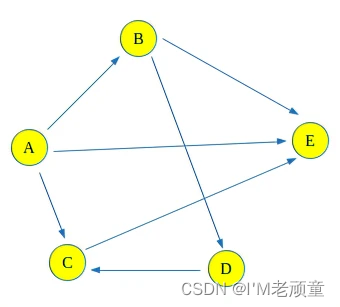
这个问题可以使用回溯来解决,即选择一条路径并开始在其上行走,检查它是否引导我们到达目的地顶点,然后计算路径并回溯到另一条路径。如果路径不指向目标顶点,则丢弃该路径。这种类型的图遍历称为回溯。
回溯过程
上图的回溯过程如下所示(红色顶点为源顶点,淡蓝色顶点为目的顶点,其余为中间路径或丢弃路径)
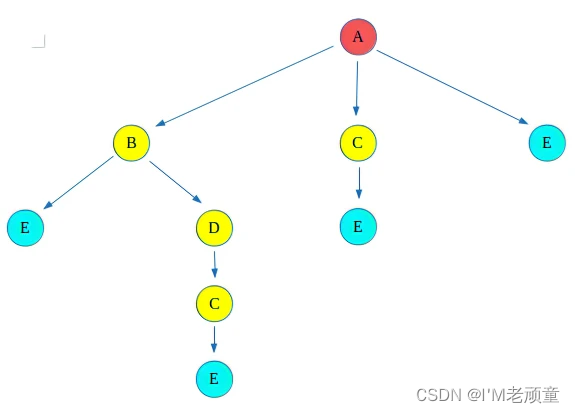
为什么这个解决方案不适用于包含圈的图?下面的这张图为改造后包含循环的图。
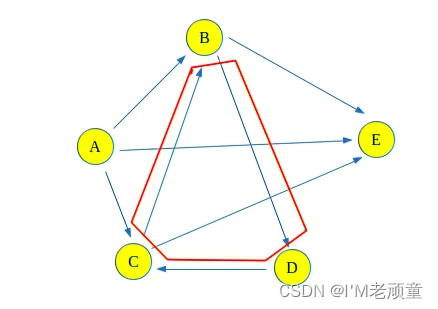
现在如果在C和B之间再增加一条边,就会形成一个循环(B->D->C->B)。因此,在循环的每个循环之后,长度路径将增加,这将被认为是不同的路径,并且由于循环,将有无限多的路径
代码示例
下面我们使用代码示例,逐步的为大家展示整个解决过程。
首先,我们需要定义出无向图中的节点,包括节点之间的关系。
static class Node {
/**
* 节点名称
*/
String name;
/**
* 相邻节点集合
*/
List<Node> adjacentDistance;
public Node(String name) {
this.name = name;
adjacentDistance = new ArrayList<>();
}
/**
* 添加相邻节点
* @param node 相邻节点
*/
public void addEdge(Node node) {
this.adjacentDistance.add(node);
}
@Override
public String toString() {
return "Node{"+this.name+"}";
}
}下面我们把无向图中所有节点以及节点之间的关系全部构建出来。
public static List<Node> buildNodeList() {
List<Node> nodes = Arrays.asList(
new Node("A"),//0
new Node("B"),//1
new Node("C"),//2
new Node("D"),//3
new Node("E")//4
);
// 添加节点之间的关系
nodes.get(0).addEdge(nodes.get(1));//A-B
nodes.get(0).addEdge(nodes.get(2));//A-C
nodes.get(0).addEdge(nodes.get(4));//A-E
nodes.get(1).addEdge(nodes.get(3));//B-D
nodes.get(1).addEdge(nodes.get(4));//B-E
nodes.get(2).addEdge(nodes.get(0));//C-A
nodes.get(2).addEdge(nodes.get(4));//C-E
nodes.get(3).addEdge(nodes.get(2));//D-C
return nodes;
}下面我们就编写回溯算法,来计算A-E节点之间所有可行的路径。代码逻辑实现的核心就是使用递归遍历所有节点,然后找到符合条件的节点。
public static List<String> path(Node start, Node end, String path) {
List<String> paths = new ArrayList<>();
// 如果起始节点和终止节点相同,直接返回起始节点
if (start == end) {
paths.add(start.name);
return paths;
}
// 将当前节点添加到路径上
path += start.name + " -> ";
// 遍历当前节点的相邻节点
for (Node node : start.adjacentDistance) {
// 如果相邻节点就是终止节点,将路径添加到结果列表
if (node == end) {
paths.add(path + end.name);
}
// 如果相邻节点不在路径上,递归遍历该相邻节点
else if (!path.contains(node.name)) {
paths.addAll(path(node, end, path));
}
}
return paths;
}
最后使用main方法运行结果
public static void main(String[] args) {
// 构造节点列表
List<Node> nodes = buildNodeList();
// 查找经过节点A和节点E的路径
List<String> paths = path(nodes.get(0), nodes.get(4), "");
// 打印所有经过节点B和节点C的路径
for (String path : paths) {
System.out.println(path);
}
}输出结果为:
A -> B -> D -> C -> E
A -> B -> E
A -> C -> E
A -> E回溯算法经典应用-四皇后问题
问题描述
什么是四皇后问题呢?如果你有一个4*4的棋盘,你需要在棋盘上放置4个皇后。皇后有能力攻击与之在同一行、同一列或同一对角线上的其它皇后。(后宫生存法则)so,每个皇后必须得有自己独立的势力范围,皇后的威严不容侵犯。同理N皇后的问题也是一样在N * N
对于如何排放皇后,我们有两种可能的解决方案。它们如下所示。
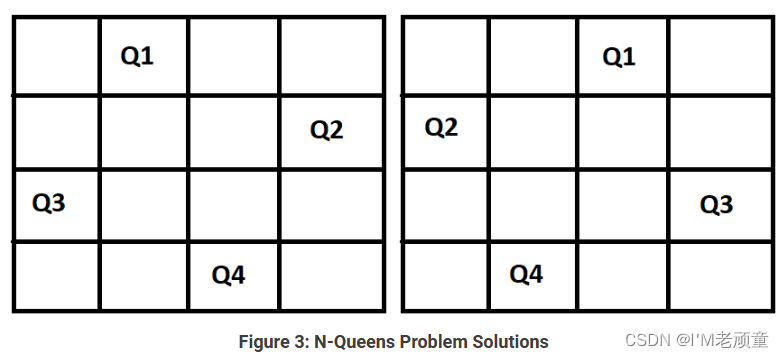
四皇后问题解决步骤
上面己经给出了具体的四皇后的摆放位置 ,但是我们只知道结果,不知道具体的执行过程,下面我们将会一步一步的演示下如何得出这个结果,让大家知其然,知其所以然。
Step 1
我们先将将女王1号放在一个安全不被攻击的位置。因为棋盘上现在没有任何的女王,所以我们可以把女王1号放在任何地方。如下所示:

Step 2
现在,将女王2号放在一个不会受到攻击的位置。
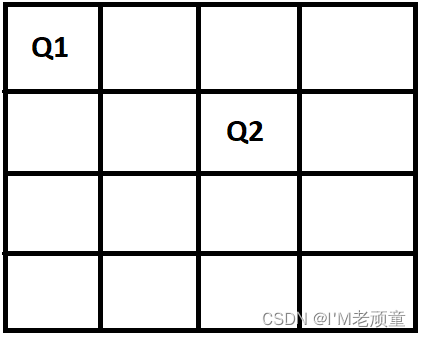
Step 3
好了,大家仔细看上面的图,你会发现我们不可能在不被另外两个女王攻击的情况下将女王3放在第三排。放在第三排的任何位置都会和其它的两个皇后在同一行,同一列,或对角线。这该怎么办呢?下面就该我们的回溯算法发挥其魔力的地方了。
我们后退一步,检查是否可以更改前面的步骤以获得解决方案。所以,我们回溯并改变了女王2的位置,这样它就不会受到任何其他女王的攻击。如下图所示:
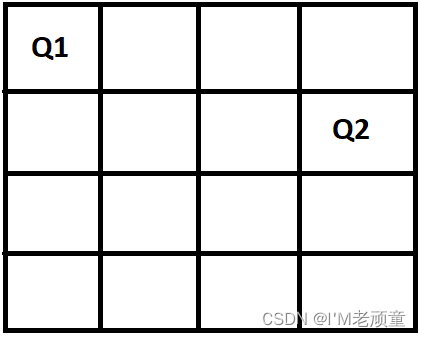
Step 4
经过了下面的调整,我们现在可以将皇后3放在一个不被攻击的位置,如下图所示:
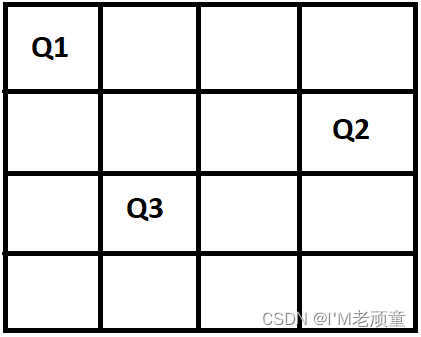
Step 5
大家仔细观察下上面的图,你会注意到我们不能在第四排的任何地方放置女王4而不受到其他三个女王的攻击。
所以,继续回溯!回到过去!试着改变女王3的位置。但女王3已经别无选择了。我们不能把女王3放在其他任何地方而不被另外两个女王攻击。
继续回溯!再次倒退,并试图改变女王2的位置。但很可惜,女王2也已经没有选择了。Oh, God !
继续回溯!所以再次退回并改变女王1的位置。我们只有一样不断的一步一步的回溯,不断的做出选择,直到找到一种新的解决方法。
所以我们现在调整女王1的位置,如下图所示:

Step 6
继续将女王 2号摆放到一个不被其它女王攻击的位置 ,如下图所示:

Step 7
我们继续将女王 3号摆放到一个不被其它女王攻击的位置 ,如下图所示:
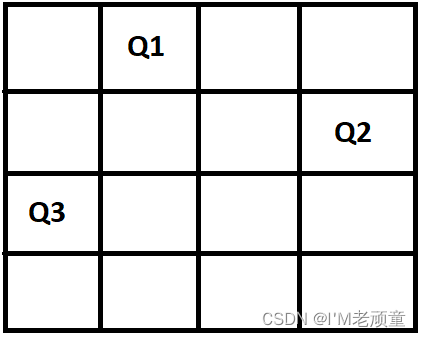
Step 8
最后我们将女王 4号摆放到一个不被其它女王攻击的位置 ,成功就在眼前!如下图所示:
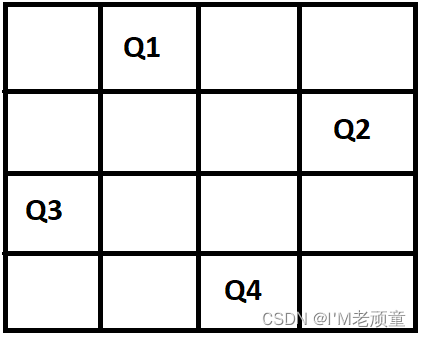
OK,经过我们的不断的回溯不断的尝试,终于找到了解决方案。当然大家如果继续回溯,继续寻找,也可以寻找出另外一种解决方案,这里不在赘述,大家自行尝试即可。
通过上面的演示推理,相信大家对于回溯算法己经有了一个较为深刻的认识了吧。
下面我们通过使用代码的方式,来实现这个四皇后以及N皇后的问题。通过代码的运行,相信大家对于回溯算法一定可以更加熟悉和掌握它。
代码示例如何解决四皇后问题
我们首先分析下代码思路
- 首先需要定义常量用来皇后在棋盘中的位置。在这里我们使用一个组数来保存皇后的位置,如position[0] =1 表示皇后在第1行的第2列
- 然后我们不断的尝试将皇后放在 每一行,每一列的位置,判断是否满足条件,如果不满足则回溯到上一步,更改皇后的位置,直到找到满足条件的位置。
- 判断皇后是否在同一行,同一列,对角线,具体的判断方法详见代码。
代码如下:
public class FourQueens {
public static void main(String[] args) {
solution();
}
//定义一个变量表示棋盘的大小为4,修改n的值即可改变棋盘的大小
public static int n = 4;
// position用于保存每一行中皇后的位置
public static int[] position = new int[n];
// 皇后问题求解函数
public static void solution(){
// 调用回溯算法函数,参数0表示从第0行开始进行回溯
backtrack(0);
}
// 回溯算法函数
public static void backtrack(int row) {
// 递归结束条件
if (row == n){
// 如果所有的皇后放置完毕,输出结果
printResult();
return;
}
// 枚举第row行的所有可能位置
for (int i = 0; i < n; i++) {
// 如果当前位置可用
if (checkPosition(row,i)){
// 在当前位置放置皇后
position[row] = i;
// 继续向下一行进行回溯
backtrack(row +1);
}
}
}
// 判断位置是否合法
public static boolean checkPosition(int row ,int col) {
// 遍历前面每行是否冲突
for (int i = 0; i < row; i++) {
// 检查是否在同一列或者是否在对角线上
if (position[i] == col || Math.abs(i - row) == Math.abs(position[i] - col)){
// 如果在同一列或者对角线上,返回false
return false;
}
}
// 如果当前位置与前面已放置皇后的位置不冲突,则返回true
return true;
}
// 打印当前皇后的位置
public static void printResult() {
// 打印分割线
System.out.println("-----------------------");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (position[i] == j){
// 如果该位置有皇后,则输出Q
System.out.print("Q ");
}else{
// 如果该位置没有皇后,则输出"."
System.out.print(". ");
}
}
// 打印换行符
System.out.println();
}
}
}如果大家对四皇后的分析己经理解的话,那么代码也是非常通俗易懂,就是使用迭代不断的遍历皇后在每一格中的位置,当发现某一格子不满足时在回溯到上一步重新摆放皇后的位置,直到找到满意的位置为止。
好了,回溯算法就为大家介绍到这里,如果大家有什么想法,可以在留言区进行讨论。