数学函数
OpenCL C实现了C99规范中描述的数学函数。使用这些数学函数的应用程序需要在代码中包含math.h头文件。这些数学函数可以作为OpenCL内核的内置函数。
对于表5-2和表5-3中的数学函数,我们将使用泛型类型名gentype指示这些函数可以取float、float2、float3、float4、float8、float16作为参数类型,另外,如果支持双精度扩展,参数类型还可以是double、double2、double3、double4、double8、double16。另外使用泛型类型名gentypei 指示 int、int2、int3、int4、int8、int16数据类型。泛型类型名gentypef指示 float、float2、float3、float4、float8、float16数据类型。泛型类型名gentyped指示double、double2、double3、double4、double8、double16数据类型。
5-2 内置数学函数
gentype acos(gentype x) 计算×的反余弦
gentype acosh(gentype x) 计算×的反双曲余弦
gentype acospi(gentype x) 计算acos(x)/p
gentype asin(gentype x) 计算×的反正弦
gentype asinh(gentype x) 计算×的反双曲正弦
gentype asinpi(gentype x) 计算asin(x)/p
gentype atan(gentype y_over_x) 计算y_over_x的反正切
gentype atan2(gentype y, gentype x) 计算y/x的反正切
gentype atanh(gentype x) 计算×的双曲反正切
gentype atanpi(gentype x) 计算atan(x)/p
gentype atan2pi(gentype y,gentype x) 计算atan2(y,c)/p
gentype cbrt(gentype x) 计算x的立方根
gentype ceil(gentype x) 使用正无穷舍人模式舍入为一个整数
gentype copysign(gentype x,gentype y) 返回×,改变其符号使之与y的符号一致
gentype cos(gentype x) 计算×的余弦
gentype cosh(gentype x) 计算×的双曲余弦
gentype coapi(gentype x) 计算cos(px)
gentype erfc(gentype x) 计算余补误差函数1.0 - erf(x)
gentype erf(gentype x) 计算误差函数。
gentype exp(gentype x) 计算×以e为底的指数
gentype exp2(gentype x) 计算×以2为底的指数
gentype exp10(gentype x) 计算×以10为底的指数
gentype expml(gentype x) 计算e^x-1.0
gentype fabs(gentype x) 计算一个浮点数的绝对值
gentype fdim(gentype x,gentype y) 如果x>y,返回x-y,如果×小于或等于y,则返回+0
gentype floor(gentype x) 使用负无穷舍人模式舍入为一个整数
gentype fma(gentype a, gentype b, gentype c) 将c与a和b的无限精度乘积相加,返回求和结果的正确舍人浮点表示。
不会对中间乘积结果进行舍入。
边界行为遵循IEEE 754-—2008标准
gentype fmax(gentype x, gentype y) 如果x < y,返回y;否则返回x。如果一个参数是NaN, fmax()会返回另一个参数。
gentypef fmax(gentypef x, float y) 如果两个参数都是NaN,fmax()会返回NaN
gentyped fmax(gentyped x, double y)
gentype min(gentype x, gentype y) 如果y<x,返回y;否则返回x。
gentypef fmin(gentypef x, float y) 如果一个参数是NaN,fmin()会返回另一个参数。
gentyped fmin (gentyped x, double y) 如果两个参数都是NaN,fmin()会返回NaN
gentype fmod(gentype x, gentype y) 返回x -y * trunc(x/y)
gentype fract(gentype x, global gentype *iptr) 返回fmin(x - floor (x),0x1.fffffep - 1f)
gentype fract(gentype x, local gentype *iptr) floor()在iptr中返回
gentype fract(gentype x, private gentype *iptr)
gentype frexp(gentype x, global intn *exp) 从×抽取尾数和指数。对于每个分量,返回的尾数是
gentype frexp(gentype x, local intn *exp) 一个浮点数,值为0或介于[1/2,1)之间。x的每个
gentype frexp(gentype x, private intn *exp) 分量等于所返回的尾数*2^exp
gentype hypot(gentype x,gentype y) 计算 x^2+y^2的平方根值(没有过分的上澄出或下隘出)
intn ilogb(gentype x) 将x的指数作为整数值返回
gentype ldexp (gentype x,intn exp) 返回x*2^exp
gentype ldexp (gentype x,int exp)
gentype lgammna(gentype x) 计算log gamma函数
gentype lgamma_r(gentype x, global intn *signp)
gentype lgamna_r(gentype x, local intn*signp)
gentype lganna_r(gentype x,private intn *signp)
gentype log(gentype x) 计算×的自然对数
gentype log2 (gentype x) 计算×的以2为底的对数
gentype log10 (gentype x) 计算×的以10为底的对数
gentype log1p(gentype x) 计算loge(1.0+ x)
gentype logb(gentype x) 计算x的指数,这是loge|x|的整数部分
gentype mad(gentype a, gentype b, gentype c) mad近似a*b+c。对于是否对a*b的乘积舍人以及如何舍入,
以及如何处理不正常的中间乘积结果,这些都未定义。
如果速度比精度更重要,就可以使用mad
gentype maxcmag(gentype x, gentype y) 如果|x|>|y|,返回×;如果|y|>|x|,返回y;否则为fmax(x, y)
gentype minmag(gentype x, gentype y) 如果|x|<|y|,返回x;如果|y|<|×|,返回y;否则为fmin(x,y)
gentype modf(gentype x, global gentype *iptr) 分解一个浮点数。modf 函数将参数×分解为整数部分
gentype modf(gentype x, local gentype *iptr) 和小数部分,它们与参数符号相同。整数部分存储在
gentype modf(gentype x, private gentype *iptr) iptr指向的对象中,小数部分则由函数返回
float nan(uint nancode) 返回一个静默 NaN。nancode可能为返回的 NaN的有效位置
floatn nan(uintn nancode)
double nan(uint nancode)
doublen nan(uintn nancode)
gentype nextafter(gentype x, gentype y) 计算x之后(朝着y的方向)下一个可表示的单精度或双精度浮点值。
因此,如果y小于x, nextafter会返回小于×的可表示的最大浮点数
gentype pow(gentype x, gentype y) 计算×的y次方
gentype pown(gentype x, intn y) 计算x的y次方,y是一个整数
gentype powr(gentype x,gentype y) 计算×的y次方,x ≥ 0
gentype remainder(gentype x, gentype y) 计算值r(r=x-n*y),其中n是最接近x/y准确值的整数。
如果最接近x/y的整数有两个,n取其中的偶数;
如果r为0,则与x符号相同
gentype remquo(gentype x, gentype y, global gentypei *quo) 计算值r(r =x-n*y),其中n是最接近×/y准确值的整数。
gentype remquo(gentype x, gentype y, local gentypei *quo) 如果最接近×/y的整数有两个,n取其中的偶数:
gentype remquo (gentype x, gentype y, private gentypei *quo) 如果r为0,则与×符号相同
这个值与remainder函数的返回值相同。
remquo还会计算x/y整数商的低7位,这个值与x/y符号相同。
这个有符号值存储在quo指定的对象中
gentype rint(gentype x) 舍入为采用浮点格式的整数值〔使用就近舍入模式)
gentype rootn(gentype x,intn y) 计算x的1/y次方
gentype round(gentype x) 返回最接近×的整数值(从0向外舍入),而不考虑当前的舍入方向
gentype rsqrt(gentype x) 计算x平方根的倒数
gentype sin(gentype x) 计算x的正弦
gentype sinoos lgentype x, global gentype *cosval) 计算×的正弦和余弦。计算得到的正弦值作为返回值,
gentype sinoos(gentype x, local gentype *cosval) 计算得到的余弦在cosval中返回
gentype sinoos(gentype x, private gentype *oosval)
gentype sinh(gentype x) 计算×的双曲正弦
gentype sinpi(gentype x) 计算sin(px)
gentype sqrt(gentype x) 计算×的平方根
gentype tan(gentype x) 计算x的正切
gentype tanh(gentype x) 计算×的双曲正切
gentype tanpi(gentype x) 计算tan(px)
gentype tganma(gentype x) 计算 gamma 函数
gentype trune(gentype x) 使用向0舍入模式舍入为整数
内置half_和native_数学函数
gentypef half_cos(gentypef x) 计算×的余弦。x必须在-2^16 ~ +2^16内
gentypef half_divide(gentypef x, gentypef y) 计算x/y
gentypef half_exp(gentypef x) 计算x以e为底的指数
gentypef half_exp2(gentypef x) 计算x以2为底的指数
gentypef half_exp10(gentypef x) 计算×以10为底的指数
gentypef half_1og(gentypef) 计算×的自然对数
gentypef half_log2(gentypef x) 计算x以2为底的对数
gentypef half_1og10 (gentypef x) 计算x以10为底的对数
gentypef half powr(gentypef x, gentypef y) 计算x的y次方,其中x≥0
gentypef half_recip(gentypef x) 计算x的倒数
gentypef half_rsqrt(gentypef x) 计算x的平方根的倒数
gentypef half_sin(gentypef x) 计算x的正弦。x必须在-2^16 ~ +2^16内
gentypef half_sqrt(gentypef x) 计算×的平方根
gentypef half_tan (gentypef x) 计算×的正切。x必须在-2^16 ~ +2^16内
gentypef native_cos(gentypef x) 计算×的余弦,x的范围由实现定义。最大误差也由实现定义
gentypef native_divide(gentypef x,gentypef y) 计算×/y,参数范围由实现定义。最大误差也由实现定义
gentypef native_exp(gentypef x) 计算×以e为底的指数,参数范围由实现定义。最大误差也由实现定义
gentypef native_exp2(gentypef x) 计算×以2为底的指数,参数范固由实现定义。最大误差也由实现定义
gentypef native_exp10(gentypef x) 计算×以10为底的指数,参数范由实现定义。最大误差也由实现定义
gentypef native_log(gentypef x) 计算×的自然对数,参薮范围由实现定义。最大误差也由实现定义
gentypef native_1og2(gentypef x) 计算×以2为底的对数,参数范围由实现定义。最大误差也由实现定义
gentypef native_1og10(gentypef x) 计算x以10为底的对数,参数范围由实现定义。最大误差也由实现定义
gentypef native_recip(gentypef xe) 计算×的倒数,参数范围由实现定义。最大误差也由实现定叉
gentypef native_rsqrt(gentypef x) 计算×平方根的倒数,参数范围由实现定义。最大误差也由实现定义
gentypef native_sin(gentypef x) 计算的正弦,参数范围由实现定义。最大误差也由实现定义
gentypef native_sqrt(gentypef x) 计算×的平方根,参薮范围由实现定义。最大误差也由实现定义
gentypef native_tan(gentypef x) 计算x的正切,参数范围由实现定义。最大误差也由实现定义
除了表5-2中所列的数学函数外,OpenCL C还为单精度浮点标量和矢量数据类型实现了另外两组最常用的数学函数。这些数学函数(见表5-3)是以精确性换取性能,为开发人员提供了选项以便做出适当的选择。这些数学函数可以划分为以下几类:
1)表5-2中带half_前缀的函数子集。这些函数实现的最小精度为10位,也就是说,ulp值≤8192 ulp。
2)表5-2中带native_前缀的函数子集。与不带native_前缀或带half_前缀的相应函数相比,这些函数通常有最佳性能。这些函数的精度(以及有些情况下的输入范围)由具体实现定义。
3)完成以下基本操作的half_和 native_函数:除法和倒数。
浮点常量
可用的常量见表5-4。有_F后缀的常量类型为float,在float类型的精度范围内是精确的。没有_F后缀的常量类型为double,在 double类型的精度范围内是精确的,只有当OpenCL实现支持双精度扩展时才可用。
M_E_F e的值
M_E
M_LOG2E_F log₂e的值
M_LOG2E
M_LOG10E_F lge的值
M_LOG10E
M_LN2_F ln2的值
M_LN2
M_LN10_F ln10的值
M_LN10
M_PI_F π的值
M_PI
M_PI_2_F π/2的值
M_PI_2
M_PI_4_F π/4的值
M_PI_4
M_1_PI_F 1/π的值
M_1_PI
M_2_PI_F 2/π的值
M_2_PI
M_2_SQRTPI_F 2/sqrt(π)的值
M_2_SQRTPI
M_SQRT2_F sqrt(π)的值
M_SQRT2
M_SQRT1_2_F 1/sqrt(π)的值
M_SQRT1_2
相对误差作为ulp
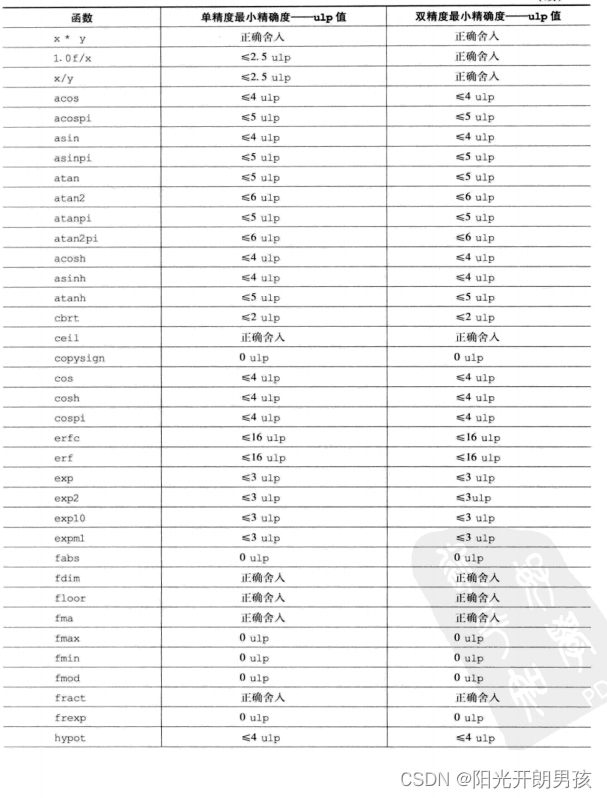
表5-5给出了单精度和双精度浮点基本运算和函数的最大相对误差(定义为ulp,即最后一位的单位数)。ulp定义如下:
如果x是介于两个有限连续浮点数α和b之间的一个实数,但不等于α和b,那么ulp(x) = | b-a |;否则,ulp(x) 是最靠近x的两个不相等有限浮点数之间的距离。另外,ulp(NaN)为NaN。
基本运算和内置数学函数的ulp值
表5-5给出了单精度和双精度浮点基本运算和函数的最大相对误差(定义为ulp,即最后一位的单位数)。ulp定义如下:
如果x是介于两个有限连续浮点数a和b之间的一个实数,但不等于a和b,那么ulp(x)= |b-a|;否则,ulp(x)是最靠近x的两个不相等有限浮点数之间的距离。另外,ulp(NaN)为NaN。

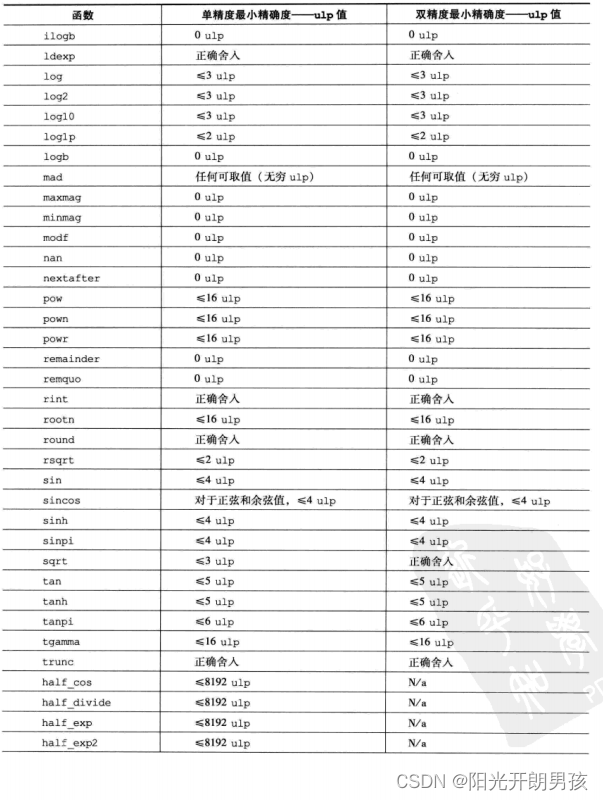
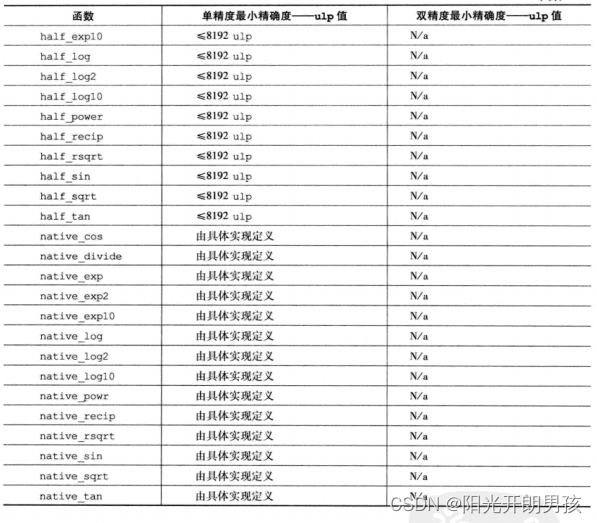
下面的列表进一步澄清了ulp值和舍入模式行为:
1)就近舍入模式是完全简档的默认舍入模式。对于嵌入式简档,默认舍入模式可以是向0舍入或就近舍入。如果 CL_DEVICE_SINGLE_FP_CONFIG中支持CL_FP_ROUND_TO_NEAREST,则嵌入式简档支持就近舍入作为默认舍入模式;否则,默认舍入模式为向0舍入。
2)0 ulp用于不需要舍入的数学函数。
3)内置数学函数lgamma和 lgamma_r的ulp值目前未定义。