💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码、Simulink、文章讲解
💥1 概述
文献来源:

抗扰PID控制,英文名为Disturbance Rejection Proportional-Integral-Derivative control, 简称DR-PID,是一种基于自抗扰控制原理设计的先进PID控制方法[1]。抗扰PID控制器采用了经典PID形式和自抗扰控制器设计方法,参数调节简单、适用范围广、鲁棒性强,其调节方法与PID工程调参经验兼容。
该文针对一类相对阶次的最小相电厂,提出了一种新的抗扰比例-积分-微分(DR-PID)方案。本文首次阐明并阐明了隐藏在PID控制结构中的本质主动抗扰(ADR)机制。在改进扰动观测器的基础上推导了DR-PID方案,将主动抗扰机制无缝嵌入经典PID结构中。这种DR-PID方案在典型的两自由度控制结构中实现,该结构包含一个标准PID控制器和一个预滤波器。根据鲁什定理对闭环极点进行研究,建立了内部稳定性条件。随之而来的内部稳定性条件为DR-PID设计提供了有效的指导,DR-PID具有无限的增益裕量和最少的工厂信息。通过五次数值比较来说明新的DR-PID方案的有效性。所提出的DR-PID方案的物理可实现性也通过磁悬浮系统的实验得到证明。
原文摘要:
In this paper, a new disturbance rejection proportional–integral–derivative (DR-PID) scheme is proposed for a class of minimum phase plants with low relative order. The essential active disturbance rejection (ADR) mechanism that is otherwise hidden in PID control structure has been illuminated and clarified in this paper for the first time.The proposed DR-PID scheme is derived on the basis of a modified disturbance observer to embed the active disturbance rejection mechanism seamlessly in the classical PID structure. Such a DR-PID scheme is implemented in a typical two-degree-of-freedom control structure that contains a standard PID controller and a pre-filter. The internal stability condition is established by investigating the closed-loop poles according to Rouche’s theorem. The ensuing internal stability condition provides effective guidelines for DR-PID design that has infinite gain margin with minimum plant information. Five numerical comparisons are performed to illustrate the effectiveness of the new DR-PID scheme. The physical realizability of the proposed DR-PID scheme is also demonstrated by experiments on a magnetic levitation system.
经典的比例-积分-微分(PID)控制器因其简单性和鲁棒性而成为工业工程中使用最广泛和最成功的控制器。尽管在过去的几十年中已经提出了富有成效的现代控制理论,但PID控制器及其变体继续在过程控制中超过90%的控制回路中占据主导地位[1],[2],[3],[4],[5],[6],[7],[8].已经提出了一些著名的调谐规则来增强PID控制器的控制性能[9],[10],[11],[12],[13],[14],[15],[16],[17],[18],[19],[20],它们包括齐格勒-尼科尔斯 (ZN) 调谐规则 [9]、[10]、[13]、直接合成 (DS) 方法 [15]、[16]、[17]、[18] 和内部模型控制 (IMC) 方法 [19]、[20]、[21]、[22], [23]。IFAC第三届PID控制进展会议报告了最新进展[3],[2]。
许多研究集中在控制理论和工程背景下的PID控制,但PID控制中性能调整的原理仍不清楚。例如,1)PID中的积分作用可以消除稳态误差并抑制干扰,但实践经验告诉我们,由于控制器整定中的所有参数都是耦合的,因此仅整定积分参数很难提高控制性能;2)作为一种误差驱动的方法,PID控制仍然需要丰富的工厂信息进行高级控制。实际上,只有少量的工厂信息对于控制器设计至关重要,例如相对阶数和高频增益。如何利用这些有限的工厂信息来提高PID控制性能仍然未知。
对于许多过程控制应用,抗扰性能比纯粹的设定点跟踪更重要。因此,已经提出了一些改进的PID控制器,称为干扰抑制PID(DR-PID),以提高控制性能,并假设工厂模型是确切已知的[24],[25],[26],[27],[28]。灵敏度函数分析是设计抗扰控制器的一种方便的经典技术。

📚2 运行结果


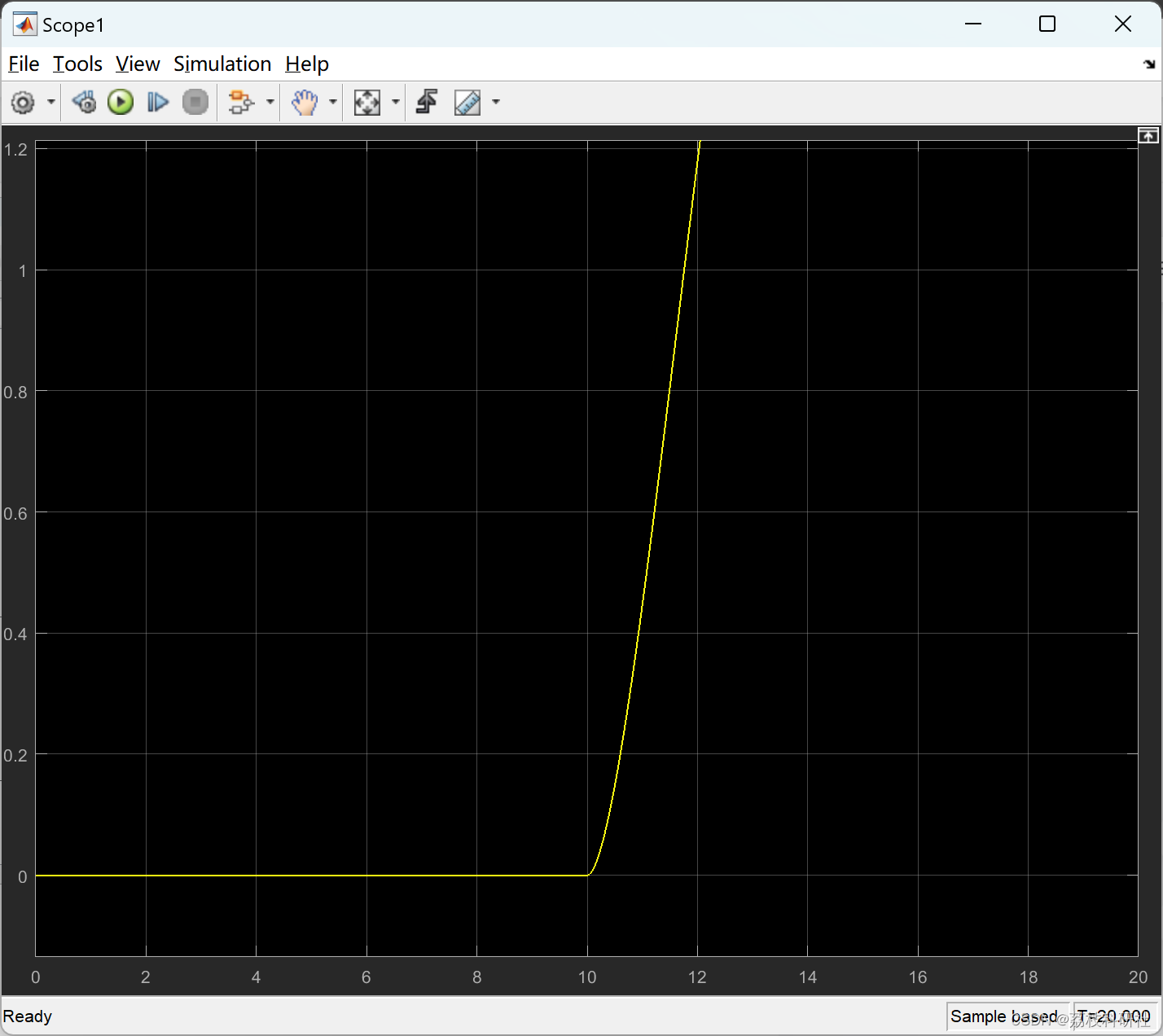
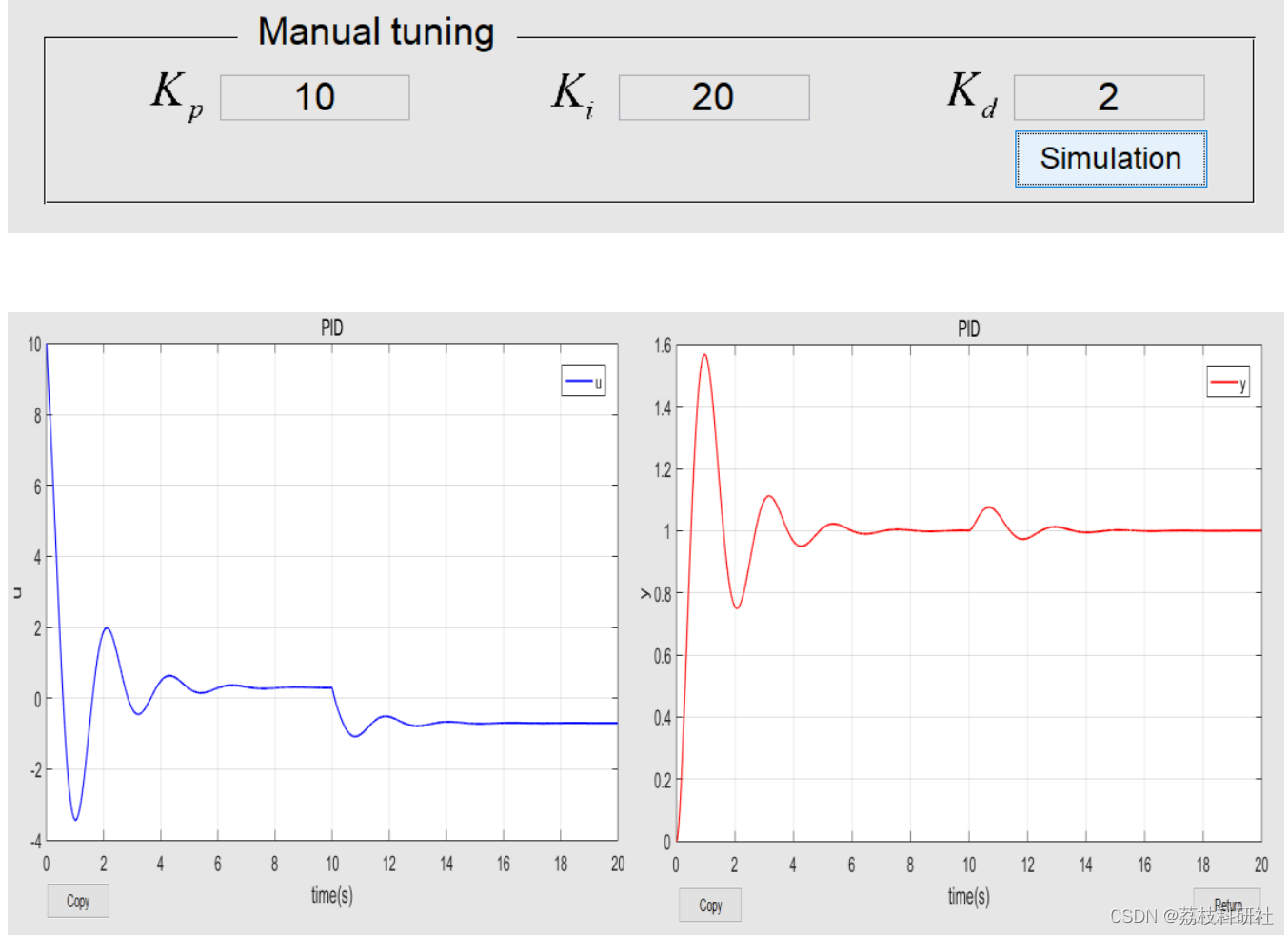
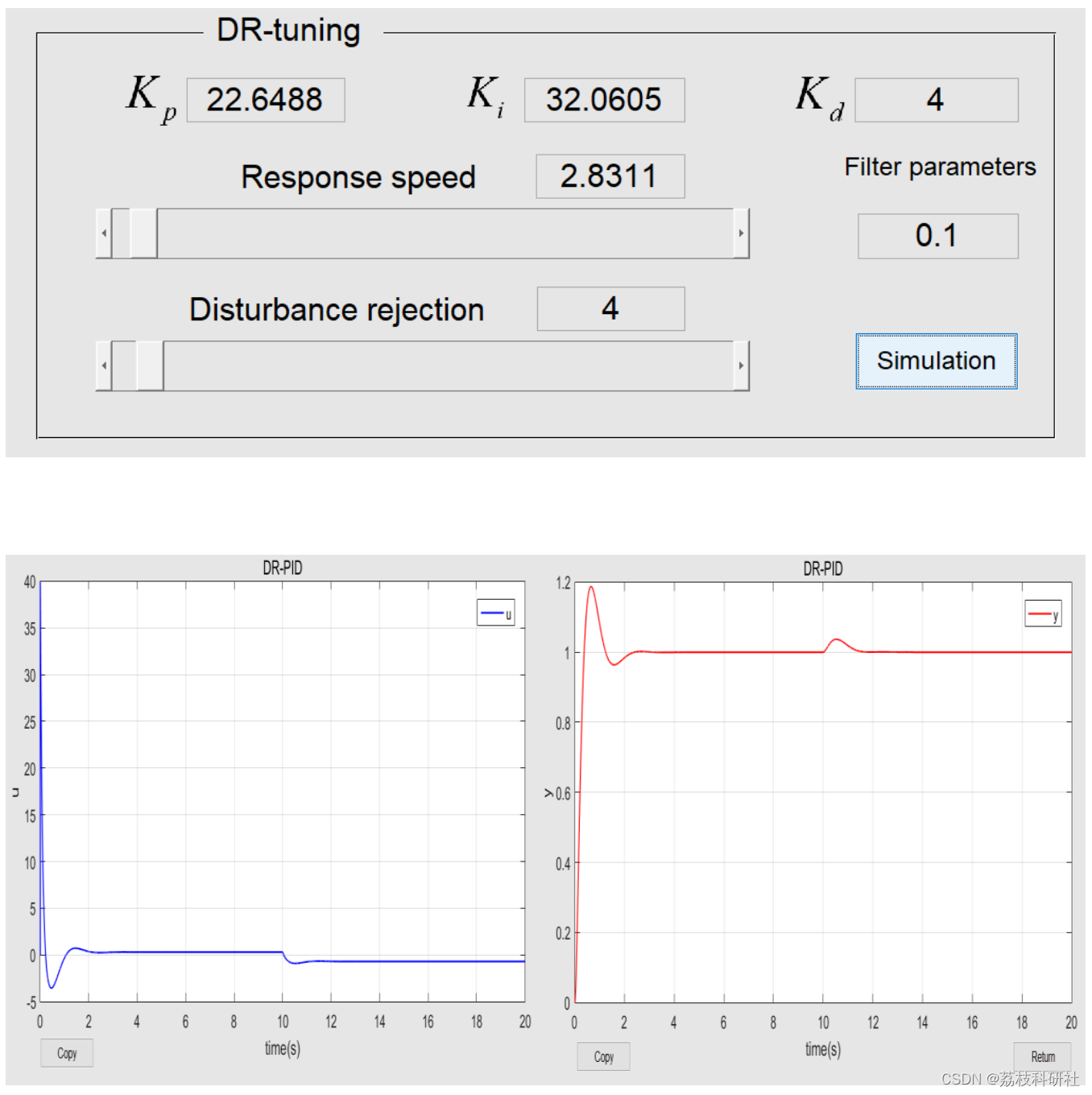

🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1] Nie Zhuoyun, Zhu Chao, Wang Qingguo, Gao Zhiqiang, Shao Hui, Luo Jiliang. Design, analysis and application of a new disturbance rejection PID for uncertain systems. ISA Transactions, 2020. Volume 101, June 2020, Pages 281-294 https://doi.org/10.1016/j.isatra.2020.01.022.
[2] Nie Zhuoyun, Wang Qing-Guo, She Jinhua, Liu Rui-Juan, Guo Dong-Sheng. New results on the robust stability of control systems with a generalized disturbance observer. Asian Journal of Control, 2019; DOI: 10.1002/asjc.2188
[3] Gao Zhiqiang. Scaling and bandwidth-parameterization based controller tuning. Proceedings of 2003 American Control Conference. St Louis, USA: IEEE Press, 2003:4989-4996.
[4] 李高铭,聂卓赟,李兆洋,罗继亮,詹瑜坤. 非平衡负载下轮式移动机器人的抗扰 PID
控制.控制理论与应用, 2020.