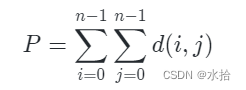回溯的时间复杂度计算

计算回溯时间复杂度，我们可以使用如下公式：答案个数（叶子节点个数）×路径长度（搜索深度）

示例1：77.组合

void backtracking(vector<int>&path,vector<vector<int>>result,int n,int k,int startIndex){
    //终止
    if(path.size()==k){
        result.push_back(path);
        return;
    }
    //单层递归
    for(int i = startIndex;i<=n - (k - path.size()) + 1;i++){
        //加入路径
        path.push_back(i);
        //找到i开头的所有组合 12 13 14
        backtracking(path,result,n,k,i+1);
        //回溯,去掉1开始找2开头的，如果传入startIndex+1那么找2开头的就会出问题了
        path.pop();
    }
    return;
}
vector<vector<int>> combine(int n, int k) {
	vector<int>path;
    vector<vector<int>>result;
    int startIndex = 1;
    backtracking(path,result,n,k,startIndex);
    return result;
}

这道组合题目中，叶子节点个数也就是答案个数为 $C_n^k$ ，搜索深度为k（因为需要k个数字），所以时间复杂度为k* $C_n^k$

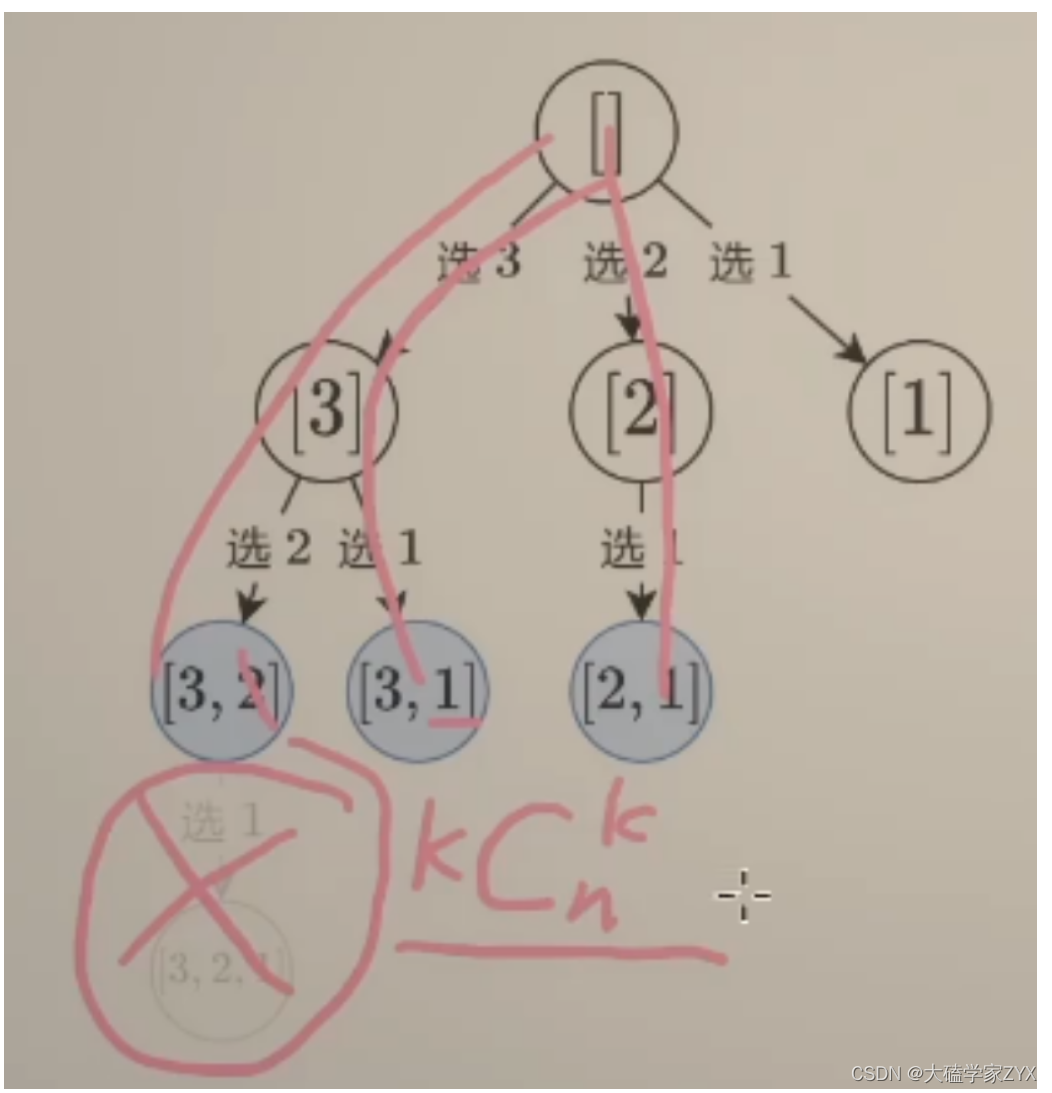
在这里插入图片描述
严格来说，这个公式并不总是对所有回溯问题都适用。因为回溯问题的时间复杂度通常要考虑所有可能的搜索路径，而不仅仅是最终结果（叶子节点）。对于某些问题，可能存在大量的无效路径（即那些未导致有效解的路径），这些路径也会消耗计算资源。

在这个特定的问题中，这样做是正确的，因为每个搜索路径都直接对应一个结果，即从n中选取k个数的组合。所以在这个特定的场景下，可以将时间复杂度描述为k* $C_n^k$ 。但这种描述方法并不总是适用于所有的回溯问题。

示例2：216.组合总和Ⅲ

void backtracking(vector<int>& path,vector<vector<int>>&result,int k,int targetSum,int sum,int startIndex){
    //终止条件
    if(path.size()==k){
        //检查和是否符合要求
        if(sum==targetSum){
            result.push_back(path);
        }
        return;
    }
    
    //单层搜索
    for(int i=startIndex;i<=9;i++){
        //本层累加
        sum = sum+i;
        path.push_back(i);
        //递归for循环，取了[1]之后再取[1,2][1,3][1,4]……
        backtracking(path,result,k,targetSum,sum,i+1);
        //回溯,开始取[2],后面[2,3][2,4]……
        path.pop_back();
        sum = sum-i;
    }

}

//主函数，传参和赋初值可以先写
vector<vector<int>> combinationSum3(int k, int n) {
	int sum=0;
    int startIndex=1;
    vector<int>path;
    vector<vector<int>>result;
    backtracking(path,result,k,n,sum,startIndex);
    return result;
}

这个例子是寻找所有和为特定值n的、长度为k的、元素从1到9的组合。根据题目条件，元素是不可重复的，且每个组合中元素无序。

在这种情况下，我们仍然可以使用公式来大致评估时间复杂度，但需要注意，这只是一个大概的评估，因为在某些路径中，可能由于和超过了目标值或者元素数量已满，提前结束了搜索。

首先，答案个数是不能确定的，这是因为并非所有长度为k的组合的和都会等于n。所以在这种情况下，答案个数（叶子节点数量）并不能提前确定。

然后，每一次选择元素，也就是搜索路径的深度，我们知道是k。

所以在这种情况下，我们并不能准确地得到时间复杂度是多少。我们只能说，时间复杂度的上界是 $O(9^k)$ ，这是因为每一次选择都有9种可能（实际上随着选择的进行，可能的选择数量会越来越少，所以这只是一个上界），我们需要做k次选择。

实际的时间复杂度可能会低于这个上界，因为并非所有可能的路径都会被完全搜索，一旦发现当前路径不可能达到目标，搜索就会被提前终止。但在最坏的情况下，时间复杂度的上界是 $O(9^k)$ 。

示例3：17.电话号码字母组合

class Solution {
public:
//注意数组的初始化方式
    string letterMap[10]={
        "", //是逗号不是分号
        "",
        "abc",
        "def",
        "ghi",
        "jkl",
        "mno",
        "pqrs",
        "tuv",
        "wxyz",
    };
    void backtracking(string path,vector<string>&result,int index,string digits){
        //终止条件
        if(path.size()==digits.size()){
            result.push_back(path);
            return;
        }
        //单层搜索,先得到第一个遍历的数字
        int digitsNum = digits[index]-'0';
        //第一个遍历的数字的字符串
        string a = letterMap[digitsNum];
        for(int i=0;i<a.size();i++){
            path.push_back(a[i]);
            backtracking(path,result,index+1,digits);
            //递归收集'a'开头结束之后，去找'b'开头
            path.pop_back();//pop里面没有参数，error: too many arguments to function call, expected 0, have 1
        }
    }
    vector<string> letterCombinations(string digits) {
        int index=0;
        vector<string>result;
        string path;
        if(digits.size()==0){
            return result;
        }
        backtracking(path,result,index,digits);
        return result;
    }
};

公式计算时间复杂度的方式，需要知道答案个数（叶子节点个数）和路径长度（搜索深度）。

在这个问题中，路径长度即为输入的数字字符串的长度。然而，答案个数则会根据输入的数字字符串的内容变化。假设输入的数字字符串为d1d2d3…dn，每个数字di可以表示的字母个数为ci，那么答案个数就是c1c2c3…*cn。

所以，如果用公式，这个问题的时间复杂度为O(n * c1*c2*c3...*cn) = O(n * C)，其中n是输入的数字字符串的长度，C是答案个数。

另一种考虑方式是，每一位数字都有至多4种可能的字母（例如7和9所对应的字母），所以在最坏情况下，时间复杂度是O(4^n)，因为每一位数字都需要遍历其所有可能的字母。

所以，两种方式得到的时间复杂度都是在同一个数量级上的，都是指数级别的时间复杂度，只是在常数因子上有所不同。这是由于回溯问题的搜索空间通常是指数级别的。

关于剪枝对时间复杂度的影响

从理论上来说，剪枝并不会改变时间复杂度。但在实际执行时，剪枝可以显著减少算法的执行时间。

因为在计算时间复杂度时，我们通常会考虑最坏的情况。例如组合问题，无论是否剪枝，最坏情况下的时间复杂度仍然是k* $C_n^k$ 。

这是因为剪枝并没有改变最坏情况下需要尝试的可能组合的数量。剪枝只是在实际执行时减少了一部分无效的尝试，但并没有改变最坏情况下的搜索空间大小。

回溯的剪枝操作必要性及适用场景

回溯的剪枝操作是非常必要的，很多回溯题目不剪枝很容易tle也就是超时。但是有些题目可以剪枝，有的题目并不能剪枝。

剪枝的可能性并非完全依赖于问题是组合问题还是子集问题。剪枝主要依赖于能否在搜索过程中提前知道某条路径不可能导向一个有效的解，从而在这条路径上不再进行进一步的搜索。

对于子集问题，通常情况下我们需要考虑集合的所有子集，因此通常情况下我们不能提前知道哪些路径不可能导向有效的解，所以通常情况下子集问题不适用于剪枝。例如电话号码这道题。

但也并非绝对，比如有一些子集问题可能会带有额外的约束条件，这些约束条件可能使得一些路径可以被提前判定为不可能导向有效解，此时就可以进行剪枝。

对于组合问题，由于通常我们需要在集合中选取特定数量的元素，所以当剩余的元素不足以达到这个数量时，我们可以判定这条路径不可能导向有效解，因此可以进行剪枝。

示例1：组合剪枝

不剪枝的版本会尝试所有的可能组合，直到得到长度为k的组合。然而，对于一些情况，当我们已经选择了足够多的元素，使得剩余的元素不足以填满长度为k的组合时，我们仍然会继续尝试，这其实是无效的。

剪枝的版本通过减少这些无效的尝试，提高了算法的效率。我们可以提前判断剩余的元素是否足以填满长度为k的组合，如果不足，则提前结束当前的循环，避免无效的尝试。

void backtracking(vector<int>&path,vector<vector<int>>result,int n,int k,int startIndex){
    //终止
    if(path.size()==k){
        result.push_back(path);
        return;
    }
    //单层递归
    for(int i = startIndex;i<=n - (k - path.size()) + 1;i++){
        //加入路径
        path.push_back(i);
        //找到i开头的所有组合 12 13 14
        backtracking(path,result,n,k,i+1);
        //回溯,去掉1开始找2开头的，如果传入startIndex+1那么找2开头的就会出问题了
        path.pop();
    }
    return;
}
vector<vector<int>> combine(int n, int k) {
	vector<int>path;
    vector<vector<int>>result;
    int startIndex = 1;
    backtracking(path,result,n,k,startIndex);
    return result;
}

剪枝优化点：

for(int i = startIndex;i<=n - (k - path.size()) + 1;i++);//优化for的结束条件，当剩余元素不足k的时候直接结束循环

示例2：组合剪枝

//注意剪枝的同时，直接返回，必须要剪枝同时把回溯也做了
void backtracking(vector<int>& path,vector<vector<int>>&result,int k,int targetSum,int sum,int startIndex){
    //终止条件
    if(path.size()==k){
        //检查和是否符合要求
        if(sum==targetSum){
            result.push_back(path);
        }
        //==k无论如何都会return
        return;
    }
    
    //单层搜索
    for(int i=startIndex;i<=9-(k-path.size())+1;i++){
        //本层累加
        sum = sum+i;
        path.push_back(i);
        
        //如果此时的sum已经比targetSum要大，那么已经可以剪枝去找下一个了
        if(sum>targetSum){
            //剪枝，剪枝的时候一定要记得回溯！
            sum = sum-i;
            path.pop_back();
            //这里最好还是写continue，跳过for循环剩下所有部分进行下一次for循环
            continue;
        }
        
        //递归for循环，取了[1]之后再取[1,2][1,3][1,4]……
        backtracking(path,result,k,targetSum,sum,i+1);
        //回溯,开始取[2],后面[2,3][2,4]……
        path.pop_back();
        sum = sum-i;
    }

}

//主函数，传参和赋初值可以先写
vector<vector<int>> combinationSum3(int k, int n) {
	int sum=0;
    int startIndex=1;
    vector<int>path;
    vector<vector<int>>result;
    backtracking(path,result,k,n,sum,startIndex);
    return result;
}

剪枝优化点：

终止条件剪枝：

    //终止条件
    if(path.size()==k){
        //检查和是否符合要求,已经大于sum了就没必要继续找了
        if(sum==targetSum){
            result.push_back(path);
        }
        //==k无论如何都会return
        return;

for循环剪枝

for(int i=startIndex;i<=9-(k-path.size())+1;i++)

示例3：不能剪枝的情况

本题没有剪枝操作，是因为在这个问题中，不存在无效的搜索路径。在组合或者排列问题中，我们使用剪枝来排除那些我们已经知道不可能产生有效答案的搜索路径，以此来优化我们的算法。但在电话号码的字母组合问题中，所有的路径都可能产生有效答案，我们无法提前知道哪些路径是无效的。

在电话号码的字母组合问题中，我们需要为输入的每一个数字选择一个字母，每一个数字都有几个可能的字母，我们需要尝试所有的可能选择，以生成所有可能的组合。

所以，这个问题没有剪枝，并不是因为这个问题是子集问题还是组合问题，而是因为在这个问题中，所有的路径都可能产生有效答案，我们没有办法提前知道哪些路径是无效的，也就无法进行剪枝。

class Solution {
public:
//注意数组的初始化方式
    string letterMap[10]={
        "", //是逗号不是分号
        "",
        "abc",
        "def",
        "ghi",
        "jkl",
        "mno",
        "pqrs",
        "tuv",
        "wxyz",
    };
    void backtracking(string path,vector<string>&result,int index,string digits){
        //终止条件
        if(path.size()==digits.size()){
            result.push_back(path);
            return;
        }
        //单层搜索,先得到第一个遍历的数字
        int digitsNum = digits[index]-'0';
        //第一个遍历的数字的字符串
        string a = letterMap[digitsNum];
        for(int i=0;i<a.size();i++){
            path.push_back(a[i]);
            backtracking(path,result,index+1,digits);
            //递归收集'a'开头结束之后，去找'b'开头
            path.pop_back();//pop里面没有参数，error: too many arguments to function call, expected 0, have 1
        }
    }
    vector<string> letterCombinations(string digits) {
        int index=0;
        vector<string>result;
        string path;
        if(digits.size()==0){
            return result;
        }
        backtracking(path,result,index,digits);
        return result;
    }
};