题目描述

LQ 国拥有 n 个城市, 从 0 到 n−1 编号, 这 n 个城市两两之间都有且仅有 一条双向道路连接, 这意味着任意两个城市之间都是可达的。每条道路都有一 个属性 D, 表示这条道路的灰尘度。当从一个城市 A 前往另一个城市 B 时, 可 能存在多条路线, 每条路线的灰尘度定义为这条路线所经过的所有道路的灰尘 度之和, LQ 国的人都很讨厌灰尘, 所以他们总会优先选择灰尘度最小的路线。
LQ 国很看重居民的出行环境, 他们用一个指标 P 来衡量 LQ 国的出行环 境, PP定义为:

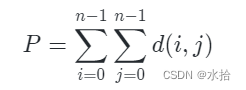
其中 d(i, j)d(i,j) 表示城市 ii 到城市 jj 之间灰尘度最小的路线对应的灰尘度的值。 为了改善出行环境, 每个城市都要有所作为, 当某个城市进行道路改善时, 会将与这个城市直接相连的所有道路的灰尘度都减少 1 , 但每条道路都有一个 灰尘度的下限值 LL, 当灰尘度达到道路的下限值时, 无论再怎么改善, 道路的 灰尘度也不会再减小了。

具体的计划是这样的:

第 1 天, 0 号城市对与其直接相连的道路环境进行改善;

第 2 天, 1 号城市对与其直接相连的道路环境进行改善;

$\cdots$
第 n天, n-1 号城市对与其直接相连的道路环境进行改善;

第 n+1 天, 0 号城市对与其直接相连的道路环境进行改善;

第 n+2天, 1 号城市对与其直接相连的道路环境进行改善;

LQ 国想要使得 PP 指标满足 $P\le Q$ 。请问最少要经过多少天之后, P 指标 可以满足 $P\le Q$。如果在初始时就已经满足条件, 则输出 0 ; 如果永远不可能 满足, 则输出 -1 。

解题思路

二分搜索+Floyd算法
对于P的定义已经给出很明显的提示了——多源最短路径，用Floyd，
灰尘度的变化是一个动态变化，而Floyd得到的最短路径抽象去了路径上的点，那样就不知道哪条最短路径会缩短了。
分析题意：
1）天数越多，就越可能达标
2）本题要求的是最少需要多少天
得出结论二分搜索

解题思路：二分搜索天数，用Floyd判断这天的灰尘度是否达标
注意点：
1、二分的上界

AC_Code

# -*- coding: utf-8 -*-
# @Author : BYW-yuwei
# @Software: python3.8.6
ans = float('inf')
edge = [0 for _ in range(105)]
min_edge = [0 for _ in range(105)]
dis = [[0 for _ in range(105)] for _ in range(105)]
down = [0 for _ in range(105)]
n,q = map(int,input().split())
for i in range(n):
    edge[i] = list(map(int,input().split()))
for i in range(n):
    min_edge[i] = list(map(int,input().split()))

def check(day):
    p=0
    op = day%n
    for i in range(n):
      if i<op:
        down[i] = day//n + 1
      else:
        down[i] = day//n
    for i in range(n):
        for j in range(n):
            dis[i][j] = max(edge[i][j] - down[i] - down[j],min_edge[i][j])
    for k in range(n):
        for i in range(n):
            for j in range(n):
                dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j])
    for i in range(n):
        for j in range(n):
            p += dis[i][j]
    if p <=q:
        return True
    else:
        return False
l=0
r=int(5e7)
while l<r:
    mid = (l+r)//2
    if check(mid):
        ans = min(ans,mid)
        r=mid
    else:
        l = mid +1
if l==int(5e7):
    print(-1)
else:
    print(ans)