一、题目

给你两个长度可能不等的整数数组 nums1 和 nums2 。两个数组中的所有值都在 1 到 6 之间（包含 1 和 6）。

每次操作中，你可以选择 任意 数组中的任意一个整数，将它变成 1 到 6 之间 任意 的值（包含 1 和 6）。

请你返回使 nums1 中所有数的和与 nums2 中所有数的和相等的最少操作次数。如果无法使两个数组的和相等，请返回 -1。

二、示例

2.1> 示例 1：

【输入】nums1 = [1,2,3,4,5,6], nums2 = [1,1,2,2,2,2]
【输出】3
【解释】你可以通过 3 次操作使 nums1 中所有数的和与 nums2 中所有数的和相等。以下数组下标都从 0 开始。

• 将 nums2[0] 变为 6 。 nums1 = [1,2,3,4,5,6], nums2 = [6,1,2,2,2,2] 。
• 将 nums1[5] 变为 1 。 nums1 = [1,2,3,4,5,1], nums2 = [6,1,2,2,2,2] 。
• 将 nums1[2] 变为 2 。 nums1 = [1,2,2,4,5,1], nums2 = [6,1,2,2,2,2] 。

2.2> 示例 2：

【输入】nums1 = [1,1,1,1,1,1,1], nums2 = [6]
【输出】-1
【解释】没有办法减少 nums1 的和或者增加 nums2 的和使二者相等。

2.3> 示例 3：

【输入】nums1 = [6,6], nums2 = [1]
【输出】3
【解释】你可以通过 3 次操作使 nums1 中所有数的和与 nums2 中所有数的和相等。以下数组下标都从 0 开始。

• 将 nums1[0] 变为 2 。 nums1 = [2,6], nums2 = [1] 。
• 将 nums1[1] 变为 2 。 nums1 = [2,2], nums2 = [1] 。
• 将 nums2[0] 变为 4 。 nums1 = [2,2], nums2 = [4] 。

提示：

• 1 <= nums1.length, nums2.length <= 10^5
• 1 <= nums1[i], nums2[i] <= 6

三、解题思路

首先，根据题意，我们需要计算出数组nums1和nums2之间，最小的操作次数，使得nums1的总和：sum(nums1)与nums2的总和：sum(nums2)两个值相等。那么我们可以根据如下4个步骤来解决这个问题：

【步骤1】分别计算sum(nums1)和sum(nums2)的值，确定两个数组加和的差值diff，以及sum(nums1)和sum(nums2)之间的大小关系。

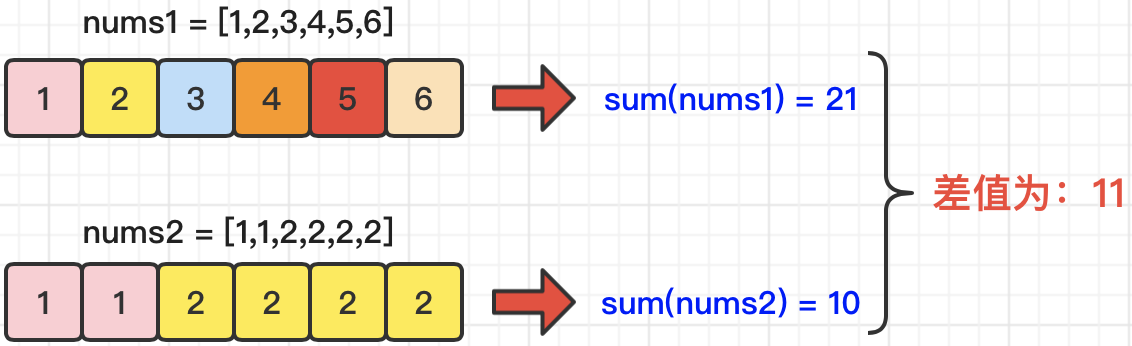
 【步骤2】将总和较小的数组赋值为int[] smaller，将总和较大的数组赋值为int[] bigger。

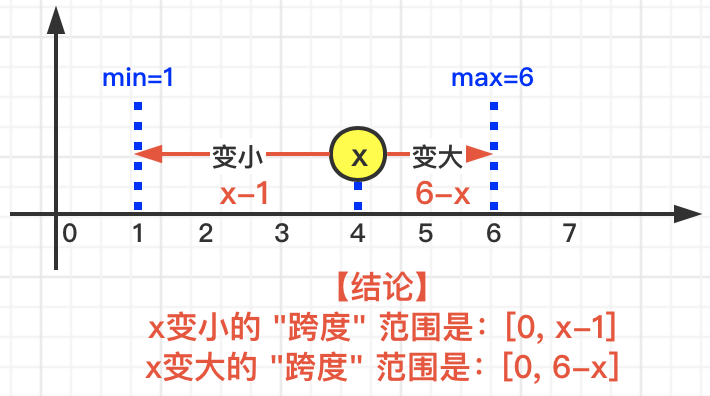
对于smaller数组中的每个值，我们要执行变大操作，其中：由于最大值是6，所以每个元素s变大的最大跨度是：6 - s；
对于bigger数组中的每个值，我们要执行变小操作，其中：由于最小值是1，所以每个元素b变大的最大跨度是：b - 1；

 【步骤3】创建一个用于存储跨度&出现次数的数组int[] range（也可以采用Map结构），其中：下标index表示跨度值，range[index]表示该跨度值出现的次数。由于题目中指出，nums1和nums2中元素的值的范围是[1, 6]，所以，对应的跨度值就是[0, 5]。为了便于画图，图中采用Map结构表示：

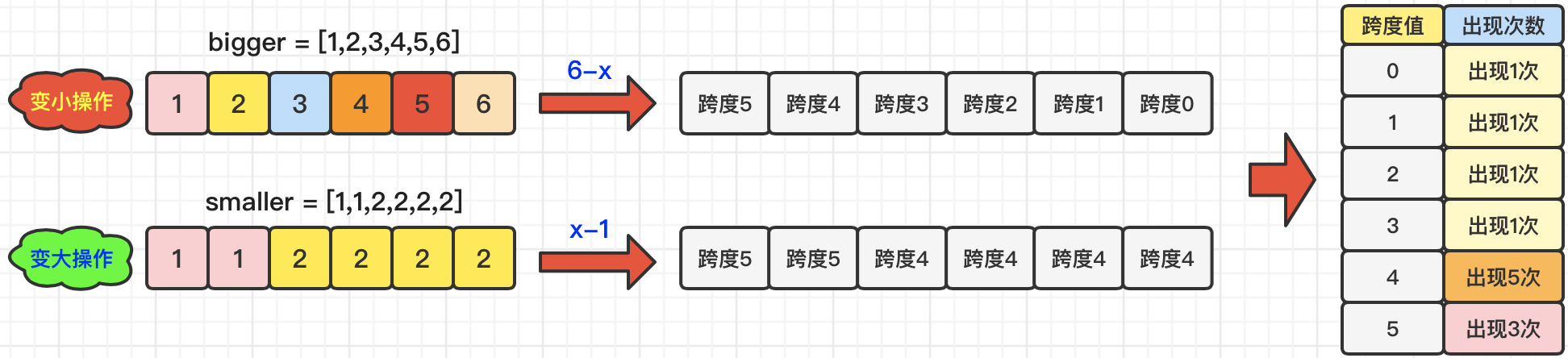
 【步骤4】由于要求计算出最小操作次数，所以我们需要从range数组末尾开始遍历执行对比操作，以上面图中的例子做演示，diff=11，range=[1,1,1,1,5,3]：

【第1次操作】因为差值diff > 跨度5，所以差值diff变为6（11减5），range[5]的出现次数变为2（3减1）；
【第2次操作】因为差值diff > 跨度5，所以差值diff变为1（6减5），range[5]的出现次数变为1（2减1）；
【第3次操作】因为差值diff <= 跨度5，满足题解，返回最少操作次数为：3。

四、代码实现

class Solution {
    public int minOperations(int[] nums1, int[] nums2) {
        int result = 0, l1 = nums1.length, l2 = nums2.length, sum1 = 0, sum2 = 0, diff;
        if (6 * l1 < l2 || 6 * l2 < l1) return -1; // 无法使两个数组的和相等，返回-1
        for (int n1 : nums1) sum1 += n1;
        for (int n2 : nums2) sum2 += n2;
        if ((diff = Math.abs(sum1 - sum2)) == 0) return 0; // 如果两个数组和相等，则不需要操作，返回0
        int[] range = calculate(nums1, nums2, sum1, sum2);
        for (int i = 5; i >= 0; i--) { // 从最大的差值开始对比
            while (range[i] > 0) { // 如果差值range[i]出现的次数不为0
                result++; // 操作次数加1
                if (i >= diff) return result; // 如果差值大于等于diff，则操作结束，返回操作数result
                range[i]--; // 差值range[i]的出现次数减1
                diff -= i; // 更新diff值
            }
        }
        return -1;
    }
    // 计算每个差值（1~5）出现的次数
    private int[] calculate(int[] nums1, int[] nums2, int sum1, int sum2) {
        int[] bigger = (sum1 < sum2) ? nums2 : nums1;
        int[] smaller = (sum1 < sum2) ? nums1 : nums2;
        int[] range = new int[6]; // index：差值  range[index]：该差值出现的次数
        for (int s : smaller) ++range[6 - s]; // 对于总数较小的数组，要执行增加操作，由于理论上最大值是6，所以最大可以增加"6-s"个数值
        for (int b : bigger) ++range[b - 1]; // 对于总数较大的数组，要执行减法操作，由于理论上最小值是1，所以最大可以减少"b-1"个数值
        return range;
    }
}

今天的文章内容就这些了：

写作不易，笔者几个小时甚至数天完成的一篇文章，只愿换来您几秒钟的 点赞 & 分享 。

更多技术干货，欢迎大家关注公众号“爪哇缪斯” ~ \(^o^)/ ~ 「干货分享，每天更新」