1. 引言
1)机器学习 > 表示学习 > 深度学习
表示学习是机器学习子集,其研究重点是如何⾃动找到合适的数据表示方式。深度学习是通过学习多层次的转换来进⾏的多层次的表示学习。
深度学习是机器学习的一个子集,但相比传统的机器学习方法,深度学习不仅取代了其浅层模型,⽽且取代了劳动密集型的特征⼯程。
2)数据、模型和算法
①与传统机器学习⽅法相⽐,深度学习的⼀个主要优势是可以处理不同⻓度的数据。②在没有⼤数据集的情况下,许多深度学习的效能并不⽐传统⽅法⾼。③数据的质量也很重要,如果数据中充满了错误,或者数据的特征不能预测任务⽬标,那么模型很可能⽆效。
3)实验环境
使用天池notebook(默认已安装pytorch),配置如下。
PS1="\[\e[33;1m\]\u\[\e[31;1m\]@\[\e[33;1m\]\h \[\e[36;1m\]\w\[\e[34;1m\]\n\$ \[\e[0m\]"
#pip install torch==1.12.0
#pip install torchvision==0.13.0
pip install d2l==0.17.6
mkdir d2l-zh && cd d2l-zh
curl https://zh-v2.d2l.ai/d2l-zh-2.0.0.zip -o d2l-zh.zip
unzip d2l-zh.zip && rm d2l-zh.zip
cd pytorch
2. 基础
2.1 张量
张量(tensor)表示一个由数值组成的数组,类似于numpy中的ndarray,但张量支持GPU加速运算和自动微分。
x = torch.arange(12)
#torch.zeros((2, 3, 4));torch.ones((2, 3, 4));torch.randn(3, 4) #全0;全1;标准正态分布
x.shape
X = x.reshape(3, 4)
2.2 张量运算
①按元素(elementwise)运算,如算数运算(+, -, *, /, **, …),逻辑运算(>, <, ==, …)等。
# 在相同形状的两个张量上执⾏按元素操作
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
X + Y; torch.exp(X); X.sum()
X == Y
#torch.cat((X, Y), dim=0); X.T #连接;转置
# 形状不同,通过⼴播机制执⾏按元素操作
a = torch.arange(3).reshape((3, 1)) #3 × 1
b = torch.arange(2).reshape((1, 2)) #1 × 2
a + b #广播为3 x 2,其中a复制列,b复制⾏,然后按元素相加
②线性代数运算,如向量点积,矩阵乘法等。
x = torch.tensor(3.0); y = torch.tensor(2.0) #实例化两个标量
x = torch.arange(4); y = torch.ones(4, dtype = torch.float32) #向量(一维张量)
torch.dot(x,y) #点积 -> 加权平均;夹角余弦
A = torch.arange(20).reshape(5, 4) #矩阵(二维张量)
A.sum(axis=[0, 1]) #对所有元素求和
A.sum(axis=1,keepdims=True) #非降维求和
A.mean() #求均值
B = A.clone()
A * B #Hadamard product, A⊙B
B = torch.ones(4, 3)
torch.mv(A, x) #matrix-vector product
torch.mm(A, B) #matrix-matrix multiplication(矩阵乘法)
1)线代
| 定义 | 数字表示法 | |
|---|---|---|
| 标量 | 仅包含⼀个数值被称为标量。 | 小写字母,如x,y,z; |
| 向量 | 标量值组成的列表。标量值被称为向量的元素或分量。 | 粗体、小写字母,如x,y,z;xi表示向量任一元素 |
| 矩阵 | 向量组成的列表。 | 粗体、⼤写字⺟,如X,Y,Z;xij表示第i行j列值 |
| 张量 | 具有任意数量轴的n维数组 | 特殊字体、大写字母,如X,Y,Z |
⽬标,或许是深度学习算法最重要的组成部分(除了数据),通常被表达为范数(L1, L2, Lp; Frobenius)。向量范数是将向量映射到标量的函数f。给定任意向量x,向量范数要满足以下属性:①如果按常数因⼦α缩放向量的所有元素,其范数也会按相同常数因子的绝对值缩放;②三⻆不等式;③⾮负;④范数最⼩为0,当且仅当向量全由0组成。
2)微积分

如果f′(a)存在,则称f在a处是可微(differentiable)的。如果f在⼀个区间内的每个数上都是可微的,则此函数在此区间中是可微的。
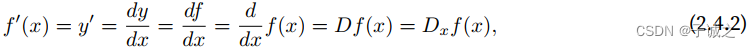
其中符号d/dx和D是微分运算符,表⽰微分操作。
常见函数的微分求解:…
常见函数的组合函数的微分求解:常数相乘法则;加法法则;乘法法则;除法法则;
多元函数的微分求解:偏导数(partial derivative);链式法则;
⾃动微分:深度学习框架⾃动计算导数。具体来说,系统会构建⼀个计算图,来跟踪计算是哪些数据通过哪些操作组合起来产⽣输出。⾃动微分使系统能够随后反向传播梯度。
# 例. 对函数y = 2x^{⊤}x关于列向量x求导
x = torch.arange(4.0)
x.requires_grad_(True)
y = 2 * torch.dot(x, x)
y.backward() #调⽤反向传播函数来⾃动计算y关于x每个分量的梯度
x.grad == 4 * x #快速验证这个梯度是否计算正确
# ⾮标量
x.grad.zero_() #在默认情况下, PyTorch会累积梯度,需要清除之前的值
y = x * x
y.backward(torch.ones(len(x))) #调⽤backward
x.grad
# 分离计算
x.grad.zero_()
y = x * x
u = y.detach()
z = u * x
z.sum().backward()
x.grad == u
3)概率
随机变量
概率
分布
…
2.3 数据预处理
import pandas as pd
import os
import torch
# 创建数据集
os.makedirs(os.path.join('..', 'data'), exist_ok=True)
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
f.write('NumRooms,Alley,Price\n') # 列名
f.write('NA,Pave,127500\n') # 每⾏表⽰⼀个数据样本
f.write('2,NA,106000\n')
f.write('4,NA,178100\n')
f.write('NA,NA,140000\n')
data = pd.read_csv(data_file)
inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2]
# 处理缺失值
inputs = inputs.fillna(inputs.mean()) # 连续值,插值法填充
inputs = pd.get_dummies(inputs, dummy_na=True) # 离散值,将NaN视为⼀个类别
# 转换为张量
X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)