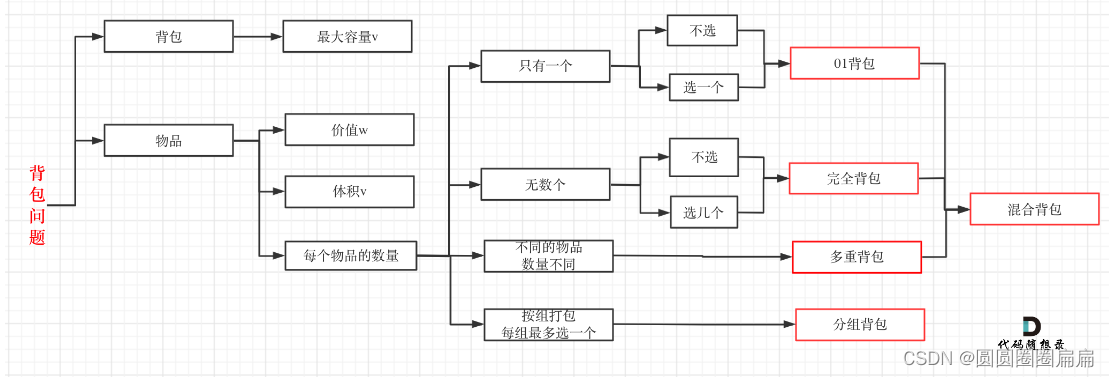
目录

01背包问题 二维

01背包问题 一维

416. 分割等和子集

---

背包问题分为：01背包，完全背包，多种背包

01背包问题 二维

动态规划五部曲：

• 初始化

首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。如图：

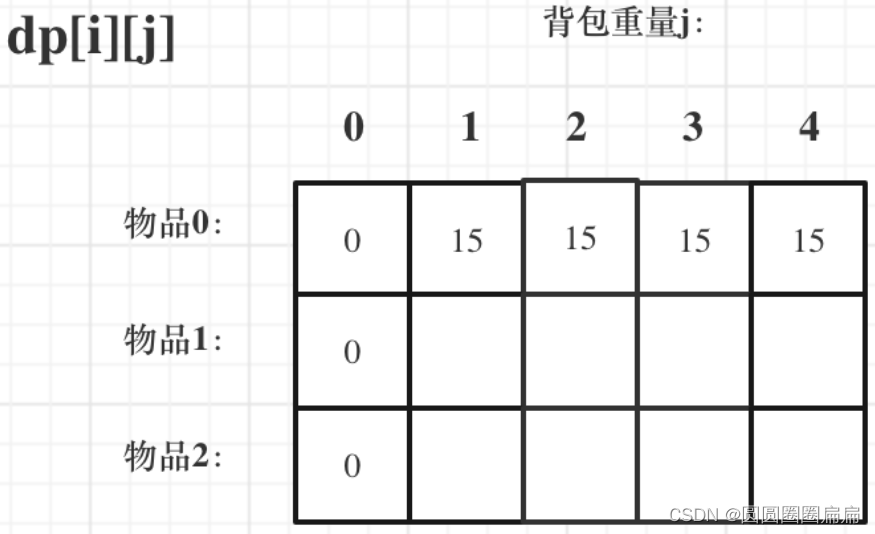
 最后

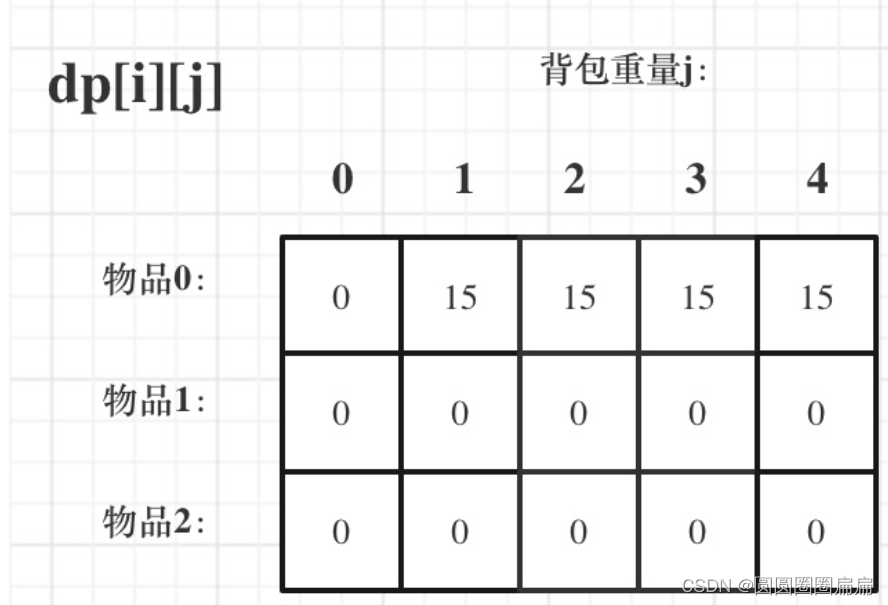
• 遍历顺序

遍历顺序可以先遍历物品，也可以先遍历书包重量

• dp数组的定义以及含义

即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

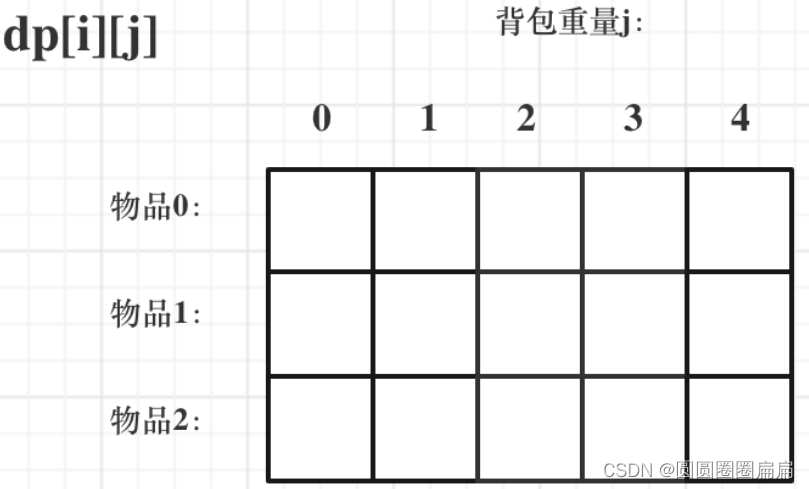
• 递归公式

dp[i][j]分为两种情况，一种是取i这个物品，一种是不取i这个物品

取i这个物品:

dp[i-1][j-weight[i]]+value[i]

由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值

不取i这个物品：dp[i-1][j]

由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以被背包内的价值依然和前面相同。)

然后两个取其中的最大值

• 打印dp数组

代码随想录

视频讲解：带你学透0-1背包问题！| 关于背包问题，你不清楚的地方，这里都讲了！| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili

01背包问题 一维

滚动数组的想法，不断的取更新数组

代码随想录

视频讲解：带你学透01背包问题（滚动数组篇） | 从此对背包问题不再迷茫！_哔哩哔哩_bilibili

面试问题：

二维数组实现后，遍历顺序可以调换吗？

一维数组实现后，遍历顺序可以调换吗？for循环为什么是从后往前，而不是从前往后

416. 分割等和子集

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        target = sum(nums)
        #如果nums中的数无法平均拆成两半，那么返回false
        if target % 2 == 1: return False
        target //= 2
        #定义dp数组，并且确定其含义，dp[j]意味着取j容量的最大价值，这里价值和容量相等
        dp = [0] *10001
        #遍历物体
        for i in range(len(nums)):
        #遍历容量，容量要从后向前遍历才不会取重复物体
            for j in range(target, nums[i] - 1, -1):
                #分两种情况，取i/不取i，不取i的话，就是dp[j]。
                #取i物品的话，dp[j-nums[i]] j容量需要减去物品i的容量，再加上它的价值
                dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])
        #最后背包容量是target，dp[target]是装满背包后的容量
        if target == dp[target]:
            return True
        else:
            return False

时间超时了，我也不知道为什么

本题是 01背包的应用类题目

代码随想录

视频讲解：动态规划之背包问题，这个包能装满吗？| LeetCode：416.分割等和子集_哔哩哔哩_bilibili