简介
最近在学习传感器相关的知识,在国外的一篇论文学习过程中,觉得这篇论文的校准方法是个不错的参考。
这种校准简单且比较鲁棒的算法,操作简单,且除了偏移与比例系数,还可以估计出传感器 xyz 轴相对于标准正交三轴的偏移(因为传感器的物理 xyz 轴可能不是标准正交的),不过相比六面校准,其算法的计算过程要复杂许多。
其校准过程也并不复杂:
1)初始静止一段时间
2)旋转 IMU 到另一个角度之后静止
3)等待一段采样时间
4)继续旋转,重复 2)3)步骤,达到预定的采样次数
5)估计参数
思路
理想的 IMU,x,y,z 三轴是独立正交的,理想的三轴坐标系,加速度计的理想坐标系可以记作 AOF,实际中的 IMU 的坐标轴并不是标准正交的,其与标准正交坐标系有一定的偏移,将各轴的偏移记作 β,之后建立误差模型,建立代价函数,进而求解估计参数。
加速度计部分
坐标轴定义
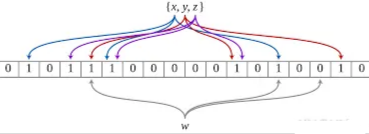
假设现有一个标准正交坐标系,记作 s(B),当前坐标轴记作 s(S) ,当前轴可能是非正交的,从 y 轴到 z 轴的偏移记作 β(yz),其他的以此类推,那么 从 s(S) 转换到正交坐标系 s(B) 的表达式就可以写作如下形式:

T 是其中的旋转矩阵,为:

以此为基础,将加速度计的标准正交轴记作 a(B),加速度计当前坐标轴记作 a(S) ,但上面的旋转矩阵 T 有点复杂,需要对其进行简化,现给出两个坐标轴选取时的条件:
1)定义加速度计的标准正交轴为 AOF,加速度计实际的坐标轴记作 AF(AF不一定正交),将 AOF 的 x 轴与 AF 的 x 轴重合
2)AOF 的 y 轴定义在 AF 的x 与 y 轴组成的平面上
按照上述的两个原则建立坐标轴,那么在上述旋转矩阵的 β(xz),β(xy) 就消除为 0,因为AOF 与 AF 的 x 轴已经重合了,因此 x 轴相对 y,z 轴的偏移就消除掉了。
同事,因为 AOF 的 y 轴在 AF 的 x,y 轴组成的平面上,因此 y 相对于 x 的偏移也消除掉了,即 β(yx) = 0。
那么针对加速度计,上述坐标轴的表达式就可以写作:
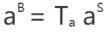

加速度计模型
在加速度计的零偏与比例系数的基础上,加上上述的坐标轴偏移,就可以得到加速度计的模型。
加速度计的比例系数矩阵记作 K(a):

加速度计的零偏向量记作 b(a):

加速度计整体的误差模型就可以写作:

v 表示测量噪声,a(O) 表示标准轴的加速度值,a(S) 表示真实轴上的加速度计测量值。
此方程中,含有 9 个未知量,三轴的轴偏移,三轴的比例系数,三轴的零偏。将代估变量记作 θ:

将测量噪声忽略掉,误差模型就可以写作:

代价函数建立
对于此方程,不用六面校准,而是任意角度的加速度计数据的话,采样一定量的数据之后,可以利用这个原理来列出其代价函数:
静止状态下,加速度计三轴的数据的平方和等于重力加速度 g
其代价函数就可以写作:

以上的代价函数是有加法的,运用最小二乘法来估计参数比较困难,因此使用 LM 算法来进行非线性估计,具体 LM 算法的原理与实现,参考主页中的上一篇文章《LM迭代估计法》
陀螺仪部分
陀螺仪的校准需要依赖于加速度计的校准。总体思路为:
1.在进行完上一步的加速度计估计参数的计算之后,利用加速度计已经校准过的参数矩阵对之前采样的数据进行校正
2.在采样时的每一次静止时的加速度计数据进行校正后,可以得到一个较为准确的重力加速度向量值
3.当前静止时的重力加速度向量记作初始重力加速度向量,然后在旋转IMU时,使用陀螺仪的数据对重力向量进行积分,可以得到一个旋转后(到下一次静止采集数据)的重力向量预测值
4.再次使用加速度计的数据得到一个重力加速度向量值
5.利用加速度计得到的重力加速度向量与陀螺仪积分得到的重力加速度向量做差,平方的方式,建立代价函数
6.求解代价函数,得到陀螺仪的估计参数
误差模型建立
陀螺仪与加速度计的坐标轴应该选择相同的参考坐标轴,也就是 AOF ,但对于陀螺仪来说,因为选取的加速度计的标准正交轴,一些坐标轴的偏移量就不能消除了,还是需要加上,即:


其中,T 为旋转矩阵,W(O) 表示陀螺仪的正交标准轴,与 AOF 重合,W(S) 是当前的陀螺仪轴
比例系数与偏移系数矩阵都与加速度计的形式是相同的:


误差模型的形式也是相同的:

在后续的计算中,测量误差 v 可以忽略。
代价函数建立
按照上述的步骤说明,代价函数使用加速度计校准后得到的准确的重力加速度向量与陀螺仪积分得到的重力加速度向量的各项差的平方和来建立:

同样,使用 LM 算法来进行参数的估计