计算物理专题：双向打靶法解决本征值问题

双向打靶法全部代码

EigenMethods.py

import numpy as np
import matplotlib.pyplot as plt
from SchrodingerTools import *

#type-ode1:
## y''(x)+f(x)y(x) = g(x)
##tips:
##lambda eigen,x:f(eigen,x)

def replace_eigen(eigen):
    def decorator(func):
        def wrapper(x):
            return func(eigen, x)
        return wrapper
    return decorator

def bisection(X,Y):
    assert len(X)==len(Y),"X is not as long as Y"
    Num = len(X)
    Zeropoints = []
    for i in range(Num-1):
        if Y[i]*Y[i+1]<=0:
            Zeropoints.append((X[i]+X[i+1])/2)
    return Zeropoints
    
class ode1():
    def __init__(self,f,g,x0,x1,y0=0,y1=0,dy0=1,dy1=1,ddy0=0,ddy1=0,h=0.01,EigenRange=[-2,2],EigenStep=0.001):
        self.f = f
        self.g = g
        self.x0 = x0
        self.x1 = x1
        self.y0 = y0
        self.y1 = y1
        self.dy0 = dy0
        self.dy1 = dy1
        self.ddy0 = ddy0
        self.ddy1 = ddy1
        self.h = h
        self.EigenRange = EigenRange
        self.EigenStep = EigenStep
        
    def Shooting(self):
        ChoosePoint=(self.x0+self.x1)/2
        PossibleEigen = np.arange(self.EigenRange[0],self.EigenRange[1],self.EigenStep)
        Distance = []
        
        for EigenValue in PossibleEigen:
            @replace_eigen(EigenValue)
            def new_f(EigenValue,x):
                return self.f(EigenValue,x)

            @replace_eigen(EigenValue)
            def new_g(EigenValue,x):
                return self.g(EigenValue, x)
            
            forward_Y = numerov_forward(new_f,new_g,self.x0,self.x1,self.y0,self.dy0,self.ddy0,self.h)
            backward_Y = numerov_backward(new_f,new_g,self.x0,self.x1,self.y1,self.dy1,self.ddy1,self.h)

            forward_derivative = First_order_derivative(forward_Y,ChoosePoint)
            backward_derivative = First_order_derivative(backward_Y,ChoosePoint)

            Distance.append((forward_Y[round(ChoosePoint/self.h)]/forward_derivative)-(backward_Y[round(ChoosePoint/self.h)]/backward_derivative))
    
        ##plt.plot(PossibleEigen,Distance)
        ##plt.pause(0.01)
        ##plt.title("Distance -- Possible Eigenvalue")

        #print(bisection(PossibleEigen,Distance))

        ZeroPoints = bisection(PossibleEigen,Distance)
        Deviations = []
        for EigenValue in ZeroPoints:
            @replace_eigen(EigenValue)
            def new_f(EigenValue,x):
                return self.f(EigenValue,x)

            @replace_eigen(EigenValue)
            def new_g(EigenValue,x):
                return self.g(EigenValue, x)

            forward_Y = numerov_forward(new_f,new_g,self.x0,self.x1,self.y0,self.dy0,self.ddy0,self.h)
            backward_Y = numerov_backward(new_f,new_g,self.x0,self.x1,self.y1,self.dy1,self.ddy1,self.h)

            plt.figure()
            plt.plot(np.arange(self.x0,self.x1+self.h,self.h),forward_Y,label="forward_Y")
            plt.plot(np.arange(self.x0,self.x1+self.h,self.h),backward_Y,label="backward_Y")
            plt.title("$"+str(round(EigenValue,4))+"$")
            plt.xlabel("$deviation"+str(round(abs(forward_Y[-1]-self.y1)+abs(backward_Y[0]-self.y0),4))+"$")
            plt.pause(0.01)
            
        return [PossibleEigen,Distance,ZeroPoints]

ScrodingTools.py

import numpy as np
import matplotlib.pyplot as plt


#一阶导公式：序列，位置，步长，阶数
def First_order_derivative(Y,x,h=0.01,order=4):
    n = round(x/h)
    if order==4:
        try:
            return (Y[n-2]-8*Y[n-1]+8*Y[n+1]-Y[n+2])/(12*h)
        except:
            print("First_order_derivative:Failure!")
            
    elif order==2:
        try:
            return (Y[n+1]-Y[n-1])/(2*h)
        except:
            print("First_order_derivative:Failure!")
            

#二阶导公式：序列，位置，步长，阶数
def Second_order_derivative(Y,x,h=0.01,order=4):
    n = round(x/h)
    if order==4:
        try:
            return -(Y[n-2]-16*Y[n-1]+30*Y[n]-16*Y[n+1]+Y[n+2])/(12*h**2)
        except:
            print("Second_order_derivative:Failure!")
            
    elif order==2:
        try:
            return (Y[n-1]-2*Y[n]+Y[n+1])/(h**2)
        except:
            print("Second_order_derivative:Failure!")


#numerov 向前方法
#f函数,g函数,起始点x0，终止点x1，起始点函数值y0，起始点导数值dy0，
#起始点二阶导数值ddy0(0)，间隔(0.01)
            
def numerov_forward(f,g,x0,x1,y0=0,dy0=1,ddy0=0,h=0.01):
    
    X = np.arange(x0,x1+h,h)
    try:
        F = f(X)    
    except:
        print("numerov_forward:Function F failure")
        F[0]=0
        F[1:] = f(X[1:])

    try:
        G = g(X)    
    except:
        print("numerov_forward:Function G failure")
        G[0]=0
        G[1:] = g(X[1:])        
        
    Num = len(X)
    Y = np.zeros(Num)
    Y[0] = y0
    Y[1] = y0 + h*dy0 + 1/2 * h**2 * ddy0

    try:
        for i in range(2,Num):
            k1 = 2*(1-5*h**2/12*F[i-1])*Y[i-1]
            k2 = h**2*G[i-1]-(1+h**2/12*F[i-2])*Y[i-2]
            Y[i] = (k1+k2)/(1+h**2/12*F[i])
        return Y
    except Exception as e:
        print("numerov_forward:Failure!  ",e)  


#numerov 向后方法
#f函数,g函数,起始点x0，终止点x1，终止点函数值y1，终止点导数值dy1，
#起始点二阶导数值ddy1(0)，间隔(0.01)
def numerov_backward(f,g,x0,x1,y1=0,dy1=1,ddy1=0,h=0.01):

    X = np.arange(x0,x1+h,h)
    try:
        F = f(X)    
    except:
        print("numerov_forward:Function F failure")
        F[0]=0
        F[1:] = f(X[1:])

    try:
        G = g(X)    
    except:
        print("numerov_forward:Function G failure")
        G[0]=0
        G[1:] = g(X[1:])        
        
    Num = len(X)
    Y = np.zeros(Num)
    Y[-1] = y1
    Y[-2] = y1 - h*dy1 - 1/2 * h**2 * ddy1

    try:
        for i in range(Num-3,-1,-1):
            k1 = 2*(1-5*h**2/12*F[i+1])*Y[i+1]
            k2 = h**2*G[i+1]-(1+h**2/12*F[i+2])*Y[i+2]
            Y[i] = (k1+k2)/(1+h**2/12*F[i])
        return Y
    except Exception as e:
        print("numerov_backward:Failure!  ",e)  
    
#雅克比方法求特征值
def sign(x):
    if x>0:
        return 1.0
    elif x<0:
        return -1.0
    elif x==0:
        return 0.0

def jacobi_eigenvalue(A, tol=1e-10,max_iter=500):
    n = A.shape[0]
    V = np.eye(n) 
    iterations = 0

    while True:
        max_idx = np.argmax(np.abs(np.triu(A, k=1)))
        i, j = divmod(max_idx, n)
        if np.abs(A[i,j]) < tol or iterations >= max_iter:
            print("end!!")
            break
        Lambda = abs(A[j,j]-A[i,i])
        Mu = 2.0 * A[i,j] * sign(A[j,j]-A[i,i])
        if Lambda**2+Mu**2 != 0:
            Omega = Lambda/(Lambda**2+Mu**2)**0.5
            c = ((1+Omega)/2)**0.5       
            s = Mu*Omega/(Lambda*(2*(1+Omega))**0.5)
        else:
            c = 2**0.5/2
            s = 2**0.5/2
        J = np.eye(n)
        J[i, i] = c
        J[j, j] = c
        J[i, j] = s
        J[j, i] = -s
        A = np.dot(np.dot(J.T, A), J)
        V = np.dot(V, J)
        iterations += 1
    eigenvalues = np.diag(A)
    eigenvectors = V.T
    return eigenvalues, eigenvectors

test.py

import numpy as np
import matplotlib.pyplot as plt
from SchrodingerTools import *
from EigenMethods import *

def f(EigenValue,x):
    return x**2-EigenValue*x*40
def g(EigenValue,x):
    return EigenValue + x**5

x0 = 0
x1 = 1

y0 = 0
y1 = 0

dy0 = 1
dy1 = 1

O = ode1(f,g,x0,x1)
a = O.Shooting()

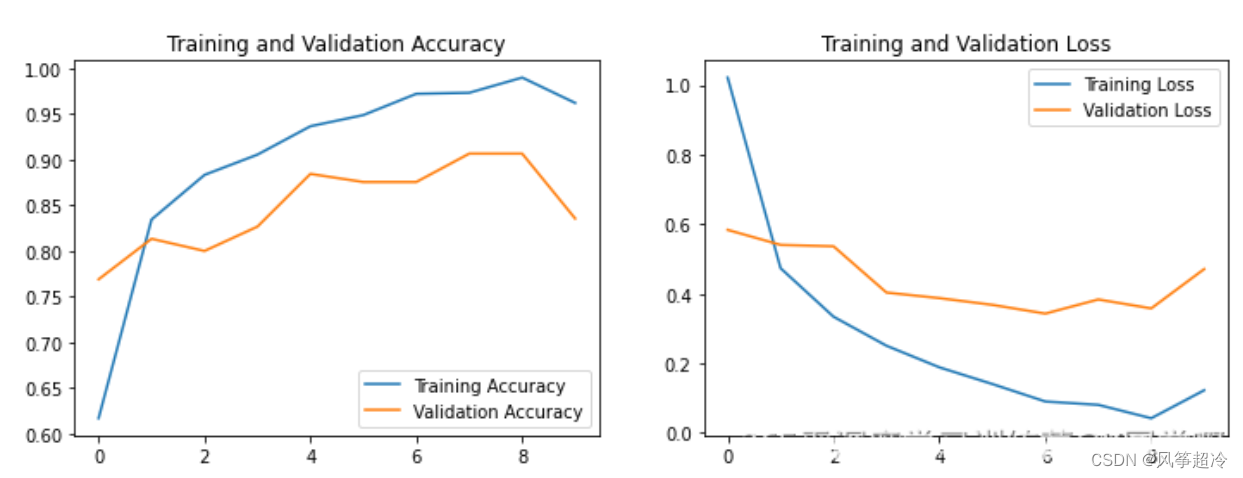
运行结果

扫描隧道显微镜调研

\subsection{扫描隧道显微镜单原子操纵技术}
   1990年，美国IBM公司的两位科学家发现，靠近探针的氙原子随探针作同样的移动。纳米科学技术正是依赖于STM这种能够操纵原子的工具而诞生和发展的。\par
\subsubsection{扫描隧道显微镜单原子操纵的方式}
   单原子操纵分横向操纵和纵向操纵两种。横向操纵指被操纵的原子在操纵过程中始终在表面上移动, 没有脱离表面的束缚, 即原子和表面之间的键不曾断裂。纵向操纵是指利用探针把单个原子从表面提起使之吸附到探针上而脱离表面束缚, 或再把原子从探针重新释放到表面,操纵过程中原子和表面之间的键会发生断裂。\par

   横向操纵通常采用恒定电流模式，探针的高度不断变化。首先，经过对隧道电流的调整，STM探针将被调整到一个合适的高度以增强它对吸附原子的作用力。其次，STM将维持在恒定电流工作模式，将被吸附的原子移动到目标位置。最后，STM探针将升起以断开与原子间的联系，原子将被固定到目标位置上。\par

   纵向操纵通过调整探针和材料表面之间的电场，以完成原子的吸附，移动和固定。纵向操纵单原子的放置分成三种方式。其一，被放置的原子来源于STM的针尖。其二，被放置的原子来源于样本。其三，被放置的原子由某种方式运输到STM针尖上，然后再被放置到样品表面。\par

\subsubsection{扫描隧道显微镜单原子操纵的原理}
   电场蒸发法：在STM针尖和样品表面之间施加一数伏数十毫秒宽的电压脉冲。针尖和样品表面之间的距离约为$0. 3～1. 0nm$，针尖和样品之间的电场数量级在$10^9～10^{10}V/m$之间。样品上的原子在强电场的作用下被吸附到探针上，实现单原子的移动和提取操纵。\par

   调控原子间作用力：探针尖端和试样原子间力主要是范德华力、静电力。当探针接近试样时，原子间的作用力使得探针可能吸附或释放单个原子。1993年，Eigler等将吸附在Cu表面上48个Fe原子逐个移动并排列成一圆形量子栅栏，制成了那张著名的照片。



   人工化学反应操控：首先，在针尖和式样之间填充反应性气体，利用STM的隧道能量，促使目标原子和样品表面原子发生化学反应吸附在一起以实现对局部原子的操纵。\par

\section{扫描隧道显微镜技术的发展方向}
\subsection{单原子开关}
   1990年,Eigler研究小组使用STM成功地移动了吸附在Ni原子表面上的氙原子。当改变STM针尖和镍表面之间的偏压和极性时,氙原子总是偏向正极一端。当氙原子与STM探针接触时，STM与Ni金属表面形成的STM隧道处于高导电状态。当Xe原子回到Ni金属表面上后，STM隧道回到低导电状态，从而构建起了一个超高速双稳态电子开关。
\subsection{单原子存储器}
   单原子存储器可能依赖STM以两种方式实现。其一可能是利用表层单原子的空穴作为一个比特存储信息：通过移走表面上的几个原子来写入信息；通过填补表面的缺陷来删除已写入的信息或者清楚不平整的表面产生的“噪声”。其二是讲放置到表面上的单原子作为存储信息的一个比特，步骤与上类似。单原子存储器的容量会更大，一块面积为1$cm^2$的Si可以存储$10^{15}$比特的信息

\subsection{超快扫描隧道显微镜技术$^{[3]}$}
   多数的扫描隧道显微镜只能在较低的磁场下观测准静态过程，不能满足对实时的，动态的变化过程观测的需要。光耦合扫描隧道显微镜技术将扫描隧道显微镜(Scanning Tunneling Microscope，STM)和光激发技术相结合，能够在原子级的空间分辨下探测对光激发敏感的动力学过程。\par
   光学手段和STM耦合的方式包括：\par
   1．光源激发样品时，STM停止工作并后撤针尖。在照射激光前后使用STM进行原位扫描，表征光激发对样品表面产生的影响。该方式不涉及激光和隧穿电流的直接耦合。\par
   2．激光和STM隧道电子的直接耦合测量。\par
   3．使用针尖诱导的隧道节发光或分子发光，用光谱仪收集或成像。\par
   4．STM和光学pump—probe技术的联合，同时实现原子级空间分辨和fs超快时间分辨。\par