本篇文章为LeetCode 字符串匹配模块的刷题笔记,仅供参考。
目录
- Leetcode28.找出字符串中第一个匹配项的下标
- Leetcode214.最短回文串
- Leetcode459.重复的子字符串
- Leetcode686.重复叠加字符串匹配
- Leetcode1023.驼峰式匹配
- Leetcode1392.最长快乐前缀
- Leetcode1668.最大重复子字符串
Leetcode28.找出字符串中第一个匹配项的下标
Leetcode28.找出字符串中第一个匹配项的下标
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 1:
输入:haystack = “sadbutsad”, needle = “sad”
输出:0
解释:“sad” 在下标 0 和 6 处匹配。第一个匹配项的下标是 0,所以返回 0。
示例 2:
输入:haystack = “leetcode”, needle = “leeto”
输出:-1
解释:“leeto” 没有在 “leetcode” 中出现,所以返回 -1 。
提示:
1 <= haystack.length, needle.length <= 104
haystack 和 needle 仅由小写英文字符组成
法一:由于本题中主串和模式串都比较短,因此可以直接双层 for 循环暴力搜索,时间复杂度是 O(m*n):
class Solution {
public:
int strStr(string haystack, string needle) {
int m=haystack.size();
int n=needle.size();
for(int i=0;i<=m-n;i++){
bool flag=true;
for(int j=0;j<n;j++){
if(haystack[i+j]!=needle[j]){
flag=false;
break;
}
}
if(flag) return i;
else continue;
}
return -1;
}
};

法二:其实本题是 KMP 算法 的经典例题,在主串和子串更长时仍能获得较好的效果,参考【宫水三叶】简单题学 KMP 算法。先构造模式串(即子串)p 的部分匹配值表 next,next[i] 表示模式串的子串 p[0…i] 的 最长前后缀匹配长度,即满足 p[0...k] == p[i-k...i] 条件的最大 k+1 值(0<=k<i);然后再遍历主串进行匹配。
先采用双指针思想构造模式串 p 的 next 数组:i 表示当前待计算模式串的结束位置(即 p[0…i] 为 next 欲构造的当前字符串),也就是后缀的最后一位;j 表示前一种情况中和后缀匹配的最长前缀的后一位(即 p[0…j-1] 和后缀 p[i-j…i-1] 已经匹配)。使用双指针 i 和 j 构造 next 数组的流程如下:
- 若
p[i] == p[j]:则前缀 p[0…j] 和后缀 p[i-j…i] 匹配(因为 p[0…j-1] 和 p[i-j…i-1] 已经匹配),于是next[i] = j+1,然后 i 和 j 同时后移一位; - 若
p[i] != p[j]:则说明 p[0…j] 和 p[i-j…i] 无法匹配,需要指针 j 回退,直到p[i] == p[j]或者j == 0。如果是p[i] == p[j],则进入前一种情况;如果是j == 0时还是有p[i] != p[j],则前后缀完全不匹配,因此next[i] = 0,i 后移一位,j 保持 0(j=0 表示完全不匹配)。然而,这里的回退并不是j--,因为 p[j’] == p[i] 并不保证 p[0…j’] 和 p[i-j’…i] 能够匹配(j’ < j)。思索一下可以发现,p[0…j’] 和 p[i-j’…i] 能够匹配的充要条件是p[j'] == p[i]且p[0...j'-1] == p[i-j'...i-1]。前一个条件已经作为循环终止的条件,后一个可以作为选取 j’ 的标准。又由于p[0...j-1] == p[i-j...i-1](巧妙利用已经求解过的 next[0…i-1]),因此p[0...j'-1] == p[i-j'...i-1]等价于p[0...j'-1] == p[j-j'...j-1],即选取 j’ 的标准是p[0...j'-1] == p[j-j'...j-1],即next[j-1] = j':
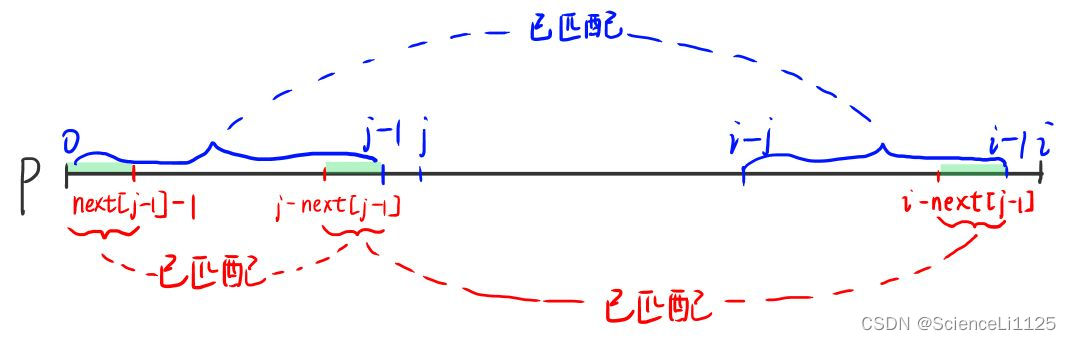
构造 next 数组的时间复杂度是 O(n),可以参见下面的写法:

考虑 2i-j 的值,每次循环这个值都至少会加 1,而它又是小于 2n 的,因此构造 next 数组的时间复杂度是 O(n)。
构造完 next 数组后就可以在 O(m) 的时间内遍历主串进行匹配。还是采用双指针,i 表示主串的当前位置,j 表示模式串的当前位置(p[0…j-1] 和 s[i-j…i-1] 已经匹配),都从 0 开始计数:
- 若
p[i] == s[j]:则 p[0…j] 和 s[i-j…i] 也匹配,i 和 j 同时后移一位; - 若
p[i] != s[j]:原本需要 j 归零并且 i 后移一位后再重新匹配,但根据 next 数组,next[j-1] 表示 p[0…next[j-1]-1] 和 p[j-next[j-1]…j-1] 匹配,又有 p[0…j-1] 和 s[i-j…i-1] 已经匹配,所以 s[i-next[j-1]…i-1] 可以和 p[0…next[j-1]-1] 匹配。于是 j 不必归零,而是从next[j-1]处开始匹配即可:
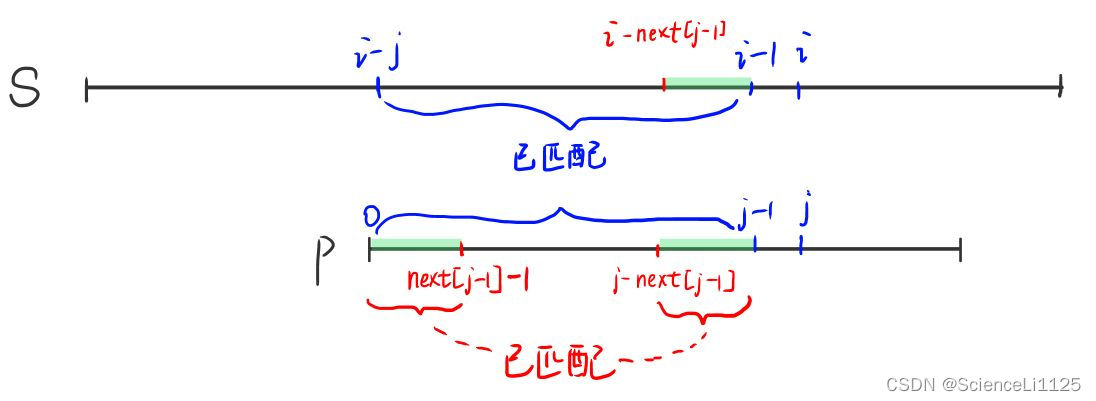
class Solution {
public:
void getNext(string p,vector<int> &v){
v[0]=0;
int j=0; // 刚开始还没开始匹配
for(int i=1;i<p.size();i++){
if(p[i]==p[j]){
v[i]=j+1;
j++;
}else{
while(j>0){
if(p[i]==p[j]){
v[i]=j+1;
j++;
break;
}else{
j=v[j-1];
}
}
if(j==0){
if(p[i]!=p[j]){
v[i]=0;
}
else{
v[i]=1;
j=1;
}
}
}
}
}
int strStr(string haystack, string needle) {
int m=haystack.size();
int n=needle.size();
vector<int> next(n);
getNext(needle,next);
int j=0;
for(int i=0;i<m;i++){
if(haystack[i]==needle[j]){
j++;
}else{
while(j>0){
if(haystack[i]==needle[j]){
j++;
break;
}else{
j=next[j-1];
}
}
if(j==0 && haystack[i]==needle[j]) j++;
}
if(j==n) return i-n+1;
}
return -1;
}
};

上面的写法有些复杂,可以参考下面整合过的:
class Solution {
public:
void getNext(string p,vector<int> &v){
v[0]=0;
int j=0; // 刚开始还没开始匹配
for(int i=1;i<p.size();i++){
while(j>0 && p[i]!=p[j]){
j=v[j-1];
}
if(p[i]==p[j]){
j++;
}
v[i]=j;
}
}
int strStr(string haystack, string needle) {
int m=haystack.size();
int n=needle.size();
vector<int> next(n);
getNext(needle,next);
int j=0;
for(int i=0;i<m;i++){
while(j>0 && haystack[i]!=needle[j]){
j=next[j-1];
}
if(haystack[i]==needle[j]){
j++;
}
if(j==n) return i-n+1;
}
return -1;
}
};
Leetcode214.最短回文串
Leetcode214.最短回文串
给定一个字符串 s,你可以通过在字符串前面添加字符将其转换为回文串。找到并返回可以用这种方式转换的最短回文串。
示例 1:
输入:s = “aacecaaa”
输出:“aaacecaaa”
示例 2:
输入:s = “abcd”
输出:“dcbabcd”
提示:
0 <= s.length <= 5 * 104
s 仅由小写英文字母组成
法一:暴力枚举,设 s 的逆序串为 s’,最短回文串的实质就是在 s 中找到最大的 i,使得 s’[0…n-i] + s[0…n-1] 是回文串。
class Solution {
public:
string shortestPalindrome(string s) {
int n=s.size();
if(n==0) return s;
bool flag=true;
for(int i=0;i<s.size()/2;i++){
if(s[i]!=s[n-1-i]){
flag=false;
break;
}
}
if(flag) return s;
string subs="";
for(int i=0;i<n;i++){
subs.push_back(s[n-1-i]);
string stmp=subs+s;
int m=stmp.size();
flag=true;
for(int j=0;j<stmp.size()/2;j++){
if(stmp[j]!=stmp[m-1-j]){
flag=false;
break;
}
}
if(flag) return stmp;
}
return "";
}
};
时间复杂度 O(n2),遗憾超时…
法二:设 s’ 表示 s 的逆序串。将 s 分为两个部分:最长回文串 s1 和后缀 s2,本题就是要得到最长 s1。由于 s1 是回文串,因此 s1=s1’,又有 s1 是 s 的前缀,s1’ 是 s’ 的后缀,所以 s1 是 s’ 的后缀。
仍然使用 KMP 算法,但由于 s1 不确定长度,因此需要对 KMP 终止条件进行调整。先计算模式串 s 的 next 数组,然后在 s’ 中匹配 s。因为 s 和 s’ 长度相同,因此除非 s 本身就是回文串,不然永远无法匹配成功。因此不需要在 s’ 中成功匹配 s,而是在 s’ 达到末尾时,当前匹配成功的 s 的子串就是 s1:
class Solution {
public:
void getNext(string s,vector<int> &v){
v[0]=0;
int j=0;
for(int i=1;i<s.size();i++){
while(j>0 && s[i]!=s[j]){
j=v[j-1];
}
if(s[i]==s[j]){
j++;
}
v[i]=j;
}
}
string shortestPalindrome(string s) {
int n=s.size();
if(n==0) return s;
string rs(s.rbegin(),s.rend());
vector<int> next(n);
getNext(s,next);
int j=0;
for(int i=0;i<n;i++){
while(j>0 && rs[i]!=s[j]){
j=next[j-1];
}
if(rs[i]==s[j]){
j++;
}
}
return rs.substr(0,n-j)+s;
}
};

Leetcode459.重复的子字符串
Leetcode459.重复的子字符串
给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。
示例 1:
输入: s = “abab”
输出: true
解释: 可由子串 “ab” 重复两次构成。
示例 2:
输入: s = “aba”
输出: false
示例 3:
输入: s = “abcabcabcabc”
输出: true
解释: 可由子串 “abc” 重复四次构成。 (或子串 “abcabc” 重复两次构成。)
提示:
1 <= s.length <= 104
s 由小写英文字母组成
字符串匹配问题如果想使用 KMP 算法,就需要构造子串(模式串)和主串,但本题只有一个字符串 s。如果将两个 s 拼接就可以形成主串,记为 S,则 s 也可以当做模式串。如果 s 能够匹配 S 并且第一次匹配的位置落在区间 (0, n) 内,貌似就可以满足题目的要求,下面证明:

图中的蓝线标记了 s 在 S 中的匹配位置,红线标记了 S[0…n-1] 是由 s 而来的。设匹配位置为 i,因为 S[0...n-1] == s[0...n-1] == S[i...n+i-1],所以 S[0...i-1] == S[i...2i-1];又通过 S[i...2i-1] == s[i...2i-1] 和 S[2i...3i-1] == s[i...2i-1],可得 S[i...2i-1] == S[2i...3i-1]。以此类推,可以不断推出 S[(k-1)i...ki-1] == S[ki...(k+1)i-1] 直到 s 的末尾(但不一定正好紧贴 n-1,假设结束位置是 tk-1 <= n-1),即字符串 S 的前缀是通过它的一个子串重复多次构成,现在只需要证明该子串可以构造到 S 的尾部即可,即 2n % i == 0。因为 S[n...n+i-1] == s[n-i...n-1],所以 s 的最后 i 位也是由该子串构成的,可以通过反证法证明 2n % i == 0。
为了 s 不匹配到位置 0,在构造 S 的时候令 S = s.substr(1,n-1)+s;为了 s 不匹配到位置 n 及其后,在匹配时计算匹配位置并判断是否超过 n-1:
class Solution {
public:
void getNext(string p, vector<int> &v){
v[0]=0;
int j=0;
for(int i=1;i<p.size();i++){
while(j>0 && p[i]!=p[j]){
j=v[j-1];
}
if(p[i]==p[j]){
j++;
}
v[i]=j;
}
}
bool repeatedSubstringPattern(string s) {
int n=s.size();
if(n<=1) return false;
string S=s.substr(1,n-1)+s;
vector<int> next(n);
getNext(s,next);
int j=0;
for(int i=0;i<2*n-1;i++){
while(j>0 && s[j]!=S[i]){
j=next[j-1];
}
if(s[j]==S[i]) j++;
if(j==n) return true;
if(i-j+1>=n-1) return false; // 防止匹配位置超过n
}
return false;
}
};

Leetcode686.重复叠加字符串匹配
Leetcode686.重复叠加字符串匹配
给定两个字符串 a 和 b,寻找重复叠加字符串 a 的最小次数,使得字符串 b 成为叠加后的字符串 a 的子串,如果不存在则返回 -1。
注意:字符串 “abc” 重复叠加 0 次是 “”,重复叠加 1 次是 “abc”,重复叠加 2 次是 “abcabc”。
示例 1:
输入:a = “abcd”, b = “cdabcdab”
输出:3
解释:a 重复叠加三遍后为 “abcdabcdabcd”, 此时 b 是其子串。
示例 2:
输入:a = “a”, b = “aa”
输出:2
示例 3:
输入:a = “a”, b = “a”
输出:1
示例 4:
输入:a = “abc”, b = “wxyz”
输出:-1
提示:
1 <= a.length <= 104
1 <= b.length <= 104
a 和 b 由小写英文字母组成
显然,需要先重复叠加几次 a 直到长度超过 b 后再进行 KMP 匹配。需要先计算叠加的次数:
- 如果 a 比 b 长,那么最多只需要叠加 2 次即可,因为 b 可能匹配到 { a[i…n-1], a[0…j] };
- 如果 a 比 b 短,就需要多次叠加,上取整计算
n = a.length() / b.length(),最多只需要叠加 n+1 次;
综上,n = nb/na + (nb%na!=0) + 1。随后在叠加后的 a 中匹配 b 即可:
class Solution {
public:
void getNext(string p,vector<int> &v){
v[0]=0;
int j=0;
for(int i=1;i<p.size();i++){
while(j>0 && p[i]!=p[j]) j=v[j-1];
if(p[i]==p[j]) j++;
v[i]=j;
}
}
int repeatedStringMatch(string a, string b) {
int na=a.size();
int nb=b.size();
int n=nb/na+(nb%na!=0)+1;
string s="";
for(int i=0;i<n;i++) s+=a;
vector<int> next(nb);
getNext(b,next);
int j=0;
int index=-1;
for(int i=0;i<s.size();i++){
while(j>0 && s[i]!=b[j]) j=next[j-1];
if(s[i]==b[j]) j++;
if(j==nb){
index=i-j+1; // 因为i还没+1,所以此时的i表示的是当前已经匹配过的位置
break;
}
}
if(index<0) return -1;
if(na>=nb){ // 最多只需要重复叠加2次
if((index+nb)>na) return 2;
else return 1;
}else{
return (index+nb)/na+((index+nb)%na!=0);
}
}
};

Leetcode1023.驼峰式匹配
Leetcode1023.驼峰式匹配
给你一个字符串数组 queries,和一个表示模式的字符串 pattern,请你返回一个布尔数组 answer 。只有在待查项 queries[i] 与模式串 pattern 匹配时, answer[i] 才为 true,否则为 false。
如果可以将小写字母插入模式串 pattern 得到待查询项 query,那么待查询项与给定模式串匹配。可以在任何位置插入每个字符,也可以不插入字符。
示例 1:
输入:queries = [“FooBar”,“FooBarTest”,“FootBall”,“FrameBuffer”,“ForceFeedBack”], pattern = “FB”
输出:[true,false,true,true,false]
示例:
“FooBar” 可以这样生成:“F” + “oo” + “B” + “ar”。
“FootBall” 可以这样生成:“F” + “oot” + “B” + “all”.
“FrameBuffer” 可以这样生成:“F” + “rame” + “B” + “uffer”.
示例 2:
输入:queries = [“FooBar”,“FooBarTest”,“FootBall”,“FrameBuffer”,“ForceFeedBack”], pattern = “FoBa”
输出:[true,false,true,false,false]
解释:
“FooBar” 可以这样生成:“Fo” + “o” + “Ba” + “r”.
“FootBall” 可以这样生成:“Fo” + “ot” + “Ba” + “ll”.
示例 3:
输入:queries = [“FooBar”,“FooBarTest”,“FootBall”,“FrameBuffer”,“ForceFeedBack”], pattern = “FoBaT”
输出:[false,true,false,false,false]
解释:
“FooBarTest” 可以这样生成:“Fo” + “o” + “Ba” + “r” + “T” + “est”.
提示:
1 <= pattern.length, queries.length <= 100
1 <= queries[i].length <= 100
queries[i] 和 pattern 由英文字母组成
采用双指针匹配即可,不需要 KMP 算法:
class Solution {
public:
bool Match(string query, string pattern){
int i=0,j=0;
for(j=0;j<pattern.size();j++){
while(i<query.size() && query[i]!=pattern[j] && query[i]>='a' && query[i]<='z'){
i++;
}
if(query[i]==pattern[j]) i++;
else return false;
}
for(int k=i+1;k<query.size();k++){
if(query[k]>='A' && query[k]<='Z') return false;
}
return true;
}
vector<bool> camelMatch(vector<string>& queries, string pattern) {
int n=queries.size();
vector<bool> ans(n);
for(int i=0;i<n;i++){
ans[i]=Match(queries[i],pattern);
}
return ans;
}
};

Leetcode1392.最长快乐前缀
Leetcode1392.最长快乐前缀
「快乐前缀」 是在原字符串中既是 非空 前缀也是后缀(不包括原字符串自身)的字符串。
给你一个字符串 s,请你返回它的 最长快乐前缀。如果不存在满足题意的前缀,则返回一个空字符串 “” 。
示例 1:
输入:s = “level”
输出:“l”
解释:不包括 s 自己,一共有 4 个前缀(“l”, “le”, “lev”, “leve”)和 4 个后缀(“l”, “el”, “vel”, “evel”)。最长的既是前缀也是后缀的字符串是 “l”。
示例 2:
输入:s = “ababab”
输出:“abab”
解释:“abab” 是最长的既是前缀也是后缀的字符串。题目允许前后缀在原字符串中重叠。
提示:
1 <= s.length <= 105
s 只含有小写英文字母
仔细阅读不难发现,本题其实是模式串的 next 数组的来源:模式串 p 的部分匹配值数组 next,next[i] 表示模式串的子串 p[0…i] 的 最长前后缀匹配长度,即满足 p[0...k] == p[i-k...i] 条件的最大 k+1 值(0<=k<i);
class Solution {
public:
void getNext(string p,vector<int> &v){
v[0]=0;
int j=0;
for(int i=1;i<p.size();i++){
while(j>0 && p[i]!=p[j]){
j=v[j-1];
}
if(p[i]==p[j]) j++;
v[i]=j;
}
}
string longestPrefix(string s) {
int n=s.size();
vector<int> next(n);
getNext(s,next);
return s.substr(0,next[n-1]);
}
};

Leetcode1668.最大重复子字符串
Leetcode1668.最大重复子字符串
给你一个字符串 sequence ,如果字符串 word 连续重复 k 次形成的字符串是 sequence 的一个子字符串,那么单词 word 的 重复值为 k 。单词 word 的 最大重复值 是单词 word 在 sequence 中最大的重复值。如果 word 不是 sequence 的子串,那么重复值 k 为 0 。
给你一个字符串 sequence 和 word ,请你返回 最大重复值 k 。
示例 1:
输入:sequence = “ababc”, word = “ab”
输出:2
解释:“abab” 是 “ababc” 的子字符串。
示例 2:
输入:sequence = “ababc”, word = “ba”
输出:1
解释:“ba” 是 “ababc” 的子字符串,但 “baba” 不是 “ababc” 的子字符串。
示例 3:
输入:sequence = “ababc”, word = “ac”
输出:0
解释:“ac” 不是 “ababc” 的子字符串。
提示:
1 <= sequence.length <= 100
1 <= word.length <= 100
sequence 和 word 都只包含小写英文字母。
遍历字符串 sequence,在 sequence[i…n-1] 中匹配字符串 word 并记录最大的重复值。在遍历过程中,如果当前匹配位置与上一次相邻,即 it-1 + word.size() == it,那么重复值就可以 +1;否则重复值需要清零。为了记录相邻两次匹配坐标,可以使用双指针进行记录。
但当匹配值不连续时,并不能直接继续匹配,因为在 it-1 和 it 之间还可能有其他匹配值。如 sequence = “aaabaaaabaaabaaaabaaaabaaaabaaaaba”,word = “aaaba” 的情况,第三次匹配到的下标为 14,并且与上一次不连续,如果直接清零从 14 开始匹配的话就会忽略了 9 处的匹配字符串,影响结果:
class Solution {
public:
void getNext(string p,vector<int> &v){
v[0]=0;
int j=0;
for(int i=1;i<p.size();i++){
while(j>0 && p[i]!=p[j]){
j=v[j-1];
}
if(p[i]==p[j]){
j++;
}
v[i]=j;
}
}
int strStr(string haystack, string needle) {
int m=haystack.size();
int n=needle.size();
vector<int> next(n);
getNext(needle,next);
int j=0;
for(int i=0;i<m;i++){
while(j>0 && haystack[i]!=needle[j]){
j=next[j-1];
}
if(haystack[i]==needle[j]){
j++;
}
if(j==n) return i-n+1;
}
return -1;
}
int maxRepeating(string sequence, string word) {
int maxrep=0;
int i=strStr(sequence.substr(0),word); // i为起始位置
int pre_i=-1; // 前一次i的匹配值
int cur_len=0;
while(i<sequence.size()){
if(i==-1){
break;
}else if((pre_i+word.size())==i){
cur_len+=1;
maxrep=max(maxrep,cur_len);
pre_i=i;
int tmp=strStr(sequence.substr(i+word.size()),word);
if(tmp==-1) break;
i+=(word.size()+tmp);
}else{
i=pre_i+1; // 不连续时i需要回退
int tmp=strStr(sequence.substr(i),word);
if(tmp==-1) break;
i+=tmp;
pre_i=i-word.size();
cur_len=0;
}
}
return maxrep;
}
};