【LeetCode热题100】打卡第27天：二叉树的前序、中序、后序遍历

⛅前言

大家好，我是知识汲取者，欢迎来到我的LeetCode热题100刷题专栏！

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。在此专栏中，我们将会涵盖各种类型的算法题目，包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等，并会提供详细的解题思路以及Java代码实现。如果你也想刷题，不断提升自己，就请加入我们吧！QQ群号：827302436。我们共同监督打卡，一起学习，一起进步。

LeetCode热题100专栏🚀：LeetCode热题100

Gitee地址📁：知识汲取者 (aghp) - Gitee.com

题目来源📢：LeetCode 热题 100 - 学习计划 - 力扣（LeetCode）全球极客挚爱的技术成长平台

PS：作者水平有限，如有错误或描述不当的地方，恳请及时告诉作者，作者将不胜感激

📕二叉树的前序遍历

中左右

🔒题目

原题链接：144.二叉树的前序遍历

🔑题解

解法一：递归实现

在使用DFS时，也经常这么用O(∩_∩)O

public class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        traversalTree(ans, root);
        return ans;
    }

    private void traversalTree(List<Integer> ans, TreeNode root) {
        if (root==null){
            return;
        }
        ans.add(root.val);
        traversalTree(ans, root.left);
        traversalTree(ans, root.right);
    }
}

复杂度分析：

时间复杂度： $O (n)$
空间复杂度： $O (n)$

其中 $n$ 为数组中元素的个数

解法二：迭代实现

这个理解起来也不难，本质上和解法一是一样的。就是使用栈模拟递归的过程，区别是递归过程中是隐士的维护一个栈，而这里是显示维护一个栈。不是很理解的话，可以画个草图

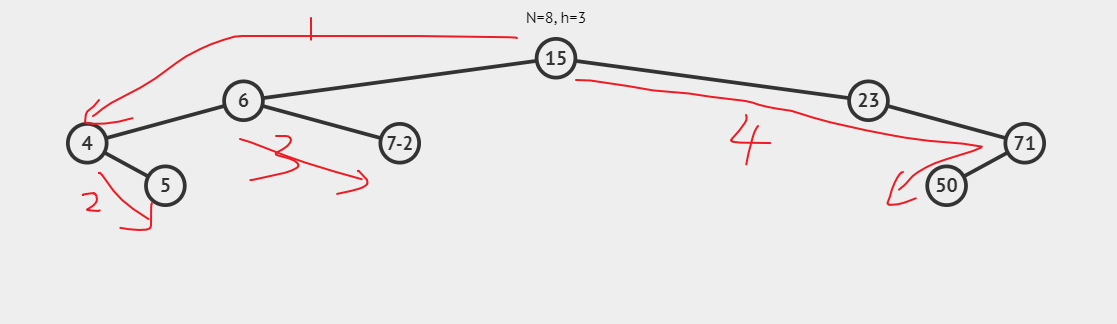
public class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        Deque<TreeNode> stack = new ArrayDeque<>();
        TreeNode cur = root;
        while (!stack.isEmpty() || cur != null){
            // 第一遍循环，把根节点左子树所有根节点入栈
            // 后面再入栈右节点
            while (cur != null){
                ans.add(cur.val);
                stack.push(cur);
                cur = cur.left;
            }
            // 自底向上出栈
            TreeNode node = stack.pop();
            if (node.right != null){
                cur = node.right;
            }
        }
        return ans;
    }
}

复杂度分析：

时间复杂度： $O (n)$
空间复杂度： $O (n)$

其中 $n$ 为数组中元素的个数

📕二叉树的中序遍历

左中右

🔒题目

原题链接：94.二叉树的中序遍历

🔑题解

解法一：递归实现

public class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        traversal(ans, root);
        return ans;
    }

    private void traversal(List<Integer> ans, TreeNode root) {
        if (root == null){
            return;
        }
        traversal(ans, root.left);
        ans.add(root.val);
        traversal(ans, root.right);
    }
}

解法二：迭代实现

public class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        Deque<TreeNode> stack = new ArrayDeque<>();
        TreeNode cur = root;
        while (!stack.isEmpty() || cur != null) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode node = stack.pop();
            ans.add(node.val);
            if (node != null){
                cur = node.right;
            }
        }
        return ans;
    }
}

📕二叉树的后序遍历

左右中

🔒题目

原题链接：145.二叉树的后序遍历

🔑题解

解法一：递归实现

public class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        traversal(ans, root);
        return ans;
    }

    private void traversal(List<Integer> ans, TreeNode root) {
        if (root == null){
            return;
        }
        traversal(ans, root.left);
        traversal(ans, root.right);
        ans.add(root.val);
    }
}

解法二：迭代实现

感觉这个是三个当中最难的想了好久😫，难点在于要防止死循环

PS：有可能是今天题目写的有点多了，头有点晕了🤣

public class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        Deque<TreeNode> stack = new ArrayDeque<>();
        TreeNode cur = root;
        TreeNode pre = null;
        while (!stack.isEmpty() || cur != null) {
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            // 自底向上出栈
            cur = stack.pop();
            if (cur.right == null || cur.right == pre) {
                // 右节点为空 或 右节点已遍历
                ans.add(cur.val);
                pre = cur;
                cur = null;
            }else {
                // 左子树遍历完，右节点不为空，右节点要先输出
                // 将当前根节点加入，因为当前根节点要在右节点之后输出
                stack.push(cur);
                // 将当前指针改成右节点，用于遍历右子树
                cur = cur.right;
            }
        }
        return ans;
    }
}

二叉树遍历——迭代统一写法

参考：「代码随想录」帮你对二叉树不再迷茫，彻底吃透前中后序递归法（递归三部曲）和迭代法（不统一写法与统一写法） - 二叉树的后序遍历 - 力扣（LeetCode）

注意：统一写法的栈不能使用ArrayDeque，因为ArrayDeque的add方法如果添加null元素会直接爆NPE

这种统一写法的好处，再与你只要是熟悉一种写法，其它写法信手拈来，但是效率没有前面的高（经过提交测试），但有一说一我还是喜欢前面的写法，不太喜欢这种统一的写法

/**
 * @author ghp
 * @title 前序遍历
 */
class Solution {

    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        if (root != null) stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node != null) {
                if (node.right != null) stack.push(node.right);
                if (node.left != null) stack.push(node.left);
                stack.push(node);
                stack.push(null);

            } else {
                node = stack.peek();
                stack.pop();
                ans.add(node.val);
            }
        }
        return ans;
    }
}

class Solution {

    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        if (root != null) stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node != null) {
                if (node.right != null) stack.push(node.right);
                stack.push(node);
                stack.push(null);
                if (node.left != null) stack.push(node.left);
            } else {
                node = stack.peek();
                stack.pop();
                ans.add(node.val);
            }
        }
        return ans;
    }
}

class Solution {

    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        if (root != null) stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node != null) {
                stack.push(node);
                stack.push(null);
                if (node.right != null) stack.push(node.right);
                if (node.left != null) stack.push(node.left);
            } else {
                node = stack.peek();
                stack.pop();
                ans.add(node.val);
            }
        }
        return ans;
    }
}