系列文章目录

第一章 AlexNet网络详解

第二章 VGG网络详解

第三章 GoogLeNet网络详解 

第四章 ResNet网络详解 

第五章 ResNeXt网络详解 

第六章 MobileNetv1网络详解 

第七章 MobileNetv2网络详解 

第八章 MobileNetv3网络详解 

第九章 ShuffleNetv1网络详解 

第十章 ShuffleNetv2网络详解 

第十一章 EfficientNetv1网络详解 

第十二章 EfficientNetv2网络详解 

第十三章 Transformer注意力机制

第十四章 Vision Transformer网络详解 

第十五章 Swin-Transformer网络详解 

第十六章 ConvNeXt网络详解 

第十七章 RepVGG网络详解 

第十八章 MobileViT网络详解 

文章目录

•  EfficientNetv1网络详解
• 0. 摘要
• 1. 前言
• 2.   EfficientNetv1网络详解网络架构
  • 1.  EfficientNetv1_Model.py(pytorch实现）
  • 2.
• 总结

---

0、摘要

1. 根据以往的经验，增加网络的深度depth能够得到更加丰富、复杂的特征并且能够很好的应用到其他任务中。但是网络的深度过深会面临梯度消失，训练困难问题。
2. 增加网络的width能够获得更高细粒度的特征并且也更容易训练，但对于width很大而且深度较浅的网络往往很难学习到更深层次的特征。
3. 增加输入网络的图像分辨率能够潜在获得更高细粒度的特征模板，但对于非常高的输入分辨率，准确率的增益也会减少。并且大分辨率图像会增加计算量。

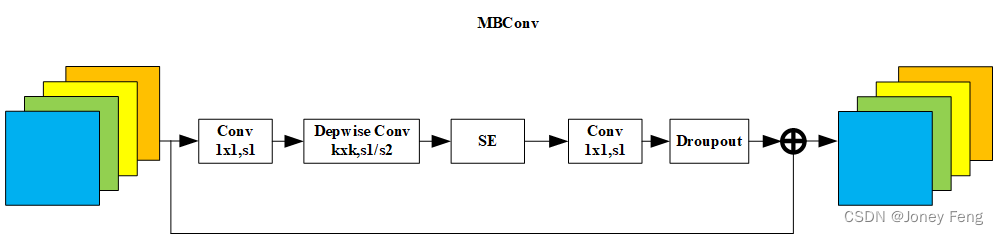
1. 第一个升维的1x1卷积层，它的卷积核个数是输出特征矩阵channel的n倍
2. 当n=1时，不要第一个升维的1x1卷积层，即Stage2中的MBConv结构都没有第一个升维的1x1卷积层(这和MobileNetV3网络类似)
3. 关于shortcut连接，仅当输入MBConv结构的特征矩阵与输出的特征矩阵shape相同时才存在。

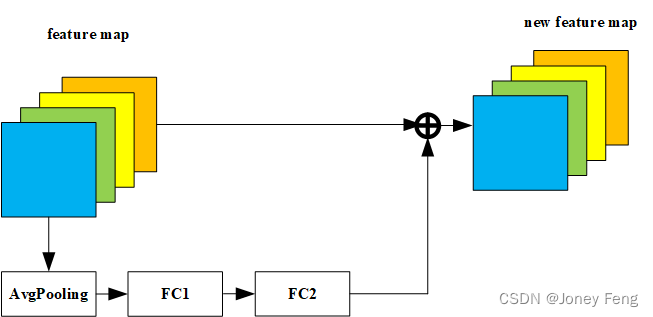
SE模块如图所示，由一个全局平均池化，两个全连接层组成。第一个全连接层的节点个数是输入该MBConv特征矩阵channels的1/4，且使用Swish激活函数。第二个全连接层的节点个数等于Depthwise Conv层输出的特征矩阵channels，且使用Sigmoid函数

---------------------------------------------------------------------------------------------------------------------------------

Width_coefficient代表channel维度上的倍率因子，比如在EfficientNetB0中Stage1的3x3卷积层所使用的卷积核个数是32，那么在B6中就是32x1.8=57.6接着取整到离它最近的8的倍数即56，其他Stage同理

Depth_coefficient代表depth维度上的倍率因子（仅针对Stage2到Stage8），比如EfficientNetB0中Stage7的L4,那么在B6中就是4x2.6=10.4，接着向上取整即11.

---------------------------------------------------------------------------------------------------------------------------------

卷积神经网络(ConvNets)通常在固定的资源预算下开发，如果有更多的资源可用，再进行扩展以获得更好的准确性。在本文中，我们系统地研究了模型扩展，并确定了仔细平衡网络深度、宽度和分辨率可以带来更好的性能。基于这一观察结果，我们提出了一种新的缩放方法，使用一个简单但高效的复合系数均匀缩放深度/宽度/分辨率的所有维度。我们展示了这种方法在扩展MobileNets和ResNet方面的有效性。为了更进一步，我们使用神经架构搜索设计了一个新的基线网络，并将其扩展为一系列模型，称为EfficientNets，这些模型比以前的ConvNets具有更好的准确性和效率。特别是，我们的EfficientNet-B7在ImageNet上实现了最先进的84.3% top-1准确率，而在推断时比最好的现有ConvNet小8.4倍，快6.1倍。我们的EfficientNets也具有良好的转移性，在CIFAR-100 (91.7%)、Flowers (98.8%)和其他3个转移学习数据集上实现了最先进的准确性，并且参数数量更少一个数量级。

1、前言

通过扩展 ConvNets 的规模，通常可以实现更高的准确度。例如，ResNet (He et al.，2016)可以通过添加更多层次来从 ResNet-18 扩展到 ResNet-200；最近，GPipe (Huang et al.，2018)通过将基线模型扩大四倍来实现 84.3％ 的 ImageNet top-1 准确度。然而，扩展 ConvNets 的过程从未被很好地理解，目前有许多可行的方式。最常见的方式是通过网络深度 (He et al.，2016) 或宽度 (Zagoruyko和Komodakis，2016) 扩展 ConvNets。另一种不太常见但日益流行的方法是通过图像分辨率 (Huang et al.，2018) 扩展模型。在以前的工作中，通常只扩展三种尺寸中的一种 - 深度、宽度和图像大小。虽然可以任意扩展两个或三个尺寸，但任意扩展需要繁琐的手动调整，而且通常仍会导致次优的准确度和效率。在本文中，我们想研究和重新思考扩展 ConvNets 的过程。特别是，我们研究了一个核心问题：是否存在一种基本方法来扩展 ConvNets，以实现更好的准确度和效率？我们的实证研究表明，平衡网络宽度/深度/分辨率的所有维度至关重要，令人惊讶的是，可以通过简单地将它们各自扩大一定比例来实现这种平衡。基于这一观察结果，我们提出了一种简单而有效的复合缩放方法。与任意缩放这些因素的传统做法不同，我们的方法统一缩放网络宽度、深度和分辨率，将它们与常数比例相结合。并采用一组固定的缩放系数进行分辨率调整。例如，如果我们想要使用2N倍的计算资源，那么我们可以简单地通过将网络深度增加αN倍、宽度增加βN倍、图像大小增加γN倍来实现，其中α，β，γ是由原始小模型进行小格子搜索确定的常数系数。图2说明了我们的缩放方法与传统方法之间的差异。从直觉上讲，复合缩放方法是有意义的，因为如果输入图像更大，则网络需要更多的层数来增加感受野，并需要更多的通道来捕捉更细粒度的图案。事实上，以前的理论(Raghu等人，2017; Lu等人，2018)和经验结果(Zagoruyko & Komodakis，2016)都表明网络宽度和深度之间存在某种关系，但据我们所知，我们是第一个在所有三个维度(网络宽度、深度和分辨率)之间经验性地量化这种关系。我们展示了我们的缩放方法在现有的MobileNets (Howard等人，2017; Sandler等人，2018)和ResNet (He等人，2016)上的良好效果。值得注意的是，模型缩放的有效性严重依赖于基础网络。为了更进一步，我们使用神经体系结构搜索(Zoph & Le，2017; Tan等人，2019)来开发一个新的基础网络，并将其扩展以获得一组模型，称为EfficientNets。图1总结了ImageNet的表现，其中我们的EfficientNets明显优于其他ConvNets。特别地，我们的EfficientNet-B7超过了现有的最佳GPipe准确性(Huang等人，2018)，但使用的参数数量少8.4倍，推理速度快6.1倍。与广泛使用的ResNet-50(He等人，2016)相比，我们的EfficientNet-B4将top-1准确度从76.3%提高到83.0%(+6.7%)，具有类似的FLOPS。除了ImageNet之外，EfficientNets也很好地转化，并在8个广泛使用的数据集中的5个上实现了最新的准确性，在减少达到21倍的参数的同时，就已经超过了现有的ConvNets。

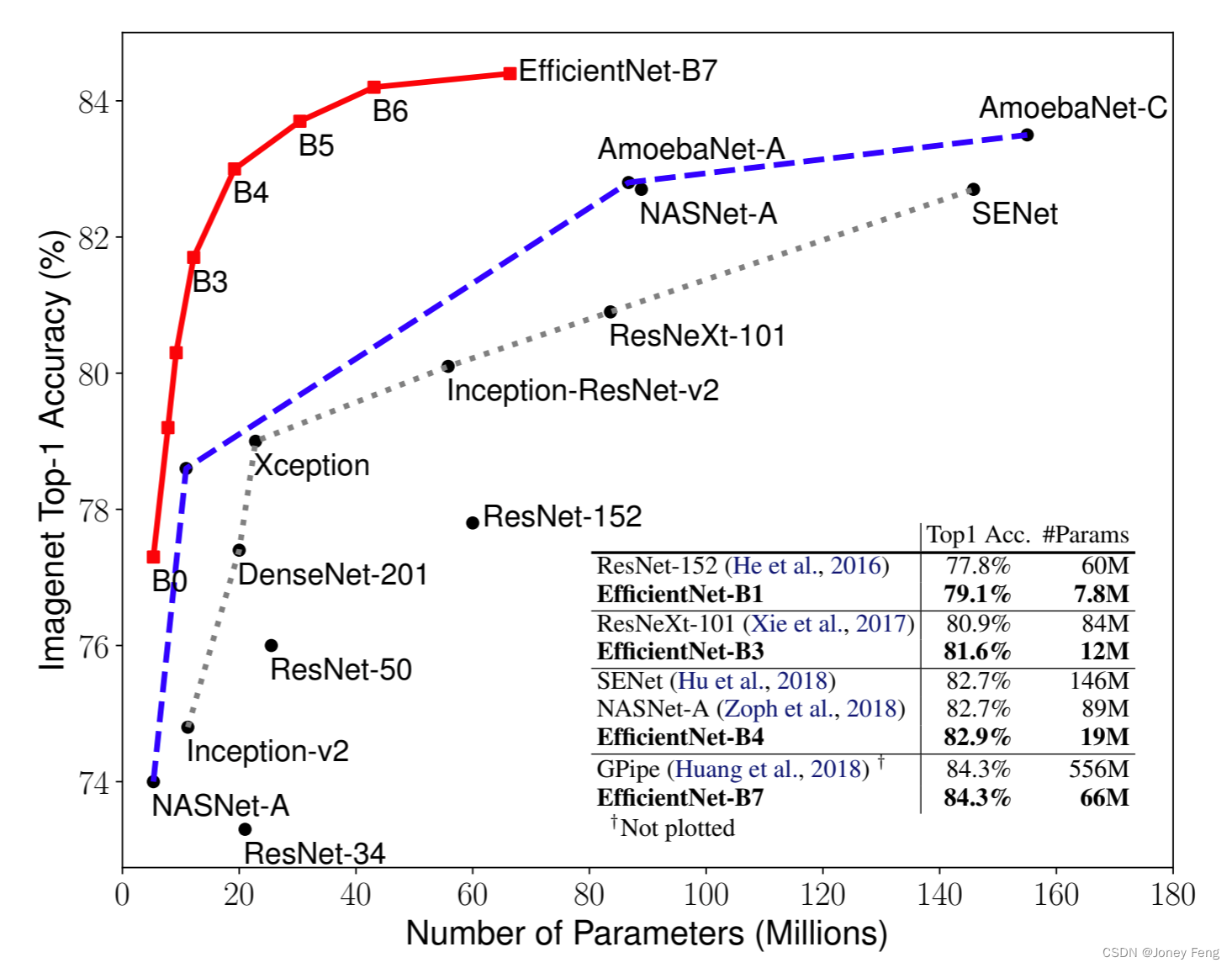
 （图1.模型大小与ImageNet准确性。所有数字都是基于单张图片、单个模型的结果。我们的EfficientNets明显优于其他ConvNets。特别是，EfficientNet-B7在比GPipe小8.4倍、速度快6.1倍的情况下实现了新的84.3％top-1准确率的最佳表现。EfficientNet-B1比ResNet-152小7.6倍、速度快5.7倍。详情请参见表二和表四。）

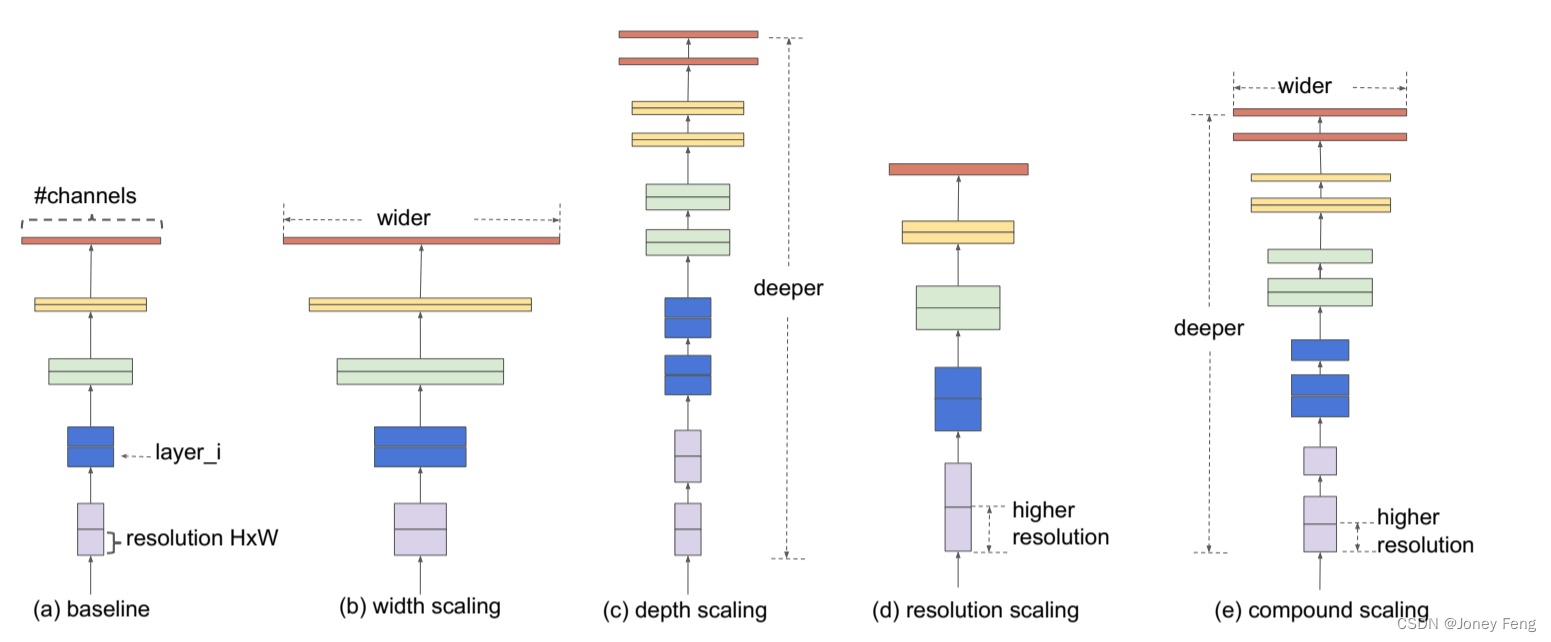
 （图2.模型缩放。(a)是基准网络示例；(b)-(d)是传统的缩放方法，只增加网络宽度、深度或分辨率中的一个维度。(e)是我们提出的复合缩放方法，它以固定比例均匀缩放所有三个维度）

2、EfficientNetv1网络详解网络架构

EfficientNetv1是由谷歌团队在2019年提出的一种高效的Convolutional Neural Network (CNN)结构，旨在通过同时改变Width（宽度）、Depth（深度）和Resolution（分辨率）三个关键参数以获得最优的模型性能。 EfficientNetv1具有如下的网络架构： 输入图像 （224x224x3） Convolutional layer （3x3） Batch Normalization Swish activation MBConv blocks x n MBConv block的结构为： Depthwise Convolutional layer （3x3） Batch Normalization Swish activation Pointwise Convolutional layer (1x1) Batch Normalization Swish activation 其中MBConv表示Mobile Inverted Residual Bottleneck Block，是由两个分支组成的残差结构，其中一个分支是标准卷积层，另一个分支采用Depthwise Convolutional layer 和Pointwise Convolutional layer组成的轻量化块，以减少处理量和模型参数数量。Swish激活函数是sigmoid函数的近似，可以更好地提高准确度。 在上述MBConv blocks结构中，n代表EfficientNetv1的缩放系数，通过同时缩放Width、Depth和Resolution，可以从EfficientNet-B0到EfficientNet-B7进行选择，以逐步提高模型的深度和复杂性。 最后，EfficientNetv1中还使用了Global Average Pooling和Fully Connected layer产生模型的输出。 总体来说，EfficientNetv1的网络架构旨在通过对三个关键参数进行优化来提高模型的性能和效率，是当前在Imagenet上的性能最好的模型之一。

3.正文分析

卷积神经网络准确性:自2012年AlexNet（Krizhevsky等人）获得ImageNet比赛冠军以来，通过变得更大，卷积神经网络的准确性越来越高:虽然2014年ImageNet冠军GoogleNet（Szegedy等人，2015）使用约6.8M参数实现了74.8％的top-1准确率，但2017年ImageNet冠军SENet（Hu等人，2018）使用145M参数实现了82.7％的top-1准确率。最近，GPipe（Huang等人，2018）将ImageNet top-1验证准确性的最新水平进一步推至84.3％，使用了557M个参数：它非常大，只能通过分割网络并将每个部分分配到不同的加速器来使用专用的管道并行库进行训练。虽然这些模型主要设计用于ImageNet，但最近的研究表明，更好的ImageNet模型在各种迁移学习数据集（Kornblith等人，2019）以及其他计算机视觉任务如目标检测（He等人，2016; Tan等人，2019）中表现更好。尽管更高的准确性对许多应用至关重要，但我们已经达到了硬件内存限制，因此进一步提高准确性需要更好的效率。

 卷积神经网络的效率：深度卷积神经网络通常会超过参数化。模型压缩（韩等，2016年；何等，2018年；杨等，2018年）是一种通过牺牲准确性换取效率来减少模型大小的常见方式。随着移动手机的普及，人们也经常手工制作高效的移动大小卷积神经网络，如SqueezeNets（Iandola等，2016年；Gholami等，2018年），MobileNets（Howard等，2017年；Sandler等，2018年）和ShuffleNets（张等，2018年；马等，2018年）。最近，神经架构搜索在设计高效的移动大小卷积神经网络（谭等，2019年；蔡等，2019年）中越来越受欢迎，并通过广泛调整网络宽度、深度、卷积核类型和大小实现了比手工制作的移动卷积神经网络更好的效率。然而，如何将这些技术应用于设计空间更大、调整成本更高的大型模型仍不清楚。为了实现这一目标，本文采用模型缩放技术研究超大型卷积神经网络的效率，超过现有最先进的准确性水平。

模型缩放：对于不同的资源限制，有许多方式可以对ConvNet进行缩放：例如，ResNet（He et al。，2016）可以通过调整网络深度（#layers）进行缩小（例如，ResNet-18）或扩展（例如，ResNet-200），而WideResNet（Zagoruyko＆Komodakis，2016）和MobileNets（Howard et al。，2017）可以通过网络宽度（#channels）进行缩放。同时，更大的输入图像尺寸也被公认能提高准确性，但会增加更多的FLOPS开销。虽然之前的研究已经证明（Raghu et al。，2017；Lin＆Jegelka，2018；Sharir＆Shashua，2018；Lu et al。，2018），对于ConvNets 的表达能力，网络深度和宽度两者都很重要，但如何有效地缩放ConvNet以实现更好的效率和准确性仍然是一个开放性问题。我们的工作系统地和经验性地研究了ConvNet缩放的三个维度：网络宽度、深度和分辨率。

在这一部分中，我们将制定缩放问题，研究不同的方法，并提出我们的新的缩放方法。3.1问题阐述ConvNet层i可以被定义为函数：Yi=Fi（Xi），其中Fi是算子，Yi是输出张量，Xi是输入张量，张量形状为hHi;Wi;Cii1，其中Hi和Wi是空间维度，Ci是通道维度。ConvNet N可以通过组成层的列表来表示：N=Fk... F2 F1（X1）=Jj=1... k Fj（X1）。在实践中，ConvNet层通常被分成多个阶段，每个阶段的所有层分享相同的架构：例如，ResNet（He等，2016）有五个阶段，每个阶段的所有层都具有相同的卷积类型，除了第一层执行下采样。因此，我们可以将ConvNet定义为：N=Ki=1...s FLi ^i FLi ^i XhHi;Wi;Cii（1）其中FLi ^i FLi ^i表示第i层Fi在阶段i中重复Li次，hHi;Wi;Cii表示层i输入张量X的形状。图2（a）说明了一个典型的ConvNet，其中空间维度逐渐缩小，但通道维度在层中扩展，例如，从初始输入形状h224; 224; 3i到最终输出形状h7; 7; 512i。与大多数专注于找到最佳层架构Fi的常规ConvNet设计不同，模型缩放尝试扩展网络长度（Li）、宽度（Ci）和/或分辨率（Hi；Wi），而不改变Fi在基线网络中预定义的架构。通过固定Fi，模型缩放简化了新资源约束的设计问题，但它仍然是一个探索每个层的不同Li;Ci;Hi;Wi的大型设计空间。为了进一步减少设计空间，我们限制所有层必须以恒定比例均匀缩放。我们的目标是最大化任何给定资源约束的模型准确性，这可以被制定为一个优化问题：max d;w;r Accuracy N（d;w;r）s：t：N（d;w;r）=Ki=1...s F^d·L^i ^i Xhr·H^i;r·W^i;w·C^ii（2）记忆（N）≤目标内存FLOPS（N）≤目标flops其中w;d;'

3.2. 缩放维度 问题2的主要困难在于最佳的d;w;r互相依赖，并且在不同的资源约束下值会发生变化。由于这个困难，传统方法大多在以下几个维度缩放ConvNets：深度（d）：扩展网络深度是许多ConvNets（He等人，2016；Huang等人，2017；Szegedy等人，2015；2016）采用的最常见方法。直觉是深度的ConvNet可以捕获更加丰富和复杂的特征，并在新任务上很好地推广。然而，由于消失的梯度问题（Zagoruyko＆Komodakis，2016），更深的网络也更难以训练。尽管有一些技术，例如跳跃连接（He等人，2016）和批量归一化（Ioffe＆Szegedy，2015），可以缓解训练问题，但非常深的网络的精度增益会降低：例如，ResNet-1000的精度与ResNet-101相似，即使它有更多的层。图3（中间）显示了我们关于使用不同深度系数d缩放基线模型的经验研究，进一步表明非常深的ConvNets的精度返回有限。

宽度（w）：对于小型模型，缩放网络宽度通常被广泛使用（Howard et al., 2017; Sandler et al., 2018; Tan et al., 2019）。正如Zagoruyko和Komodakis(2016)所讨论的，更宽的网络往往能够捕捉更精细的特征并更容易训练。然而，极宽但浅的网络往往难以捕捉更高级的特征。我们在图3（左）中的实证结果表明，当网络变得更宽（即宽度w变大）时，准确度很快饱和。 分辨率（r）：对于更高分辨率的输入图像，ConvNets可以潜在地捕捉更精细的模式。从早期ConvNets的224x224开始，现代ConvNets倾向于使用299x299（Szegedy et al., 2016）或331x331（Zoph et al., 2018）以获得更好的准确性。最近，GPipe（Huang et al., 2018）使用480x480的分辨率实现了ImageNet最先进的准确性。更高的分辨率，例如600x600，在物体检测ConvNets（He等人，2017; Lin等人，2017）中也被广泛使用。图3（右）展示了缩放网络分辨率的结果，确实更高的分辨率提高了准确度，但对于非常高的分辨率（r = 1：0表示分辨率224x224，r = 2：5表示分辨率560x560），准确度的增益减小。 以上分析带给我们第一个观察结果：观察结果1-放大网络宽度、深度或分辨率中的任何一个维度都能提高准确度，但对于更大的模型，准确度的增益逐渐降低。

分辨率（r）：随着更高分辨率的输入图像，ConvNets可以潜在地捕捉到更精细的模式。从早期ConvNets的224x224开始，现代ConvNets倾向于使用299x299（Szegedy等人，2016）或331x331（Zoph等人，2018）以获得更好的准确性。最近，GPipe（Huang等人，2018）通过480x480分辨率实现了最先进的ImageNet准确性。更高的分辨率，例如600x600，在对象检测ConvNets（He等人，2017; Lin等人，2017）中也被广泛使用。图3（右）显示了网络分辨率的缩放结果，高分辨率确实提高了准确性，但对于非常高的分辨率（r = 1：0表示分辨率224x224，r = 2：5表示分辨率560x560）的准确性增益逐渐减少。以上分析带领我们到第一个观察：观察1-扩大网络宽度、深度或分辨率的任何维度都可以提高准确性，但准确性的提高对于更大的模型而言有所减弱。

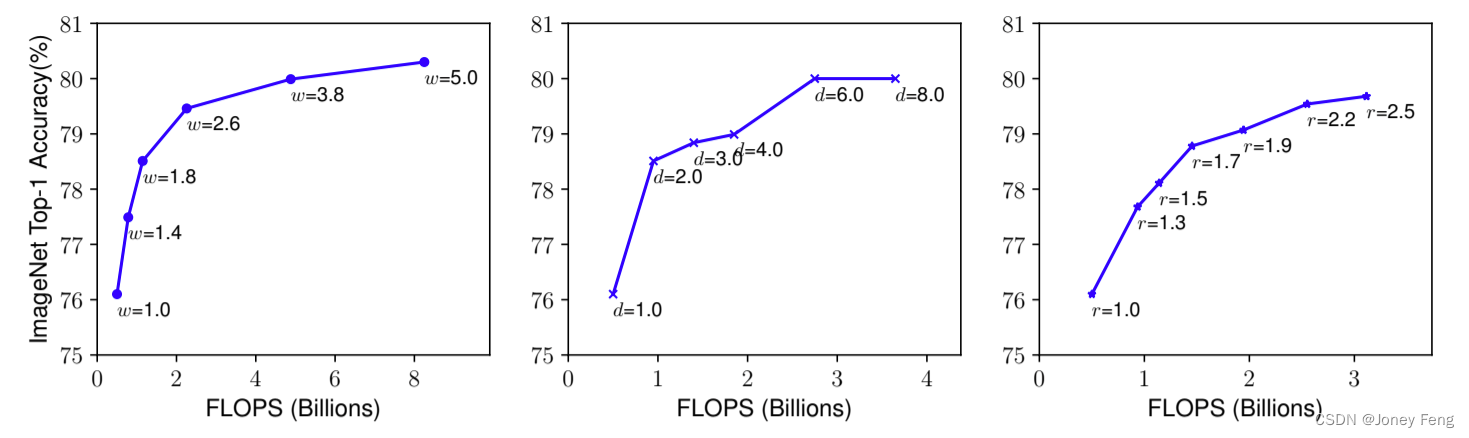
 （图3.使用不同的网络宽度（w）、深度（d）和分辨率（r）系数来扩展基线模型。具有更大宽度、深度或分辨率的大型网络倾向于实现更高的准确性，但在达到80%后，准确性增益很快饱和，显示了单一维度扩展的限制。基线网络在表1中描述）

3.3. 复合比例尺 我们从经验上观察到不同的缩放维度并不是独立的。直观地说，对于更高分辨率的图像，我们应该增加网络的深度，从而更大的感受野可以捕捉到包含更多像素的类似特征。相应地，当分辨率更高时，我们也应该增加网络的宽度，以便在高分辨率图像中捕捉到更细粒度的模式和更多的像素。这些直觉表明，我们需要协调和平衡不同的比例尺维度，而不是传统的单一维度比例尺。为了验证我们的直觉，我们比较了在不同的网络深度和分辨率下的宽度比例尺，如图4所示。如果我们只缩放网络宽度w而不改变深度（d=1.0）和分辨率（r=1.0），精度会很快饱和。在更深的（d=2.0）和更高分辨率（r=2.0）下，宽度比例尺在相同的FLOPS成本下实现了更好的精度。这些结果引导我们得出第二个观察结果：观察2 - 为了追求更好的精度和效率，在ConvNet比例尺达到平衡时，平衡所有的网络宽度、深度和分辨率是至关重要的。事实上，一些先前的工作（Zoph等，2018年；Real等，2019年）已经尝试过任意平衡网络的宽度和深度，但它们都需要繁琐的手动调整。在本文中，我们提出了一种新的复合缩放方法，它使用复合系数φ以原则性地统一缩放网络的宽度、深度和分辨率：深度：d =αφ，宽度：w =βφ，分辨率：r =γφ，使得α·β2·γ2≈2，α≥1；β≥1；γ≥1（3）。其中α、β、γ是可以通过小网格搜索确定的常数。直观地，φ是一个用户指定的系数，用于控制模型缩放所需的更多资源的数量，而α、β、γ则指定如何将这些额外资源分配到网络宽度、深度和分辨率上。值得注意的是，常规卷积运算的FLOPS与d、w2、r2成比例，即倍增网络的深度将使FLOPS倍增，但倍增网络的宽度或分辨率将使FLOPS增加四倍。由于卷积运算通常在ConvNets中占主导地位，使用方程3进行ConvNet的缩放将增加总FLOPS约为α·β2·γ2φ。在本文中，我们限制α·β2·γ2≈2，以使对于任何新的φ，总FLOPS将近似增加2φ。

（图4.不同基线网络的缩放网络宽度。线上的每个点表示具有不同宽度系数（w）的模型。所有基线网络均来自表1。第一个基线网络（d = 1.0，r = 1.0）具有18个卷积层，分辨率为224x224，而最后一个基线（d = 2.0，r = 1.3）具有36层，分辨率为299x299。）

<ol start="4"> <li>EfficientNet架构 由于模型缩放不会改变基线网络中的层操作F^i，因此拥有一个好的基线网络也是至关重要的。我们将使用现有的ConvNets来评估我们的缩放方法，但为了更好地展示我们的缩放方法的有效性，我们还开发了一个名为EfficientNet的新的移动大小基线。受（Tan et al.，2019）的启发，我们通过利用多目标神经架构搜索来优化精度和FLOPS，开发了我们的基线网络。具体而言，我们使用与（Tan et al.，2019）相同的搜索空间，并使用ACC（m）× [FLOPS（m）= T]w作为优化目标，其中ACC（m）和FLOPS（m）表示模型m的精度和FLOPS，T是目标FLOPS，w = -0.07是控制精度和FLOPS之间平衡的超参数。与（Tan et al.，2019; Cai et al.，2019）不同，我们在这里优化FLOPS而不是延迟，因为我们没有针对任何特定的硬件设备。我们的搜索产生了一个有效的网络，我们将其命名为EfficientNet-B0。由于我们使用与（Tan et al.，2019）相同的搜索空间，因此该架构类似于Mnas-Net，但由于较大的FLOPS目标（我们的FLOPS目标为400M），我们的EfficientNet-B0略微更大。表1显示了EfficientNet-B0的架构。其主要构建块是移动反向瓶颈MBConv（Sandler et al.，2018; Tan et al.，2019），我们还添加了收缩和激发优化（Hu et al.，2018）。从基线EfficientNet-B0开始，我们应用我们的复合缩放方法来进行两步缩放：•第1步：我们首先固定φ = 1，假设有两倍的资源可用，并基于公式2和3进行小型网格搜索。特别是，我们发现EfficientNet-B0的最佳值为α = 1：2；β = 1：1；γ = 1：15，在α·β2·γ2 ≈ 2的约束下。•第2步：然后固定α；β；γ为常数，并使用公式3对基线网络进行不同的φ缩放，以获得EfficientNet-B1到B7（详见表2）。值得注意的是，可以实现更好的性能。

（图5. FLOPS与ImageNet精度-类似于图1，但它比较的是FLOPS，而不是模型大小） 

 （图6. 模型参数与迁移学习准确性- 所有模型都是在ImageNet上预训练，并在新数据集上进行微调。）

实验 在这一部分，我们将首先评估我们的缩放方法对现有ConvNets和新提出的EfficientNets的影响。 5.1. 将MobileNets和ResNets放大 作为概念验证，我们首先将我们的缩放方法应用于广泛使用的MobileNets（Howard等人，2017; Sandler等人，2018）和ResNet（He等人，2016）。表3显示了按不同方式缩放它们的ImageNet结果。与其他单一维度缩放方法相比，我们的复合缩放方法提高了所有这些模型的准确性，表明我们所提出的通用现有ConvNets缩放方法的有效性。

le 3.5.2 EfficientNet在ImageNet上的结果 我们在ImageNet上训练了EfficientNet模型，使用了与(Tan et al.，2019)类似的设置：RMSProp优化器，衰减率为0.9和动量为0.9; 批归一化动量为0.99; 权重衰减为1e-5; 初始学习率为0.256，每2.4个周期衰减0.97。我们还使用了SiLU（Swish-1）激活（Ramachandran等人，2018; Elfwing等人，2018; Hendrycks＆Gimpel，2016）、AutoAugment（Cubuk等人，2019）和随机深度（Huang等人，2016），生存概率为0.8。众所周知，更大的模型需要更多的正则化，我们从EfficientNet-B0的0.2线性增加了Dropout（Srivastava等人，2014）比率到B7的0.5。我们从训练集中随机选择了25K张图像作为minival集合，并对此minival进行提前停止；然后我们在原始验证集上评估提前停止的检查点以报告最终的验证精度。表2显示了所有从相同基准EfficientNet-B0缩放的EfficientNet模型的性能。我们的EfficientNet模型通常使用比其他类似精度的ConvNet少一个数量级的参数和FLOPS。特别是，我们的EfficientNet-B7通过使用66M的参数和37B FLOPS实现了84.3％top1的准确率，比之前最佳的GPipe（Huang等人，2018）更准确但更小8.4倍。这些增益来自更好的架构、更好的缩放和更好的训练设置，这些设置都是针对EfficientNet定制的。图1和图5说明了代表性ConvNets的参数-精度和FLOPS-精度曲线，其中我们缩放的EfficientNet模型使用比其他ConvNets更少的参数和FLOPS实现更高的准确性。值得注意的是，我们的EfficientNet模型不仅小，而且计算更便宜。例如，我们的EfficientNet-B3使用18倍的FLOPS比ResNeXt-101（Xie等人，2017）实现了更高的准确率。为了验证延迟，我们还在真实CPU上测量了一些代表性CovNets的推理延迟，如表3所示。

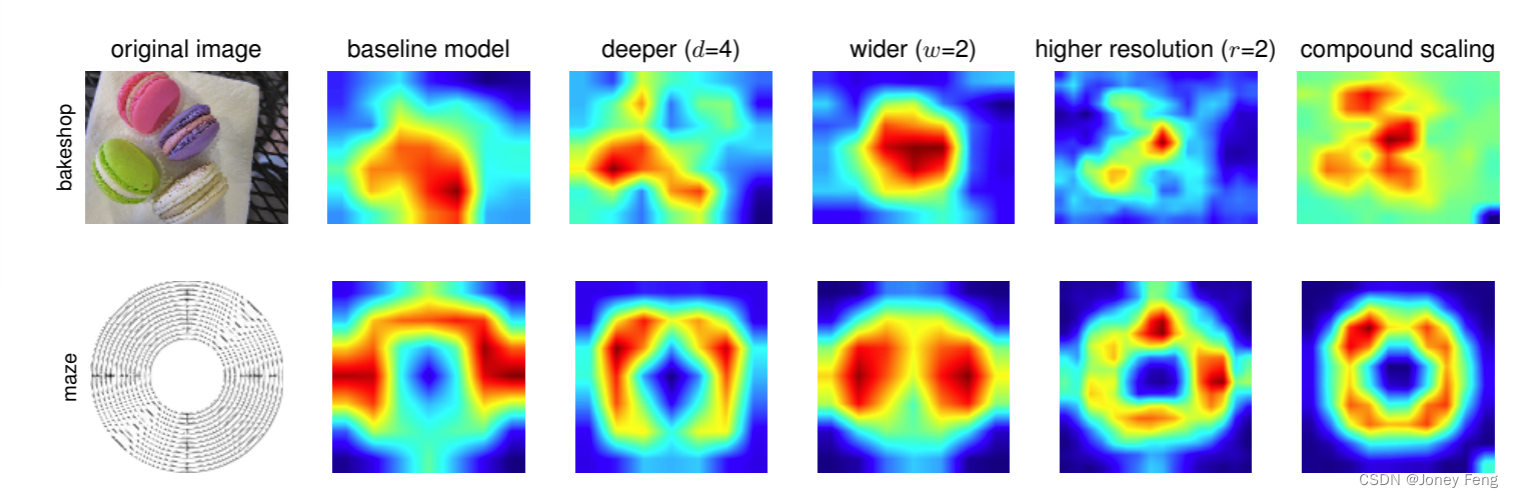
 （图7.不同缩放方法模型的类激活图(CAM)(Zhou等人，2016)-我们的复合缩放方法使得缩放模型(最后一列)能够聚焦于更具有物体细节的更相关区域。模型细节在表7中）

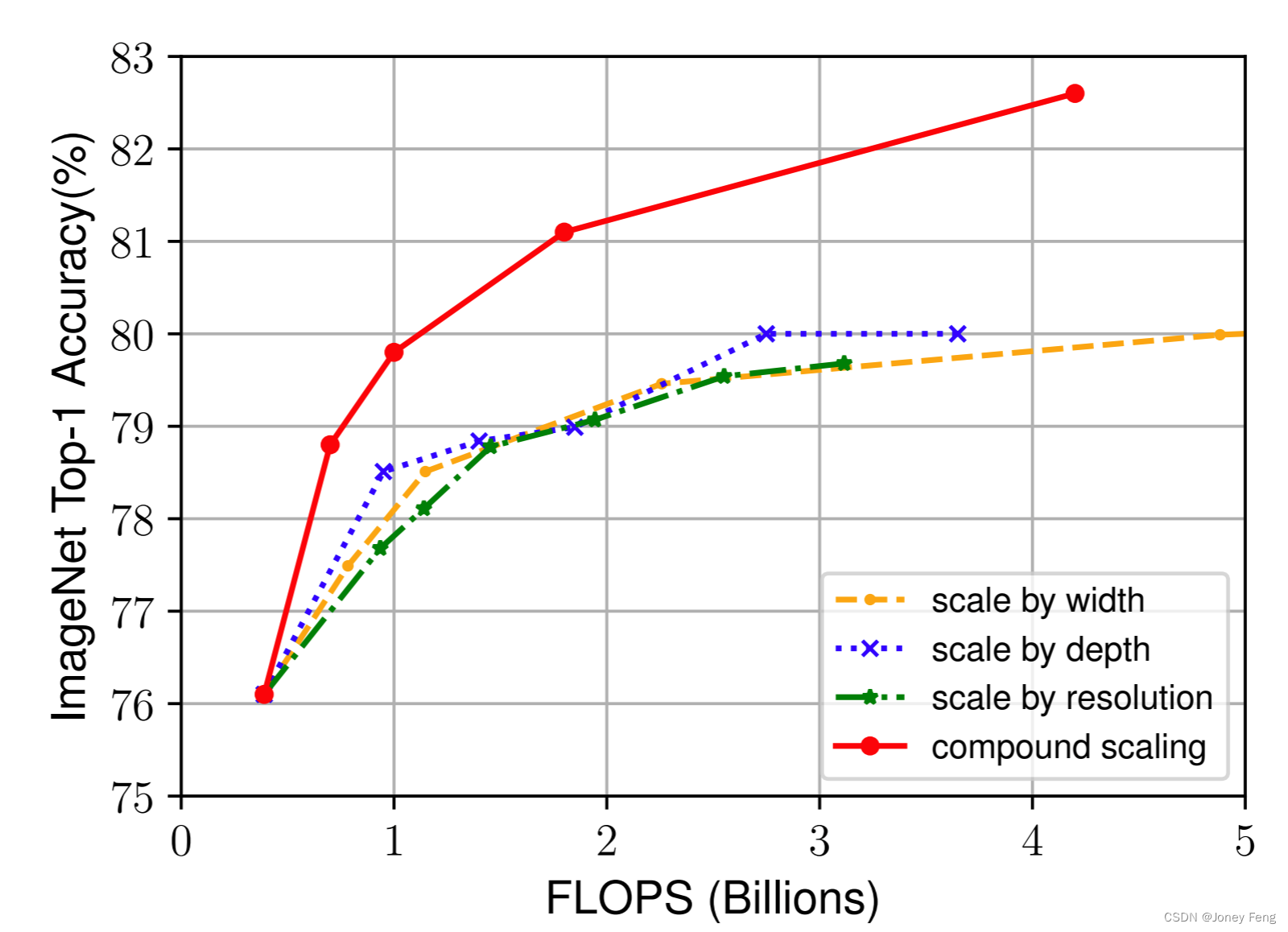
 （图8.使用不同方法扩展EfficientNet-B0的规模）

5.3. EfficientNet的迁移学习结果 我们还在一系列常用的迁移学习数据集上评估了我们的EfficientNet，如表6所示。我们借鉴了（Kornblith等人，2019）和（Huang等人，2018）的相同训练设置，即采用ImageNet预训练检查点并微调新的数据集。表5显示了迁移学习的性能：（1）与NASNet-A（Zoph等人，2018）和Inception-v4（Szegedy等人，2017）等公开可用的模型相比，我们的EfficientNet模型在平均参数减少4.7倍（高达21倍）的情况下实现了更高的准确性。 （2）与动态合成训练数据的DAT（Ngiam等人，2018）和使用专门的管道并行训练的GPipe（Huang等人，2018）等最先进的模型相比，在8个数据集中，我们的EfficientNet模型仍然在5个数据集中超越它们的准确性，但使用了少9.6倍的参数。图6比较了各种模型的准确性-参数曲线。总的来说，我们的EfficientNets在拥有一个数量级更少的参数的情况下，始终可以达到比现有模型包括ResNet（He等人，2016），DenseNet（Huang等人，2017），Inception（Szegedy等人，2017）和NASNet（Zoph等人，2018）更好的准确性。

6.讨论为了分离我们所提出的缩放方法与EfficientNet架构的贡献，图8比较了相同EfficientNet-B0基准网络的不同缩放方法的ImageNet性能。总的来说，所有的缩放方法都能够提高准确率，但代价是更高的FLOPS，但我们的复合缩放方法可以进一步提高准确率，最高可比其他单一维度的缩放方法提高2.5%，表明我们所提出的复合缩放方法的重要性。为了进一步了解为什么我们的复合缩放方法比其他方法更好，图7比较了几个具有不同缩放方法的代表模型的类激活图(Zhou等人，2016)。所有这些模型都是从同一个基线模型进行缩放的，它们的统计数据显示在表7中。图像是从ImageNet验证集中随机选取的。如图所示，使用复合缩放方法的模型倾向于关注更多相关区域的对象细节，而其他模型要么缺乏对象细节，要么无法捕捉图像中的所有对象。

1.EfficientNetv1.py(pytorch实现）

from typing import List, Callable
import torch
from torch import Tensor
import torch.nn as nn

def channel_shuffle(x:Tensor, groups:int) -> Tensor:
    batch_size, num_channels, height, width = x.size()
    channel_per_group = num_channels // groups
    x = x.view(batch_size, groups, channel_per_group, height, width)
    x = torch.transpose(x, 1, 2).contiguous()
    x = x.view(batch_size, -1, height, width)
    return x

class InvertedResidual(nn.Module):
    def __init__(self, input_c: int, output_c:int, stride:int):
        super(InvertedResidual, self).__init__()
        if stride not in [1, 2]:
            raise ValueError("illegal stride value.")
        self.stride = stride
        assert output_c % 2 == 0
        branch_features = output_c // 2
        assert (self.stride != 1) or (input_c == branch_features << 1)
        if self.stride == 2:
            self.branch1 = nn.Sequential(
                self.depthwise_conv(input_c, input_c, kernel_s=3, stride=self.stride, padding=1),
                nn.BatchNorm2d(input_c),
                nn.Conv2d(input_c, branch_features, kernel_size=1, stride=1, padding=0, bias=False),
                nn.BatchNorm2d(branch_features),
                nn.ReLU(inplace=True)
            )
        else:
            self.branch1 = nn.Sequential()
        self.branch2 = nn.Sequential(
            nn.Conv2d(input_c if self.stride > 1 else branch_features, branch_features, kernel_size=1,
                      stride=1, padding=0, bias=False),
            nn.BatchNorm2d(branch_features),
            nn.ReLU(inplace=True),
            self.depthwise_conv(branch_features, branch_features, kernel_s=3, stride=self.stride, padding=1),
            nn.BatchNorm2d(branch_features),
            nn.Conv2d(branch_features, branch_features, kernel_size=1, stride=1, padding=0, bias=False),
            nn.BatchNorm2d(branch_features),
            nn.ReLU(inplace=True)
        )

    @staticmethod
    def depthwise_conv(input_c: int,
                        output_c:int,
                        kernel_s:int,
                        stride:int=1,
                        padding:int=0,
                        bias:bool=False) -> nn.Conv2d:
        return nn.Conv2d(in_channels=input_c, out_channels=output_c, kernel_size=kernel_s,
                            stride=stride, padding=padding, bias=bias, groups=input_c)

    def forward(self, x: Tensor) -> Tensor:
        if self.stride == 1:
            x1, x2 = x.chunk(2, dim=1)
            out = torch.cat((x1, self.branch1(x), self.branch2(x)), dim=1)
        else:
            out = torch.cat((self.branch1(x), self.branch2(x)), dim=1)
        out = channel_shuffle(out, 2)
        return out

class ShuffleNetV2(nn.Module):
    def __int__(self,
                stages_repeats: List[int],
                stages_out_channels: List[int],
                num_classes:int=1000,
                inverted_residual: Callable[..., nn.Module] = InvertedResidual):
        super(ShuffleNetV2, self).__init__()
        if len(stages_repeats) != 3:
            raise ValueError("expected stages_repeats as list of 3 positive ints")
        if len(stages_out_channels) != 5:
            raise ValueError("expected stage_out_channels as list of 5 positive ints")
        self._stage_out_channels = stages_out_channels
        input_channels=3,
        output_channels = self._stage_out_channels[0]
        self.conv1 = nn.Sequential(
            nn.Conv2d(input_channels, output_channels, kernel_size=3, stride=2, padding=1, bias=False),
            nn.BatchNorm2d(output_channels),
            nn.ReLU(inplace=True)
        )
        input_channels = output_channels
        self.maxpoool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
        self.stage2:nn.Sequential
        self.stage3:nn.Sequential
        self.stage4:nn.Sequential
        stages_names = ["stage{}".format(i) for i in [2, 3, 4]]
        for name, repeats, output_channels in zip(stages_names, stages_repeats, stages_out_channels[1:]):
            seq = [inverted_residual(input_channels, output_channels, 2)]
            for i in range(repeats - 1):
                seq.append(inverted_residual(output_channels, output_channels, 1))
            setattr(self, name, nn.Sequential(*seq))
            input_channels = output_channels
        output_channels = self._stage_out_channels[-1]
        self.conv5 = nn.Sequential(
            nn.Conv2d(input_channels, output_channels, kernel_size=1, stride=1, padding=0, bias=False),
            nn.BatchNorm2d(output_channels),
            nn.ReLU(inplace=True)
        )
        self.fc = nn.Linear(output_channels, num_classes)

    def _forward_impl(self, x:Tensor) -> Tensor:
        x = self.conv1(x)
        x = self.maxpoool(x)
        x = self.stage2(x)
        x = self.stage3(x)
        x = self.stage4(x)
        x = self.conv5(x)
        x = x.mean([2, 3])
        x = self.fc(x)
        return x
    def forward(self, x:Tensor) -> Tensor:
        return self._forward_impl(x)

def shufflenet_v2_x0_5(num_classes=1000):
    model = ShuffleNetV2(stages_repeats=[4, 8, 4],
                         stages_out_channels=[24, 48, 96, 192, 1024],
                         num_classes=num_classes)
    return model

def shufflenet_v2_x1_0(num_classes=1000):
    model = ShuffleNetV2(stages_repeats=[4, 8, 4],
                         stages_out_channels=[24, 116, 232, 464, 1024],
                         num_classes=num_classes)
    return model

def shufflenet_v2_x1_5(num_classes=1000):
    model = ShuffleNetV2(stages_repeats=[4, 8, 4],
                         stages_out_channels=[24, 176, 352, 704, 1024],
                         num_classes=num_classes)
    return model

def shufflenet_v2_x2_0(num_classes=1000):
    model = ShuffleNetV2(stages_repeats=[4, 8, 4],
                         stages_out_channels=[24, 244, 488, 976, 2048],
                         num_classes=num_classes)
    return model

总结

结论 在本文中，我们系统地研究了ConvNet的规模问题，并发现仔细平衡网络的宽度、深度和分辨率是一个重要但缺失的部分，使我们无法获得更好的准确性和效率。为了解决这个问题，我们提出了一种简单而高效的复合缩放方法，它使我们能够更有原则地将基准ConvNet扩展到任何目标资源限制，同时保持模型的效率。通过这种复合缩放方法的支持，我们展示了一个移动大小的EfficientNet模型可以非常有效地扩展，比ImageNet和五个常用的迁移学习数据集上的最新准确性提高了一个数量级，同时参数和FLOPS少得多。