写的不好，见谅~
目录
概念理解
红黑树规则
AVL树与红黑树的相爱相杀
红黑树的插入时的上色与旋转。
不上色（shǎi）
情况一：空树
情况二：非空树，父节点为黑
上色（shǎi）
情况三：非空树，父节点为红色只需染色操作
上色+旋转
情况四：单旋
情况五：双旋情况
概念理解
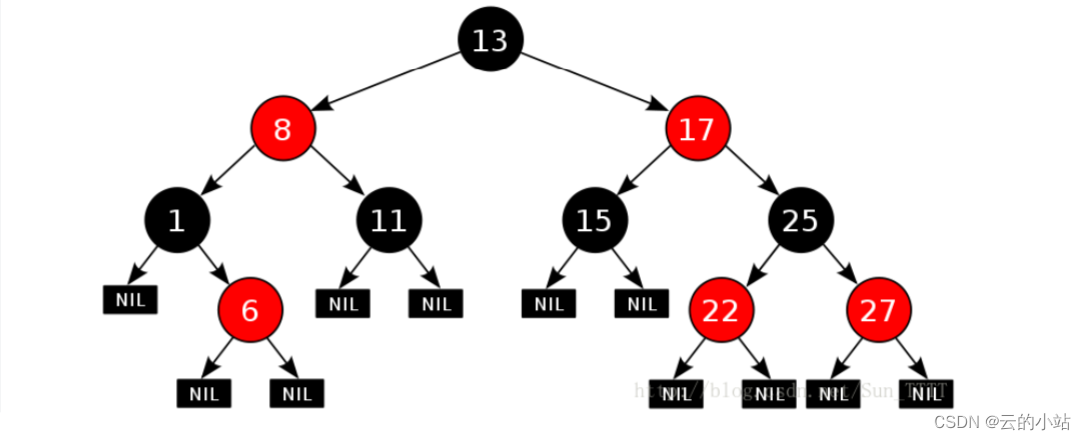
红黑树红黑树，当然是红色和黑色的结点啦。
确实，我们的红黑树的各个结点中存放着一个标志颜色的标识。
template <class T>
struct RBTreeNode//红黑树结点
{
RBTreeNode<T>* _left;//红黑树是一个三叉链的树形结构。
RBTreeNode<T>* _right;
RBTreeNode<T>* _parent;
Colour _col;//<-------颜色标识
T _data; //数据的存放
RBTreeNode(const T&data= T())
:_data(data)
, _left(nullptr)
, _right(nullptr)
,_parent(nullptr)
,_col(RED)
{}
};红黑树规则
红黑树既然是属于较为难的数据结构，那么他肯定也有着一些自己的树形规则。
在继承搜索二叉树的规则下自己新的规则如下
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的，则它的两个孩子结点是黑色的
- 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
第1、2、3点都应该看得懂吧？
先解释我们的规则5（其实可有可无的）：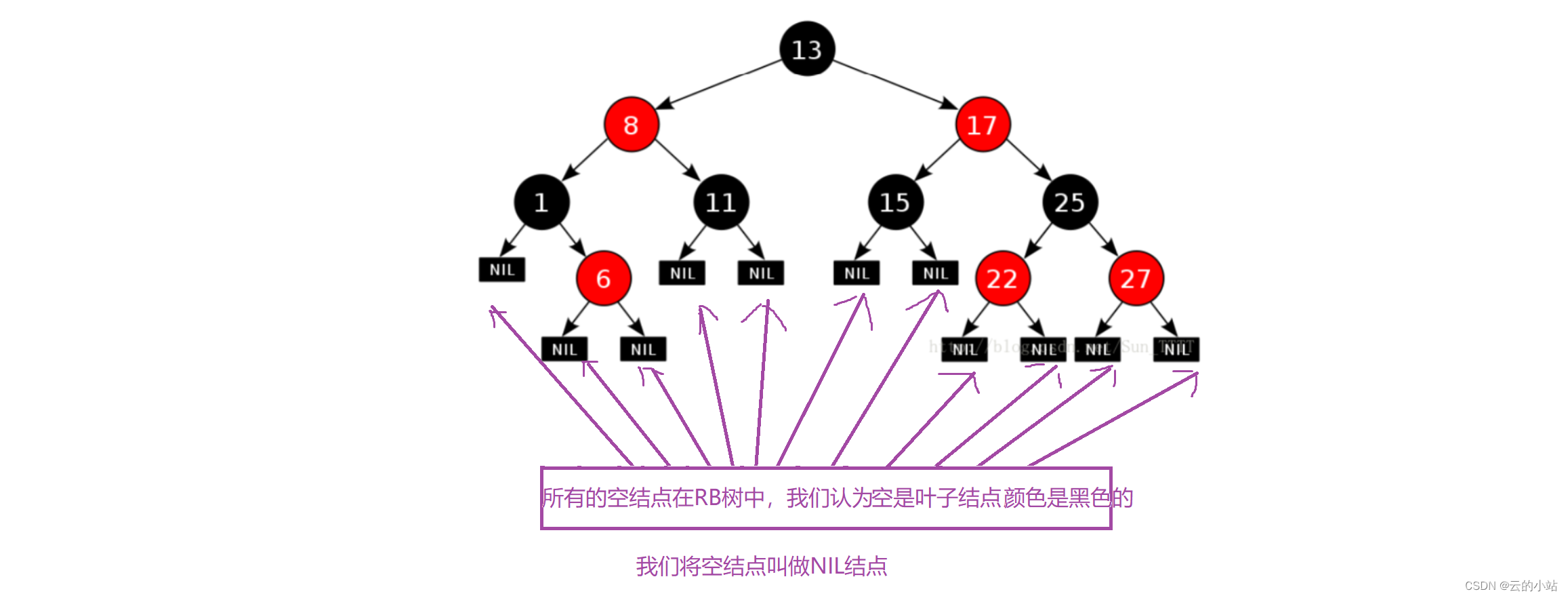
第四点规则的意思是从任意一个结点开始计算，到叶子结点的黑色结点都相同。
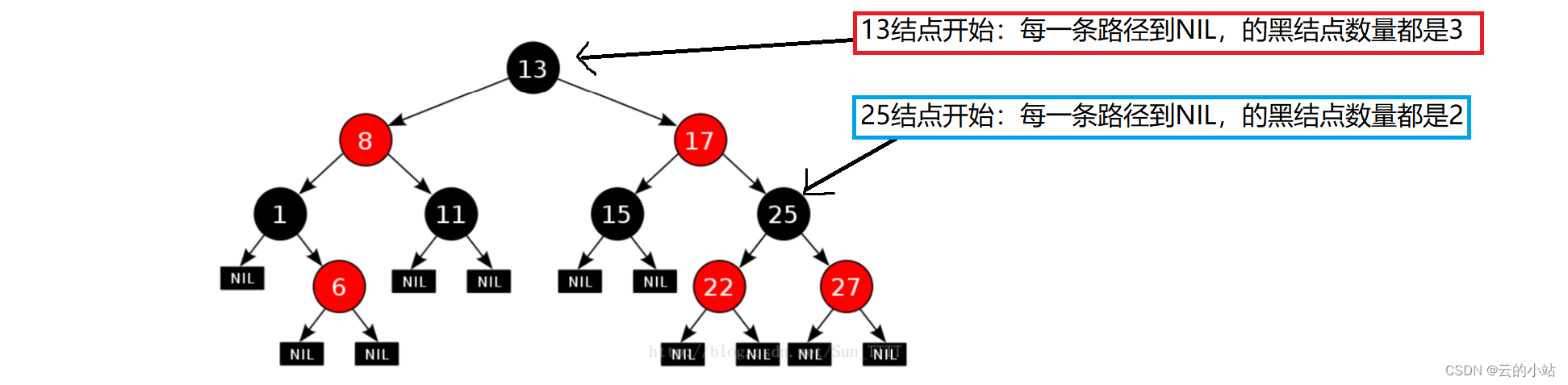
为什么要定这些规则呢？应为这些规则保证了我们的最长路径不超过最短路径的2倍。黑色结点可以连续。
AVL树与红黑树的相爱相杀
不能说红黑树是AVL树的升级版本，打个比方吧：AVL树属于严厉的高中老师，红黑树属于慈爱的小学语文老师，啊怀念她。
AVL树只要不是一就要立刻旋转该树的结构。
红黑树给我们扩大了他的高低容忍差。
向下面哪个情况，AVL树早就不知道旋转多少次了。
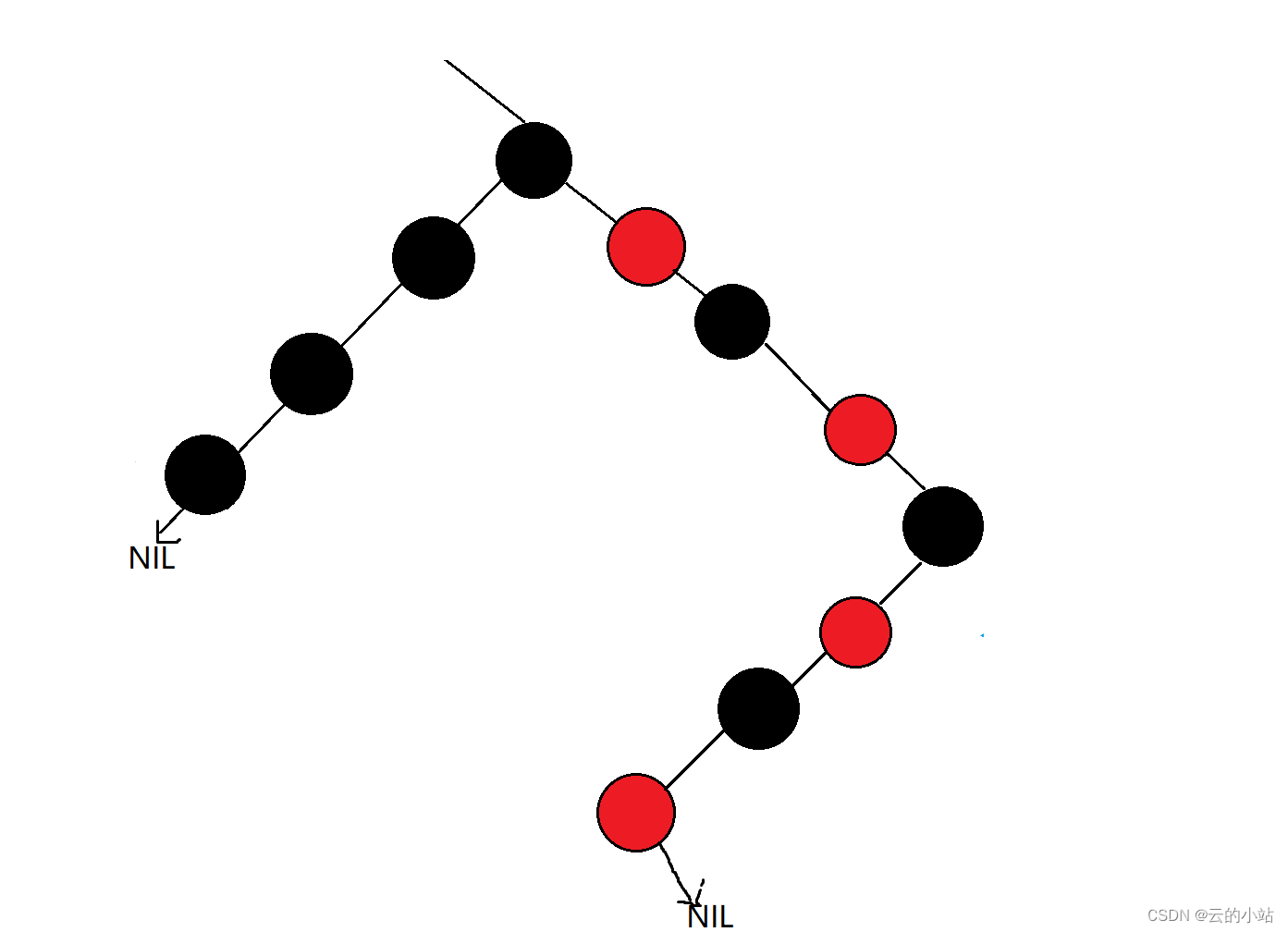
但是红黑树就是可以容忍。
AVL树和红黑树的区别如下
- AVL树是更加严格的平衡，因此可以提供更快的查找速度，一般读取查找密集型任务，适用AVL树。
- 红黑树更适合于插入修改密集型任务。
- 相对于要求严格平衡的AVL树来说，红黑树的旋转次数少，对于插入、删除操作较多的情况下，选择红黑树。
- 红黑树的查询性能略微逊色于AVL树，但是红黑树在插入和删除上优于AVL树。
红黑树的插入时的上色与旋转。
前面插入位置寻找的逻辑与搜索二叉树逻辑一样
ret_type Insert(const T& data)
{
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
return make_pair(iterator(_root), true);
}
else
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
parent = cur;
if (kot(cur->_data) > kot(data))
{
cur = cur->_left;
}
else if (kot(cur->_data) < kot(data))
{
cur = cur->_right;
}
else
{
return make_pair(iterator(cur), false);
}
}
cur = new Node(data);
Node* ret = cur;
if (kot(parent->_data) < kot(cur->_data))
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
//准备上色旋转
这上色就有讲究了！
我本以为吕布(AVL树)就天下无敌了，此人是谁的部将（红黑树）。
不上色（shǎi）
为了不会一插入就挨打，我们新结点初始状态就是红结点，为什么不是黑色呢？
如果我们插入黑色，在这棵树中有极大可能让这条路径比其他路径多一个黑色结点严重破坏结构，还得去检查前提路径黑结点情况，各种修改，各种调整，极其复杂。
所以我们都是默认新结点是红色结点，我们只需要检查脑袋上的父亲结点的颜色。
情况一：空树
那么我们的插入就是根结点，改变一下，_root链接，然后变个色就好了。
情况二：非空树，父节点为黑
这也很爽，由于父亲是黑色，我们插入一个红色结点不会破坏如何规则。
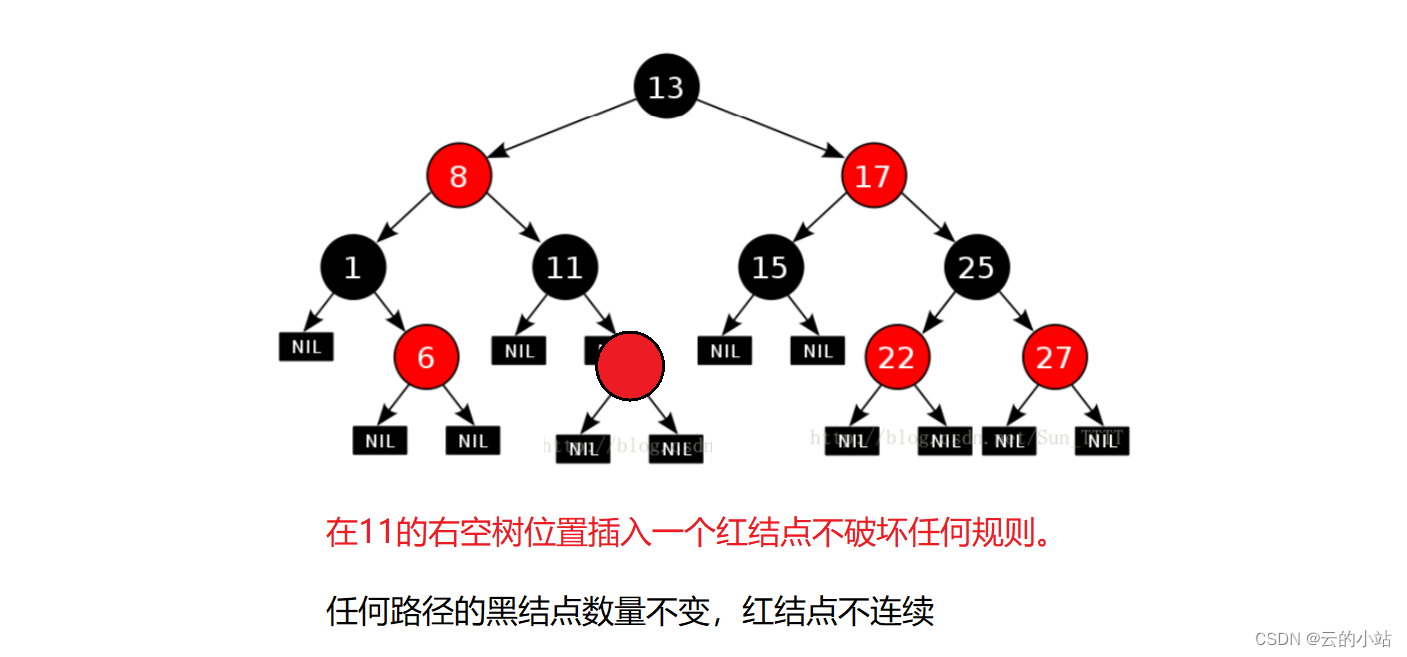
上色（shǎi）
情况三：非空树，父节点为红色只需染色操作
开始操作
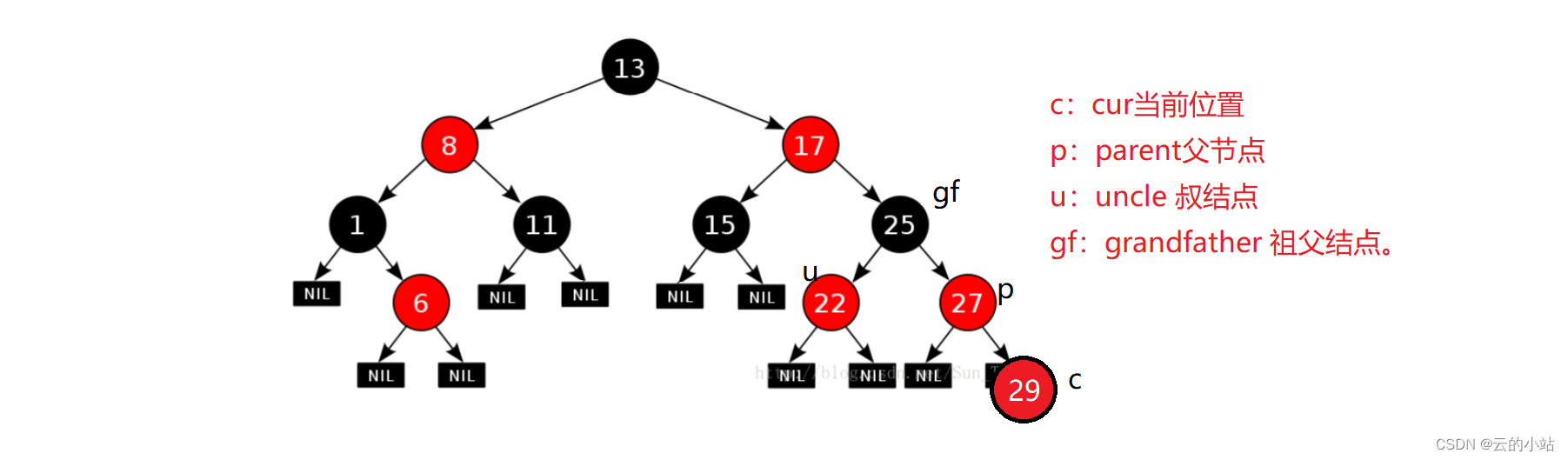
cur为刚刚插入的结点，父节点为红，我们需要检查uncle结点为红色，我们将parent和uncle染成黑色保证父节点与uncle结点所在的子树黑数量相同
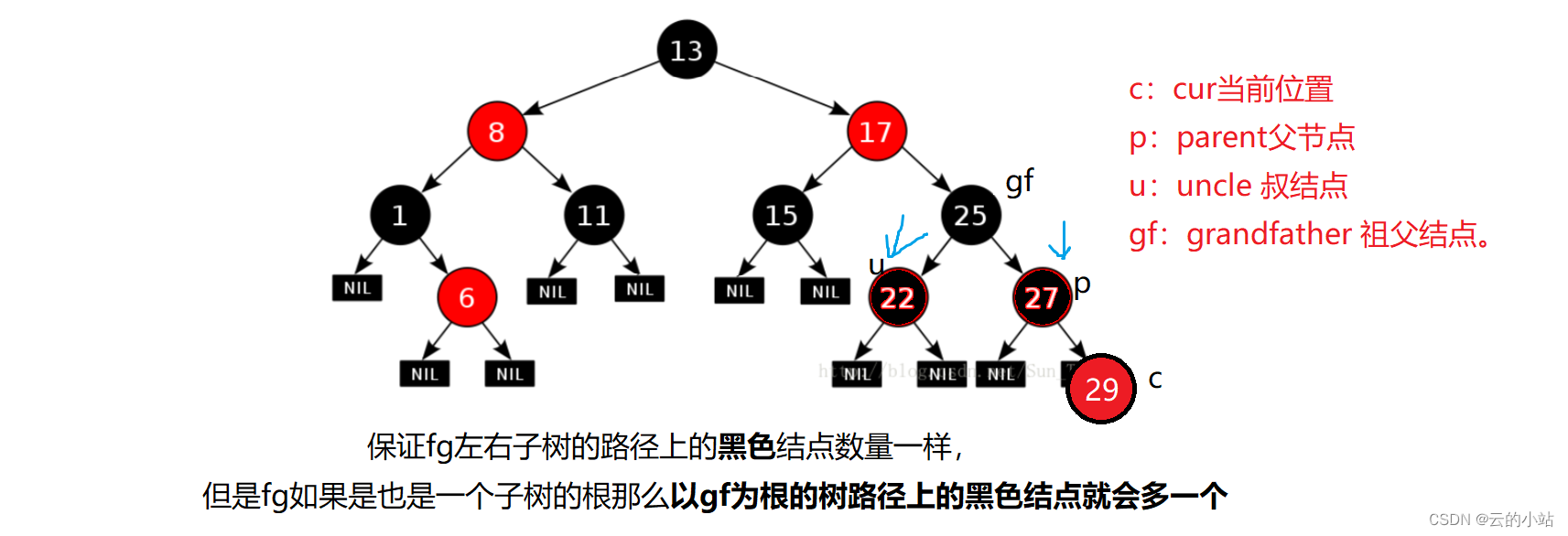我们还需要将gf染成红色，保证了17结点的左右子树路径黑色结点相同
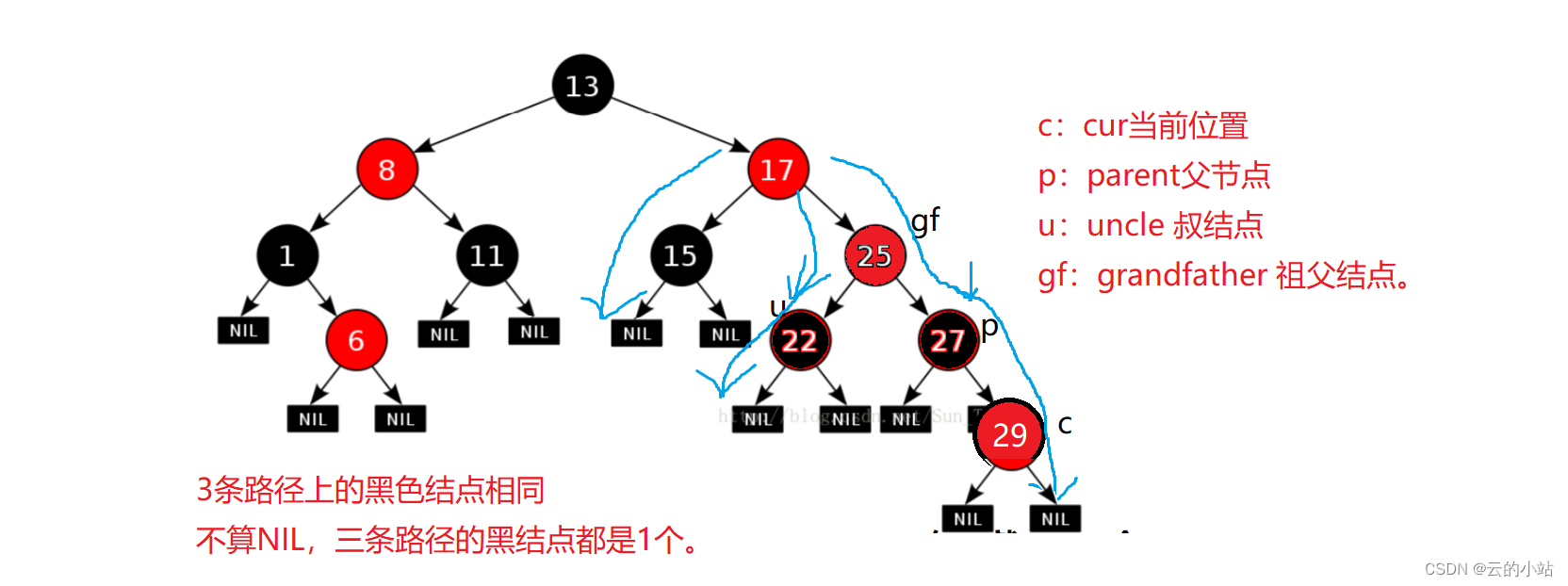
将gf指针赋给cur指针，其指针也一起变动。
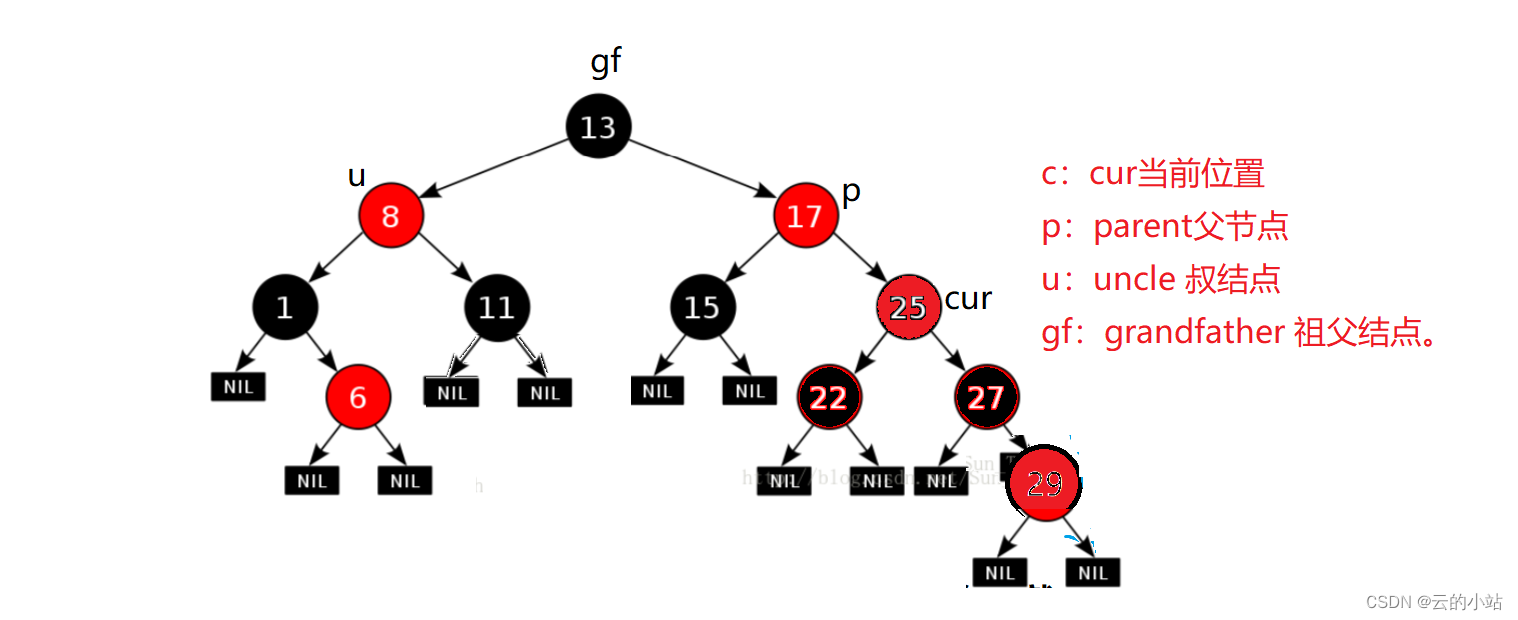
如果cur->_parent为黑色就结束，p为红色就重复之前动作
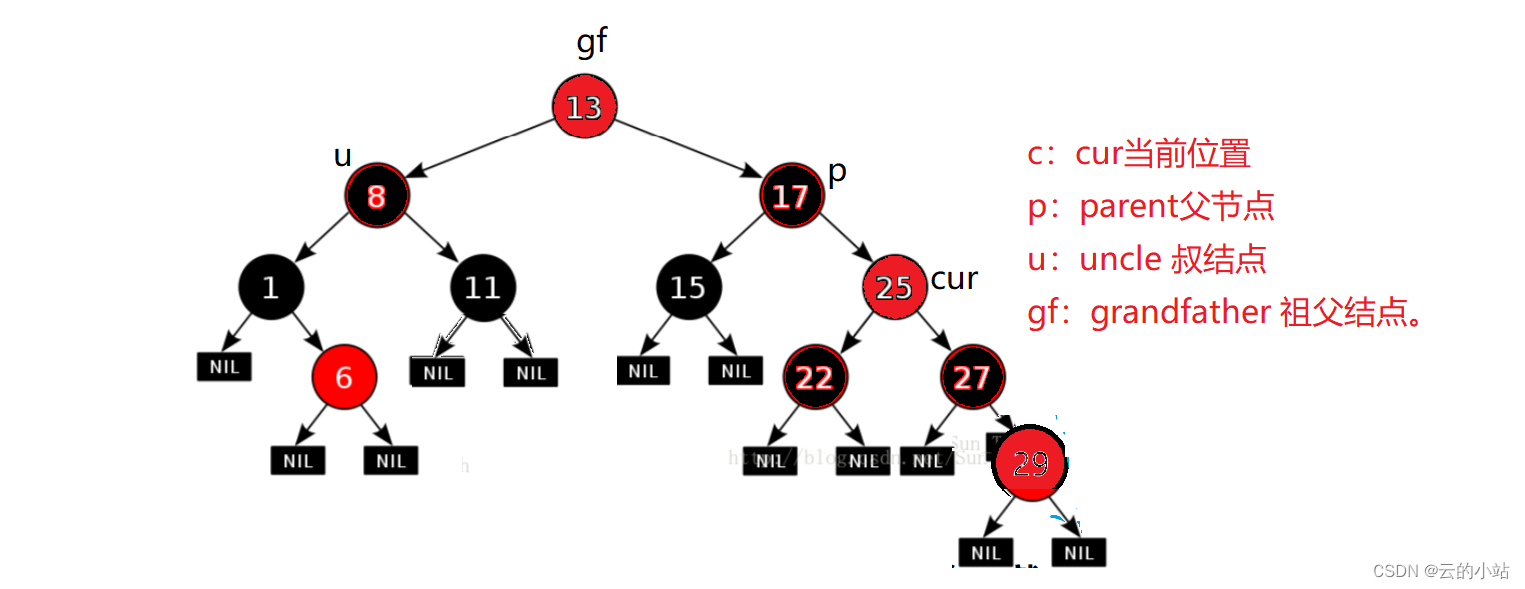
parent等于空的时候退出循环。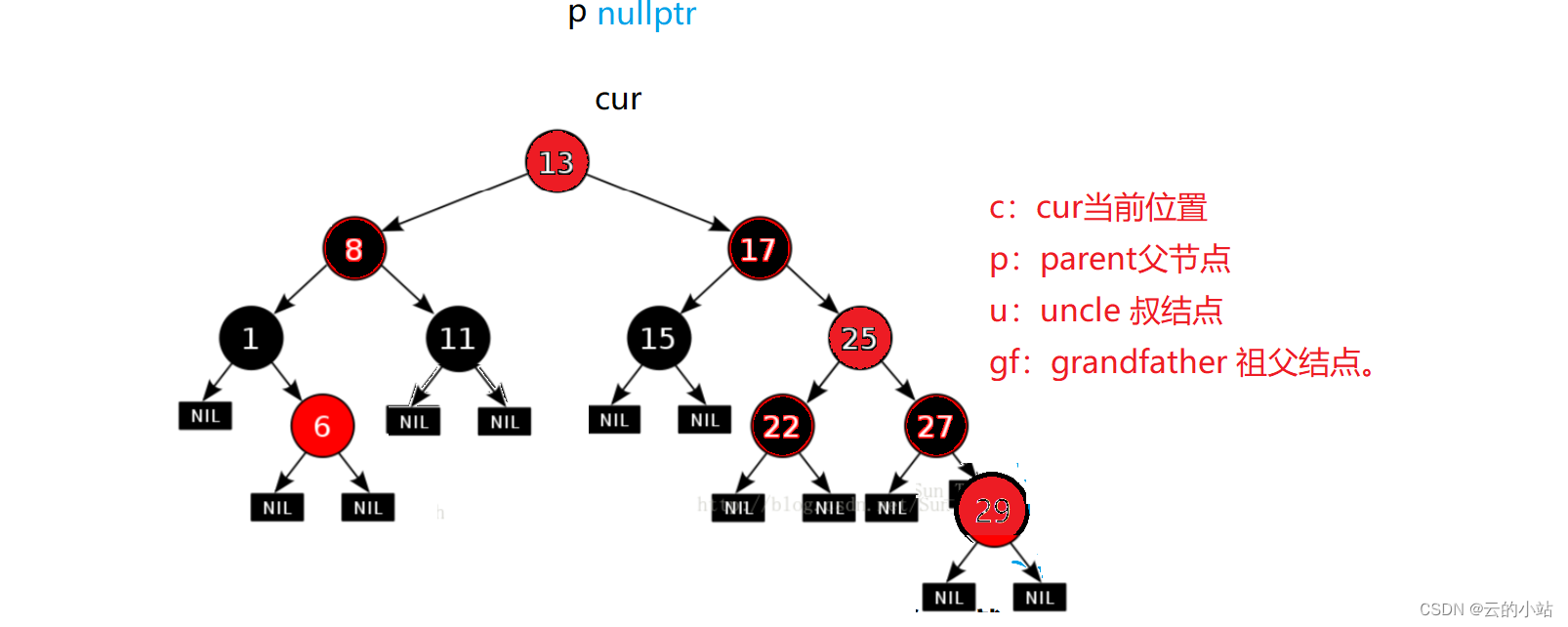
无论是哪种情况，我们最好在循环后都加上一句_root=_col=BLACK，保证大树根为黑。
while (parent && parent->_col == RED)
{
}
_root->_col = BLACK;上色+旋转
记住我们的uncle结点是很重要的，他是判别旋转的一个标志。
假设我们在上色的过程中uncle结点原本为空或者黑色的那可就麻烦了。
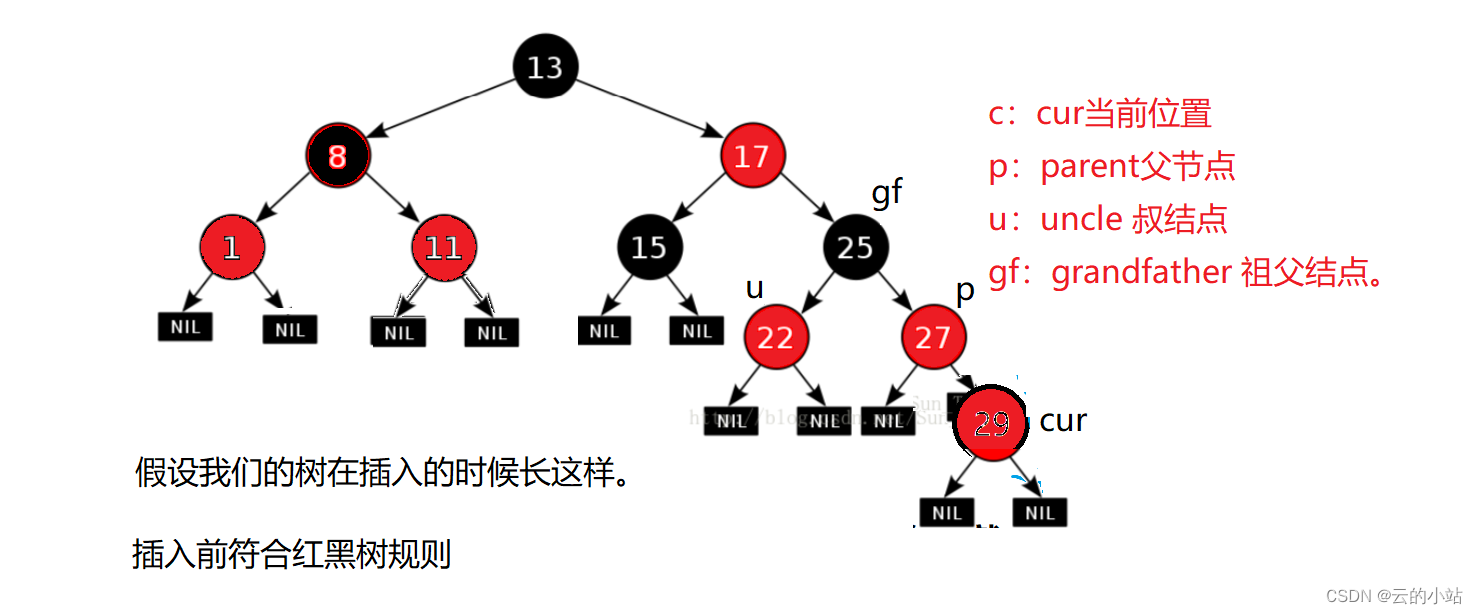
第一次上色uncle为红允许改变。
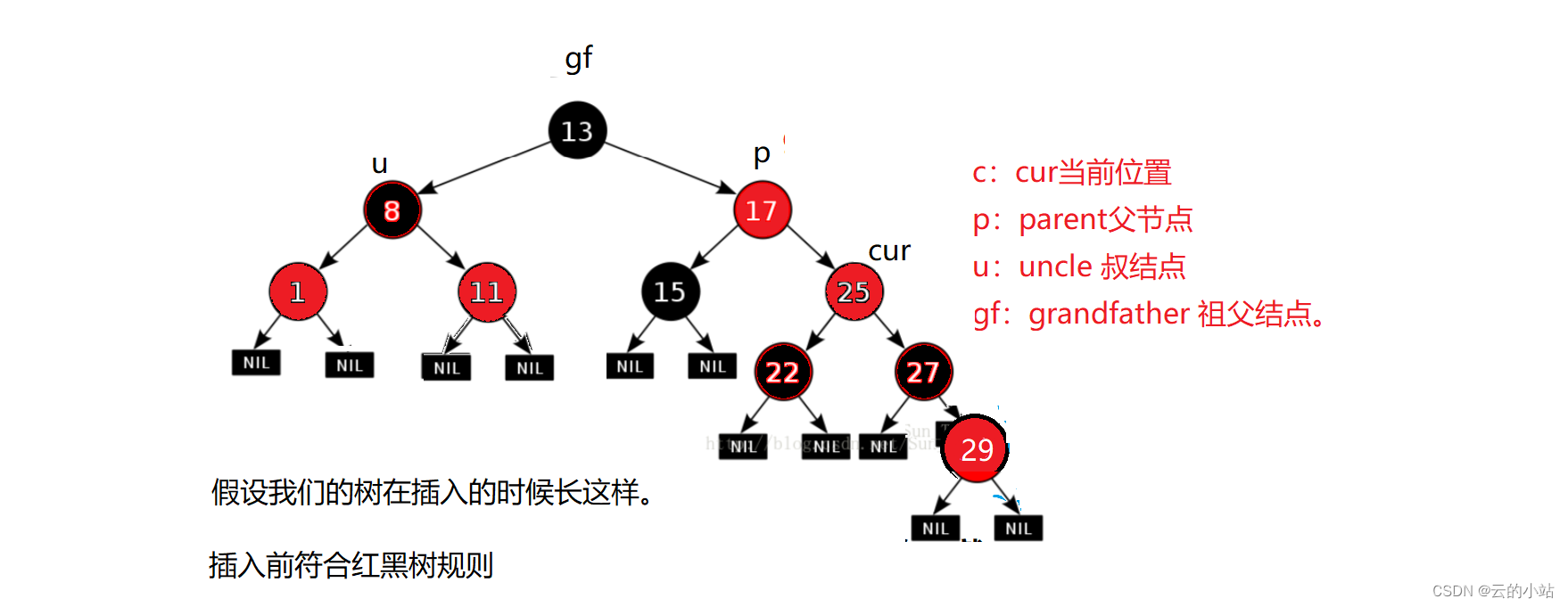
到了我们第二次操作的时候发现我们的parent为红色需要调整，但是uncle却是黑色的，不可以直接色，应为当前的gf开始每一条路径的黑结点数量都相同，如果我们一意孤行只改变p的颜色的话，会发现gf的左树路径比右数路径上的黑节点多一个，这是极其不正确的！破坏了红黑树的路径黑结点数量相同的原则。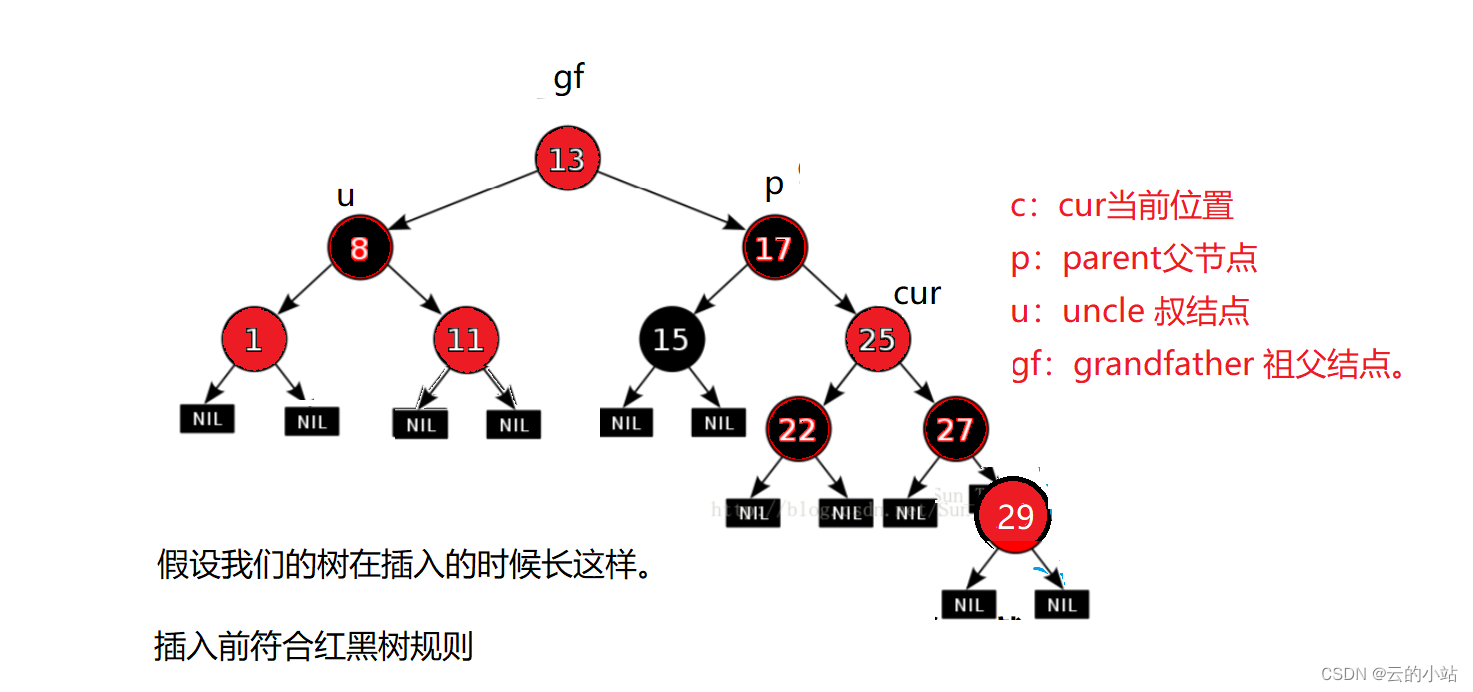
我们需要开始旋转了，根据cur确定是双旋还是单旋。图里的是左单选情况。
情况四：单旋
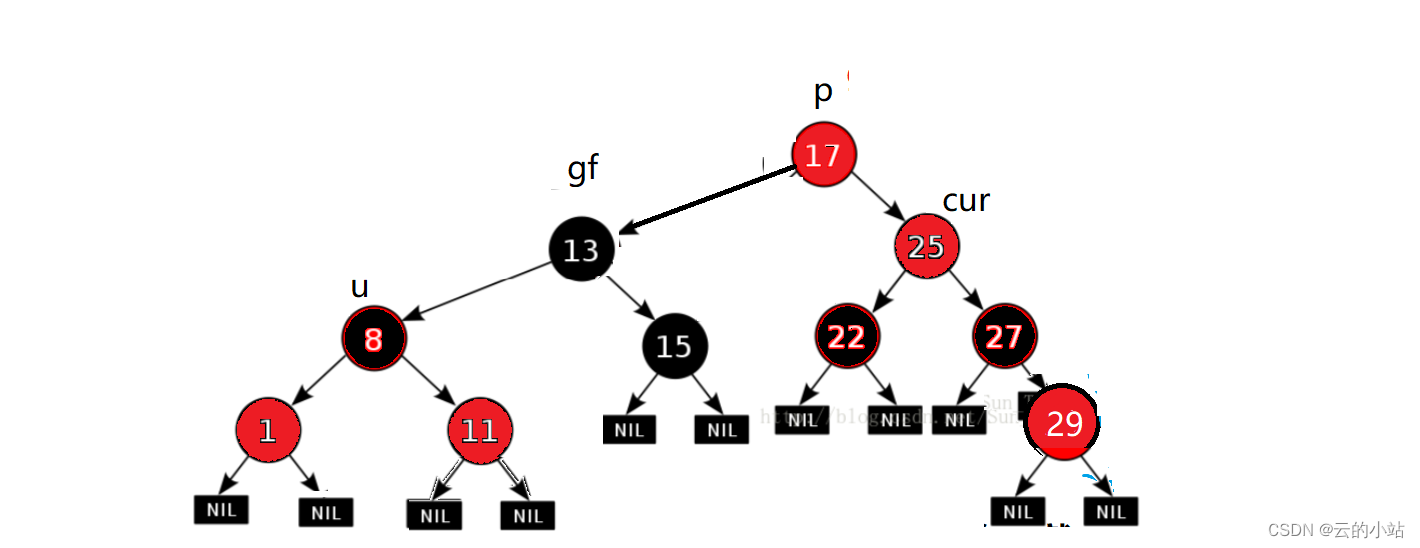
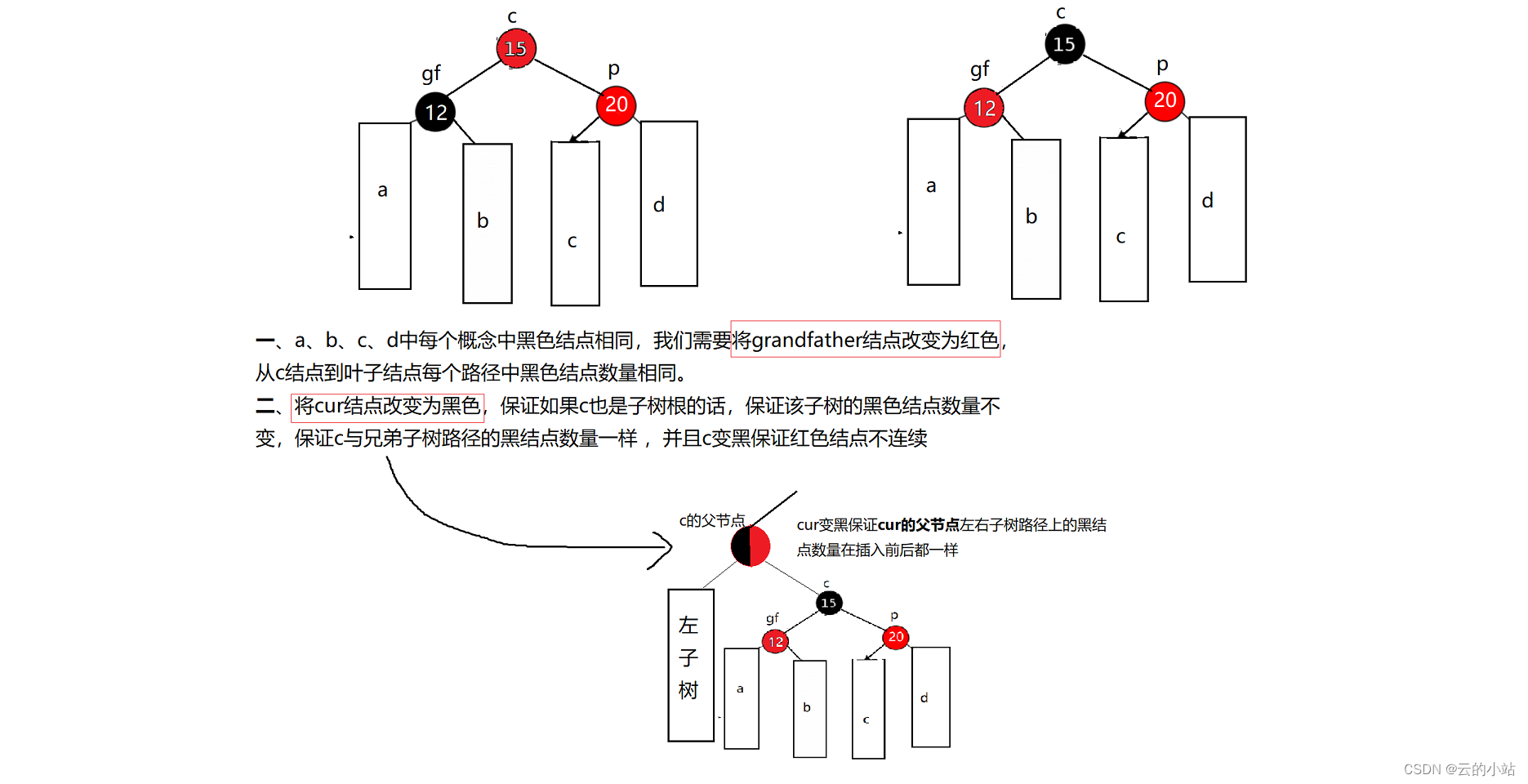
旋转完后为了防止我们所看见的树也是一颗子树，我们恢复到旋转前黑色结点差，并且遵守规则，我们将p的颜色改变为BLACK，将gf改变为RED，
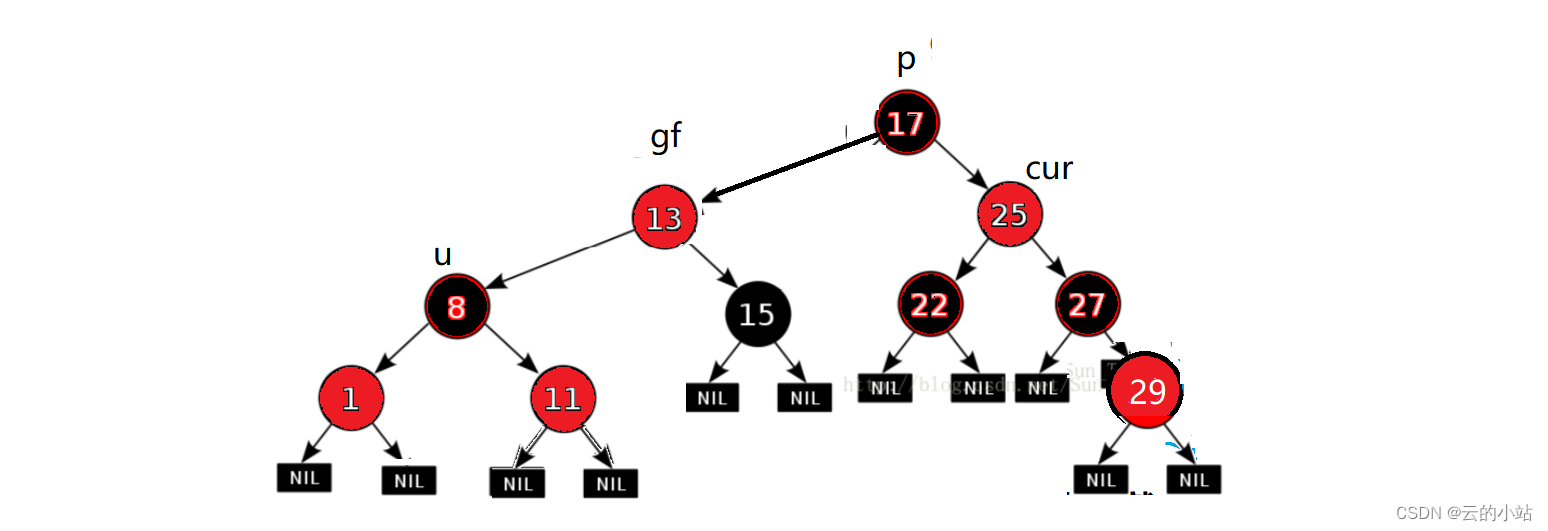
这样哪怕这就是是整颗红黑树，那他的根也是黑的，如果他只是红黑树的一个子树，我们的在各个路径上黑色结点的数量在插入后也是不改变的：插入前2个黑色结点，插入后依旧是2个。
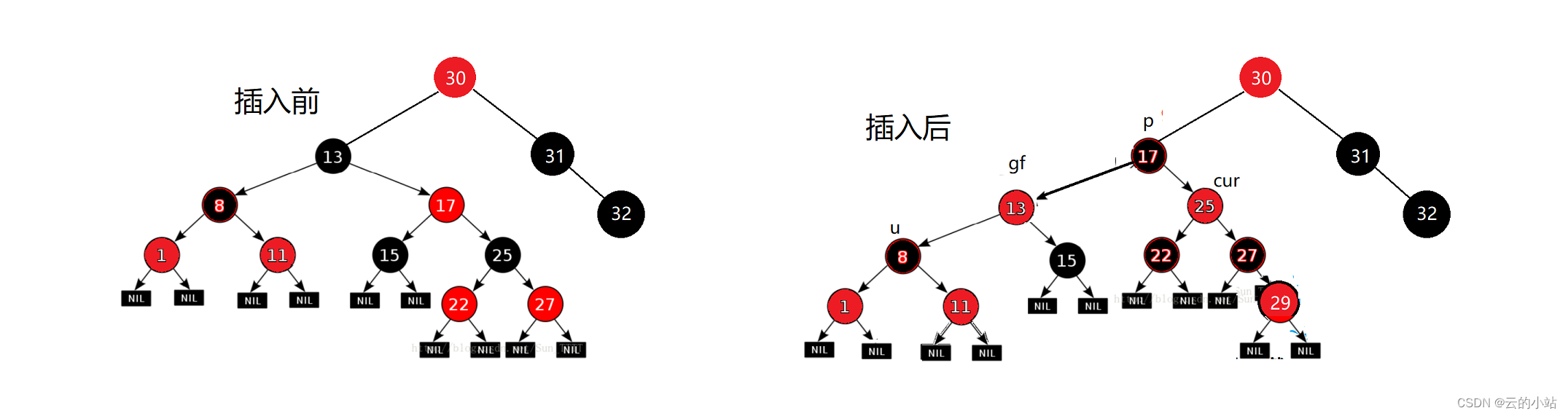
看上图，这样我们30的左子树插入一个结点后旋转，但是插入后路径的黑结点都是2未该改变，这样我们就30结点左子树的插入不会影响与右子树路径黑结点数量的差。30插入前后左右子树路径的黑色结点都是2个黑
将grandfather指针赋值给cur后，重新标定cur与parent位置，但注意不能随意标定grandfather，为什么呢？我们的parent可能为空。
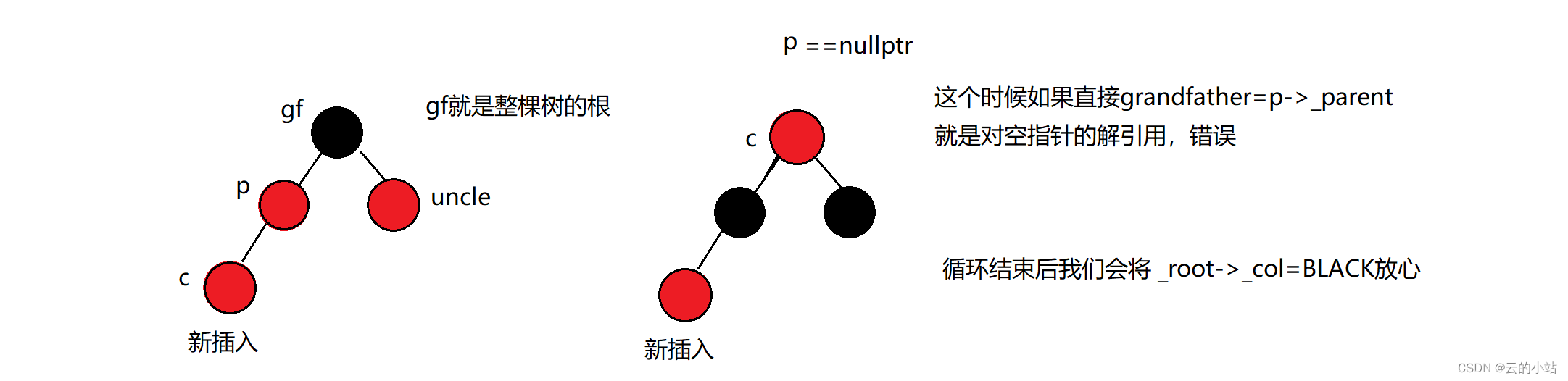
所以只有在parent存在且为红的时候我们才可以对grandfather赋值。
情况五：双旋情况
改吧改吧红黑树
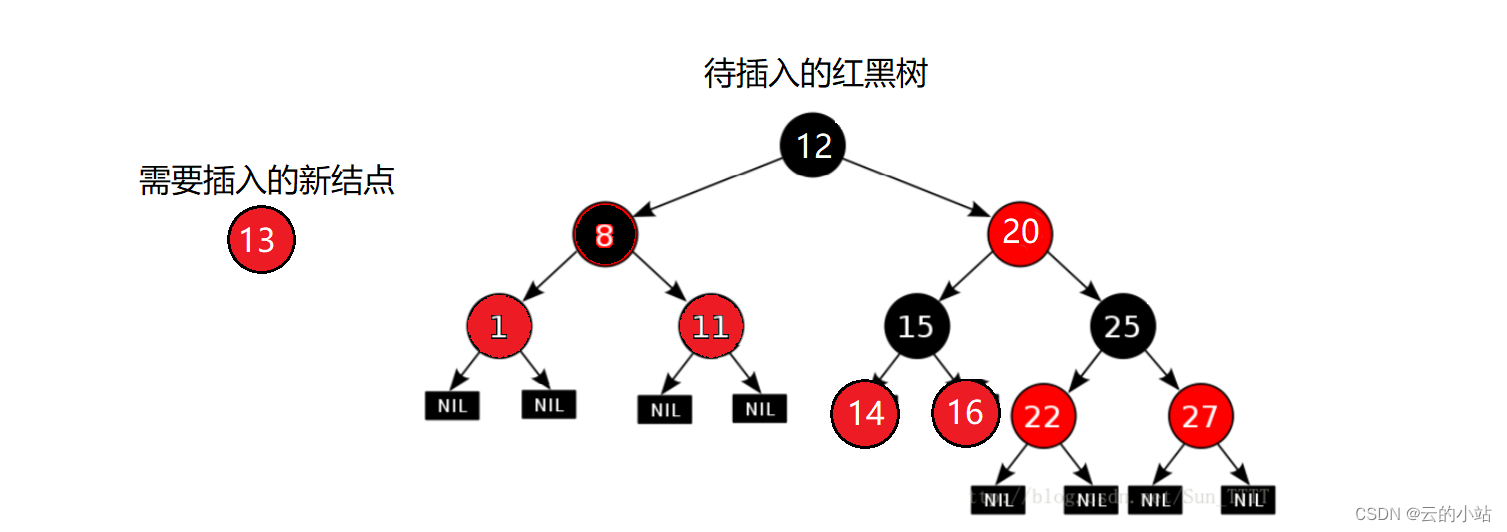
我们现在需要插入数据为13的结点，先链接到树中
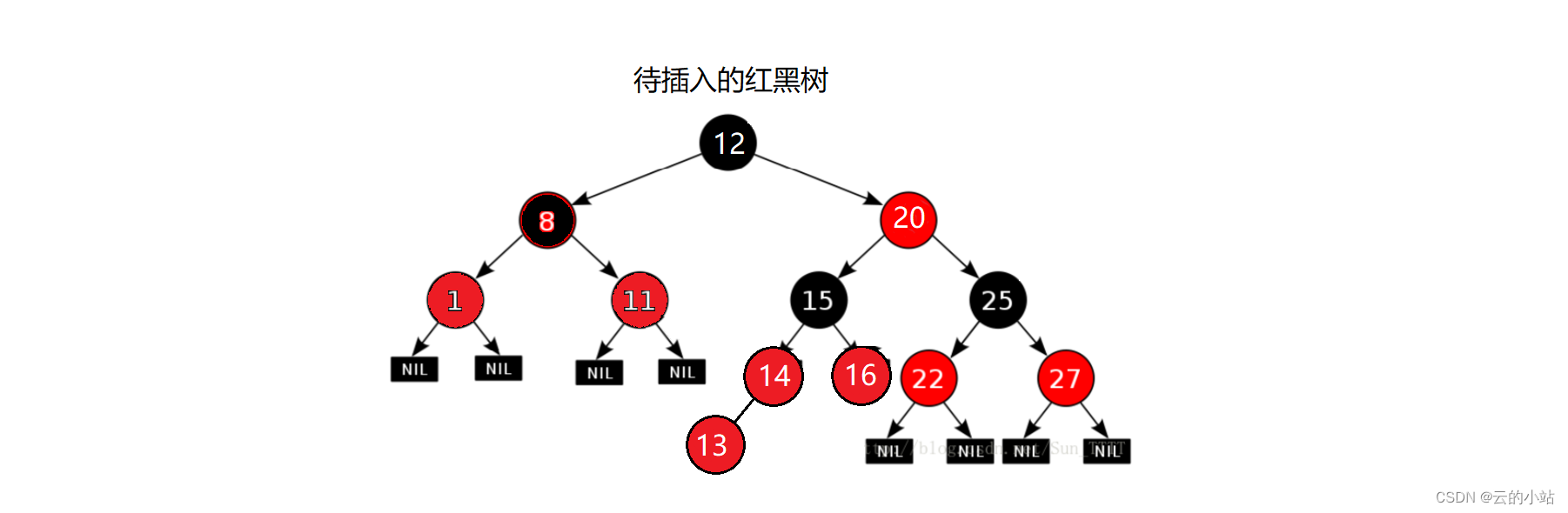
查看cur->parent是否为黑色或不存在，黑色停止，红色上色。
开始上色
uncle存在且为红
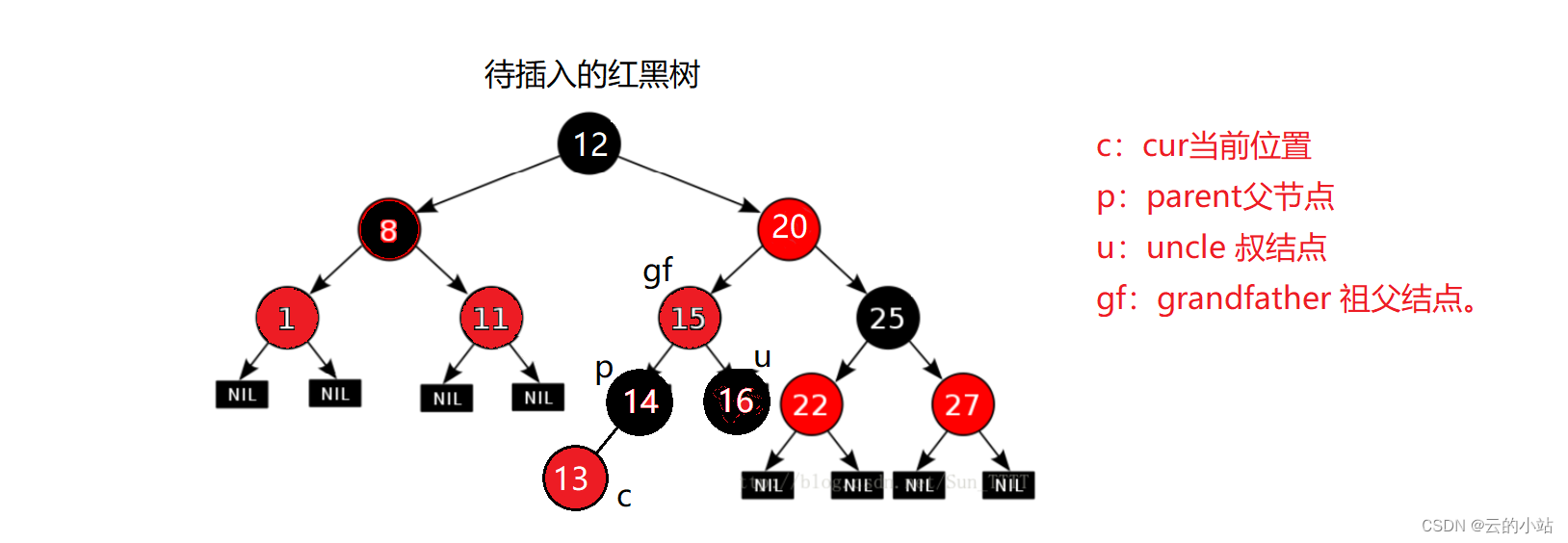
将grandfather指针赋值给cur，cur->parent._col==RED。继续循环，标定其他指针
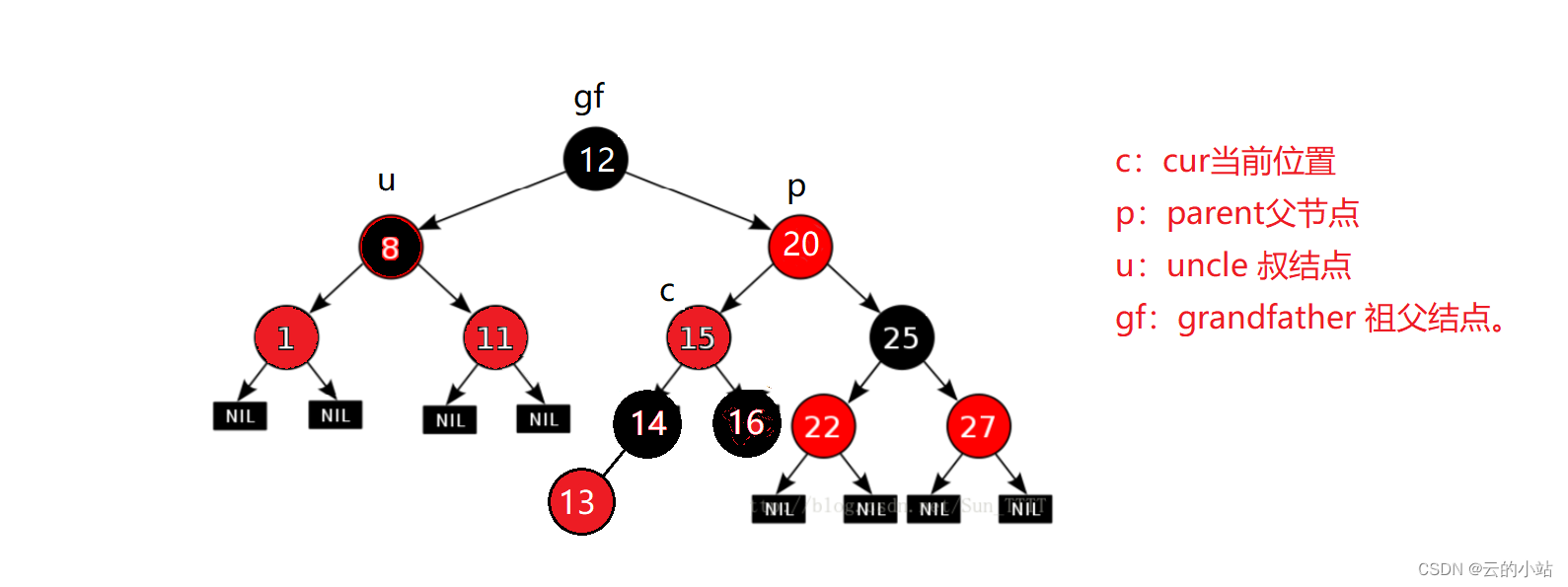
发现uncle这是为黑结点，我们需要开始旋转，发现gf->right==p p->left==cur所以我们这时候需要双旋存在，这棵树该先右旋在左旋
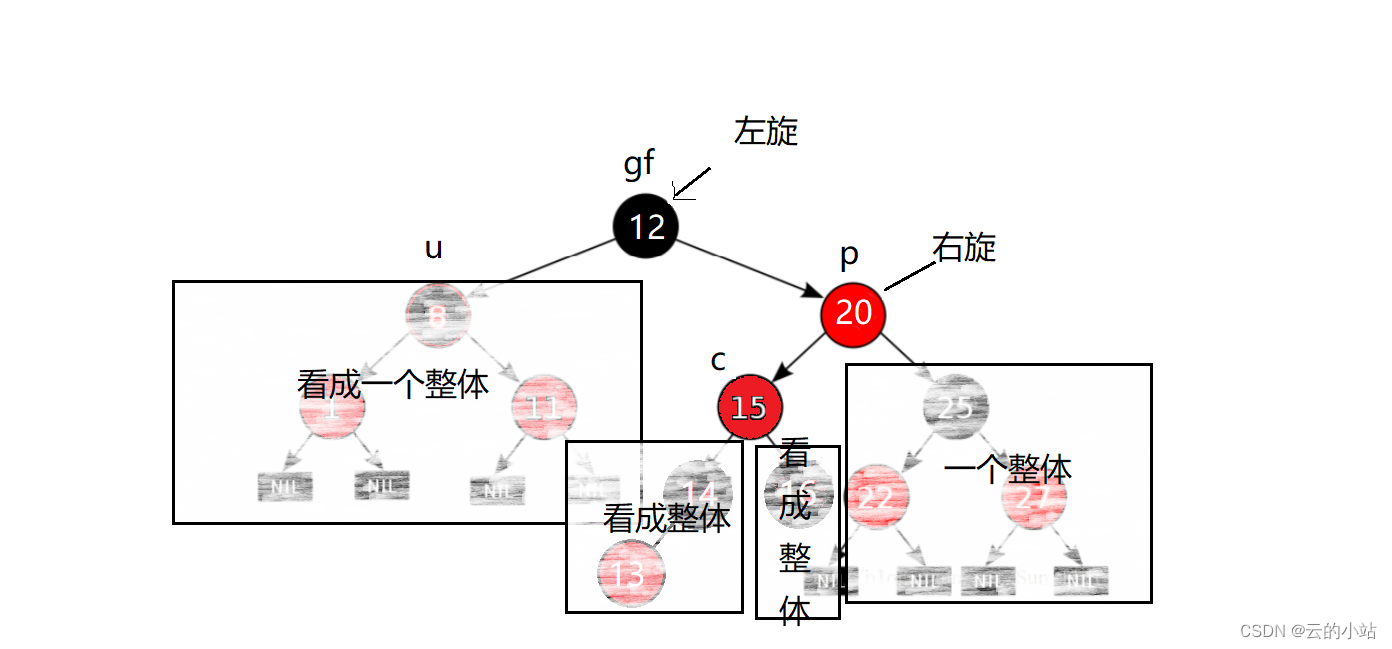变成概念图，好看多了吧~~
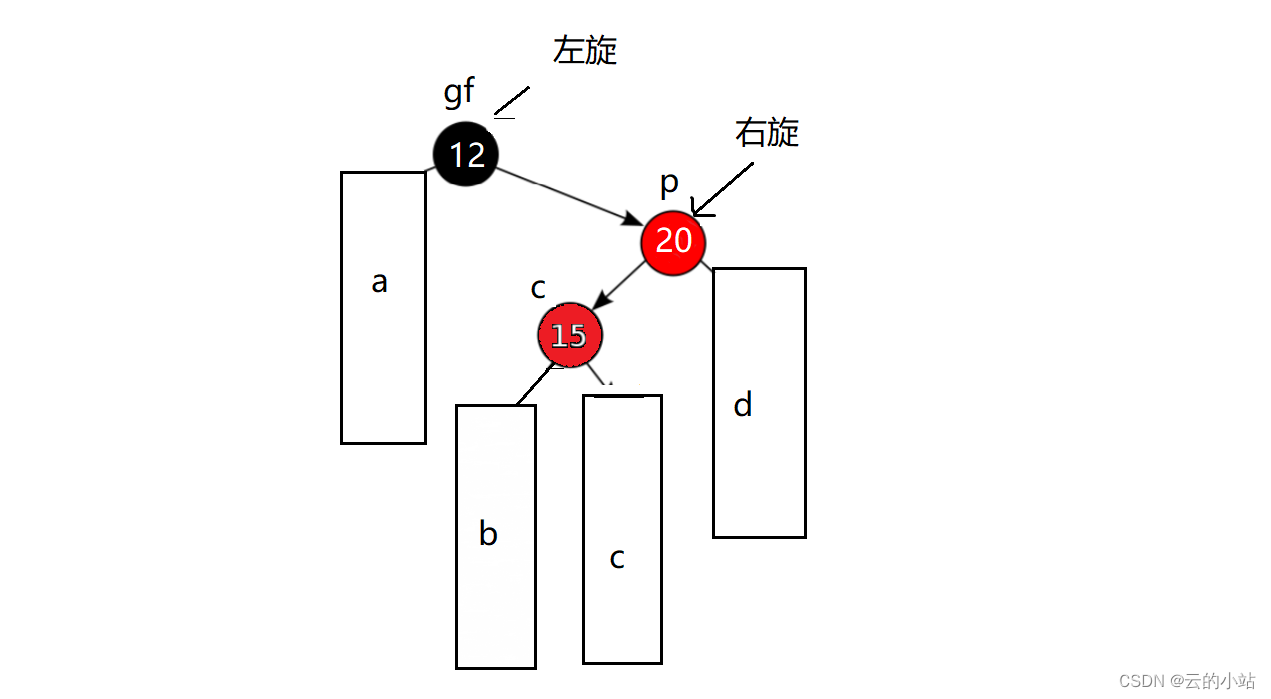
先对20结点右旋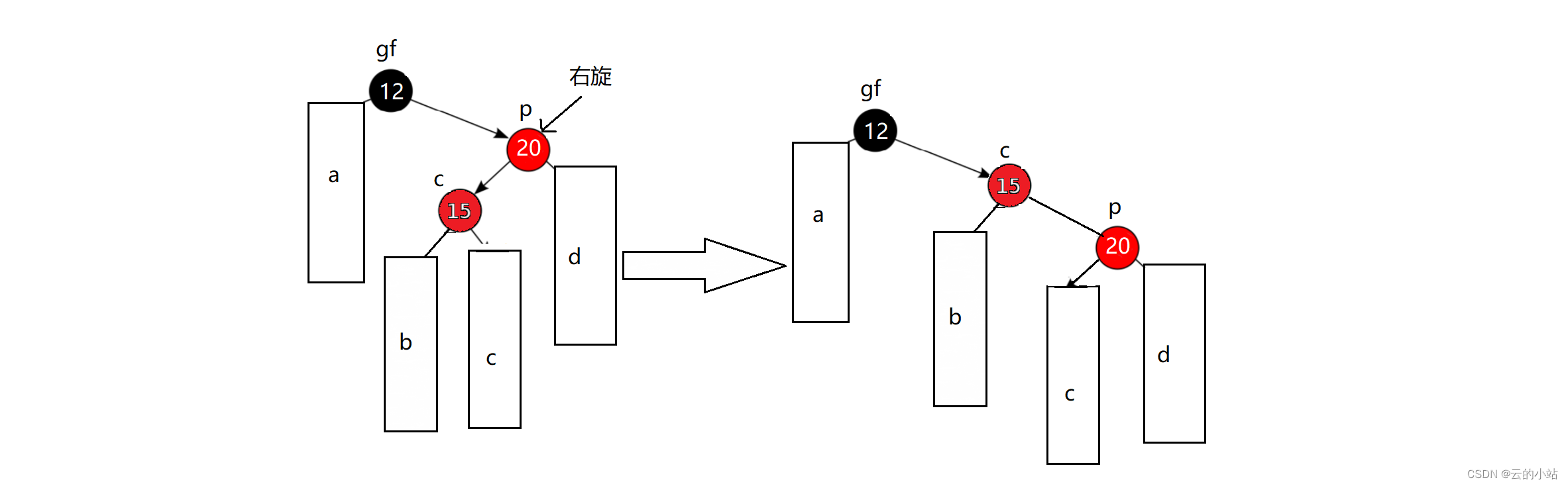
再对grandfather左旋
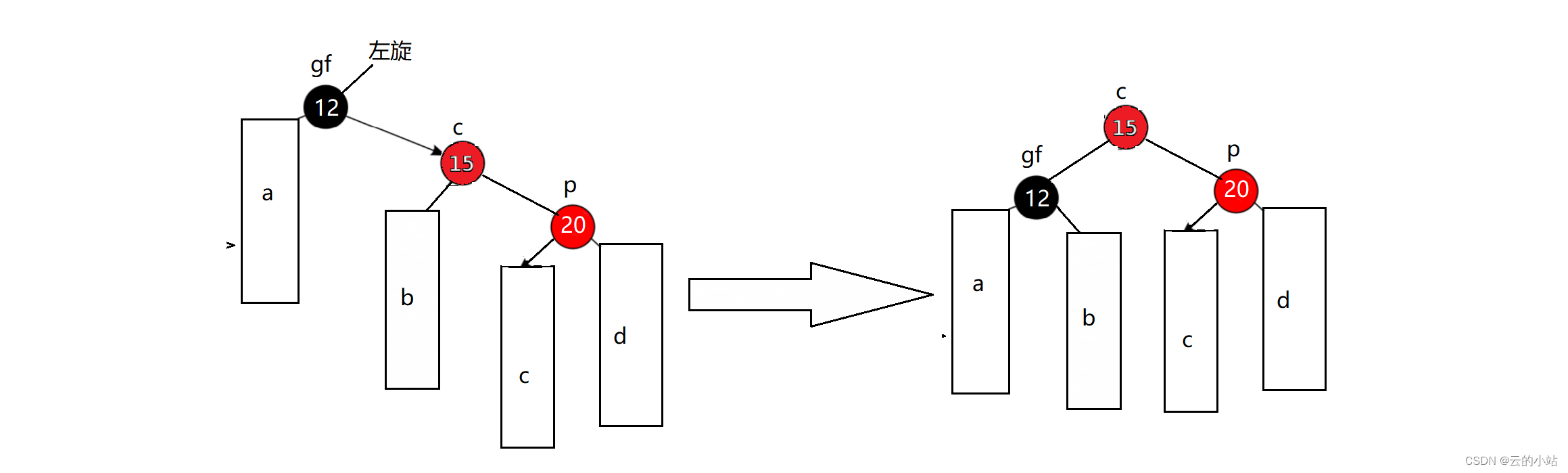
最后将cur颜色该为BLACK,grandfather改变为RED。
红黑树插入完整代码：
pair<iterator, bool> Insert(const T& data)
{
KeyOfT kot;
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
return make_pair(iterator(_root), true);
}
else
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
parent = cur;
if (kot(cur->_data) > kot(data))
{
cur = cur->_left;
}
else if (kot(cur->_data) < kot(data))
{
cur = cur->_right;
}
else
{
return make_pair(iterator(cur), false);
}
}
cur = new Node(data);
Node* ret = cur;
if (kot(parent->_data) < kot(cur->_data))
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
assert(grandfather->_col == BLACK);
Node* uncle = nullptr;
if (parent == grandfather->_left)
{
uncle = grandfather->_right;
//情况一：uncle存在，且为红。
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
//情况二+三：uncle不存在，或者存在为黑。
else
{
//单旋
if (parent->_left == cur)
{
RotateR(parent->_parent);
parent->_col = BLACK;
grandfather->_col = RED;
}
//双旋
else
{
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else /*if (parent == grandfather->_right)*/
{
uncle = grandfather->_left;
//情况一：uncle存在，且为红。
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
//情况二+三：uncle存在，且为红。
else
{
if (parent->_right == cur)
{
RotateL(parent->_parent);
parent->_col = BLACK;
grandfather->_col = RED;
}
//双旋
else
{
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
int n = 0;
}
break;
}
}
}
_root->_col = BLACK;
return make_pair(iterator(ret), true);
}
}
//......其他代码
public:
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
Node* pparent = parent->_parent;
parent->_parent = subR;
subR->_left = parent;
if (_root == parent)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (pparent->_left == parent)
{
pparent->_left = subR;
}
else
{
pparent->_right = subR;
}
subR->_parent = pparent;
}
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
Node* pparent = parent->_parent;
parent->_parent = subL;
subL->_right = parent;
if (_root == parent)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (pparent->_left == parent)
{
pparent->_left = subL;
}
else
{
pparent->_right = subL;
}
subL->_parent = pparent;
}
}
![强化学习从基础到进阶-常见问题和面试必知必答[3]：表格型方法：Sarsa、Qlearning；蒙特卡洛策略、时序差分等以及Qlearning项目实战](https://img-blog.csdnimg.cn/d553c7dadca54bdb82a3a234befb74d8.png#pic_center)
