0. 楔子
Diffusion Models(扩散模型)是在过去几年最受关注的生成模型。2020年后,几篇开创性论文就向世界展示了扩散模型的能力和强大:
- Diffusion Models Beat GANs on Image Synthesis(NeurIPS 2021 Spotlight, OpenAI团队, 该团队也是DALLE-2的作者)
[1]

Various images generated by DALL-E 2 (OpenAI)
[2].
- Latent Diffusion Models (LDM)(CVPR 2022, 现在在图文生成中广为使用的Stable Diffusion和MidJourney就是基于LDM开发的!)
基于LDM的Stable Diffusion基础模型的效果图 (Civitai.com)
[3].

MidJourney v5.1
[4]效果
震惊于Diffusion Models的成功浪潮,许多机器学习从业者都对其内部原理感兴趣。
虽然用Diffusion的理念来做生成模型最早出现在ICML2015的[6],Sohl-Dickstein使用了**非平衡热力学(Nonequilibrium Thermodynamics)**的理论来做。但是直到4年后,现就职于CalTech和OpenAI的Yang Song(Generative Modeling by Estimating Gradients of the Data Distribution, NeurIPS 2019)和Google Brain的Jonathan Ho的代表性论文出现(Denoising Diffusion Probabilistic Models (DDPM), NeurIPS 2020),才正式代表了Diffusion Models进入了大众视野。
有趣的是,两个人都是华人,说明华人在生成模型领域的开创性进展是世界级的,非常棒!
本文将基于Phil Wang对Jonathan Ho的DDPM的PyTorch实现[5](其代码是严格基于Tensorflow的原版实现而做的, 目前Github仓库已有4700+ stars)的代码结构,介绍训练和使用Diffusion Models的具体内容。
1. 什么是Diffusion Models?
首先, 在进行具体的技术性展开之前,需要回顾下Diffusion Model是什么:
如下图所示,可以简单将MidJourney, Stable Diffusion, ImageGen, DALLE-2这种Diffusion Model理解为从噪声中生成图像(generate images from noise) 的一种模型。

具体来说,Diffusion Models是生成模型的一种,这意味着Diffusion Models和GAN,VAE等生成模型范式一样:生成的数据和训练的数据类似(从概率论的角度上来说,就是生成模型的重点是模拟训练数据的分布)。
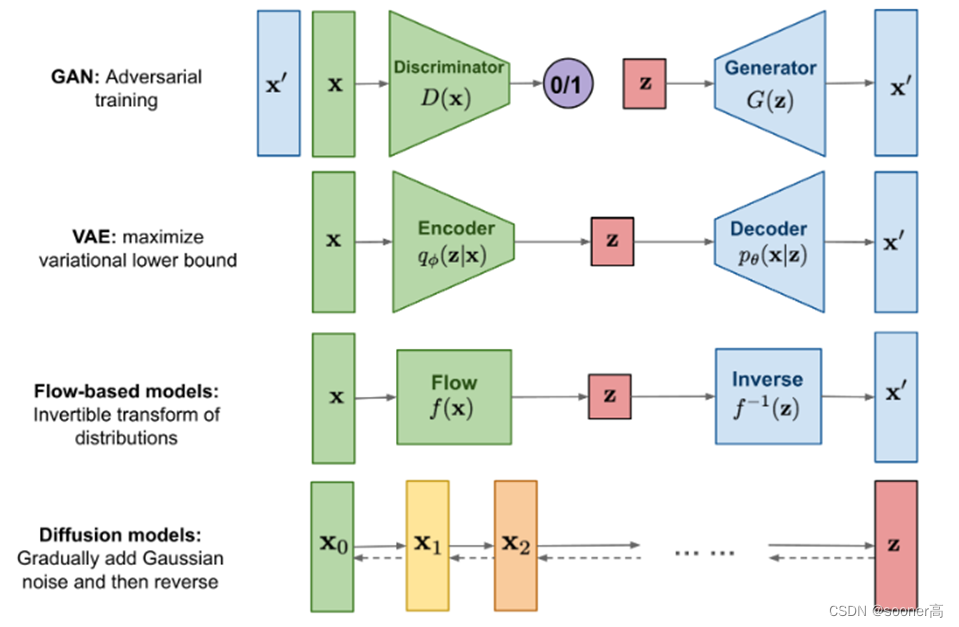
4类经典生成模型架构: GAN, VAE, Flow-based models和Diffusion models
从根本上说,扩散模型的工作原理是通过连续添加高斯噪声来破坏训练数据,然后通过反转这个噪声过程来学习恢复数据。
Diffusion Models work by destroying training data through the successive addition of Gaussian noise, and then learning to recover
the data by reversing this noising process
Diffusion models训练完成后,我们可以通过 学到的去噪过程传递(learned denoising process) 随机采样的噪声来生成数据。
更具体地说,Diffusion models是一个隐变量模型(latent variable model),它使用固定的Markov chain(马尔可夫链)将图像(Image)映射到隐空间(Latent space)。
这个过程是通过逐渐的对输入数据(图像)加噪声,来获得最优的后验
q
(
x
1
:
T
∣
x
0
)
q(\mathbf{x}_{1:T}|\mathbf{x}_0)
q(x1:T∣x0),这里
x
1
,
.
.
.
,
x
T
\mathbf{x}_{1}, ..., \mathbf{x}_{T}
x1,...,xT是和
x
0
\mathbf{x}_0
x0尺度一样的隐变量(latent variable),下图展示了这种加噪的过程:

最终,图像渐近变换为纯高斯噪声(pure Gaussian noise)。注意,我们训练扩散模型的目标,其实是学习反向过程:训练
p
θ
(
x
t
−
1
∣
x
t
)
p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t})
pθ(xt−1∣xt),通过沿着这条马尔可夫链向后遍历,我们可以从噪声中恢复原始的图像:

2. Diffusion Models的优点
如上所述,近年来对扩散模型的研究呈爆炸式增长。受非平衡热力学[1]的启发,扩散模型目前可以产生最先进的图像质量,并且解决了GAN生成数据范围受限的问题(一个GAN模型通过只能用来一类数据,比如人脸,服装,室内场景等,而1个Diffusion Models就可以完全生成各种各样的数据!)
除了很高的图像质量,Diffusion Models还具有许多其他优点:
- 不需要对抗性训练(❌ adversarial training): GAN中的对抗性训练的困难是非常明显的,通常会导致Model collapse, 训练出一个良好的GAN通常会消耗很多时间在调试上;
- 训练效率方面高(✔ training efficiency): 扩散模型还具有可扩展性和并行性的额外好处, 因为其网络结构简单和训练规则清晰的原因,多机多卡的并行难度相比GAN来说低很多(GAN可能有很多级联的Generator和Discriminator,所以在设计并行训练时候通常需要进行一些复杂的手动切分模型操作)。
虽然扩散模型似乎是凭空产生的结果,但有许多仔细而有趣的数学选择和细节为这些结果提供了基础,并且最佳实践仍在文献中不断发展。结合DDPM,我们需要更加深入的理解一下扩散模型背后的数学理论和逻辑。
3. 更多的数学
第1部分我们提到了Diffusion Model的目标: 训练 p θ ( x t − 1 ∣ x t ) p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_{t}) pθ(xt−1∣xt),通过沿着这条马尔可夫链向后遍历,我们可以从噪声中恢复原始的图像。
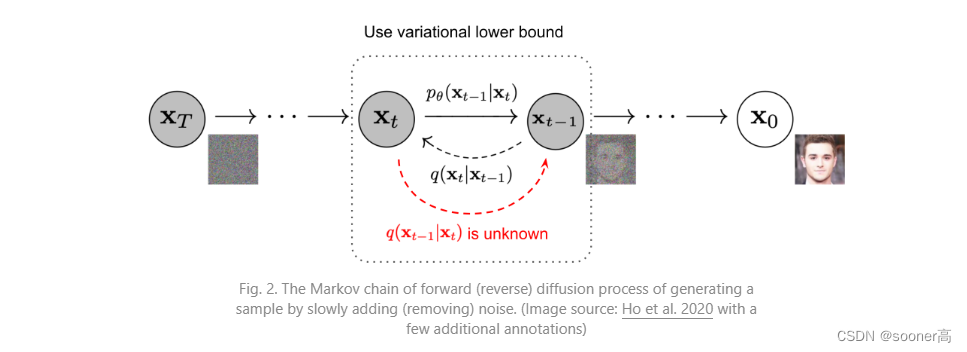
现在,我们需要一个数学上更正式的表达,因为最终需要一个可处理的损失函数,我们的神经网络需要优化它。
如上图(来自DDPM论文)所示,我们用 q ( x 0 ) q(\mathbf{x_0}) q(x0)表示真实的训练数据分布(real images),我们可以从这个分布中任意采样得到图像: x 0 ∼ q ( x 0 ) \mathbf{x_0} \sim q(\mathbf{x_0}) x0∼q(x0)。
3.1 Forward Pass 前向过程
q
(
x
t
∣
x
t
−
1
)
q(\mathbf{x}_t|\mathbf{x}_{t-1})
q(xt∣xt−1)
我们将前向过程(Forward pass, 在每个timestep上加Gaussian noise) q ( x t ∣ x t − 1 ) q(\mathbf{x}_t|\mathbf{x}_{t-1}) q(xt∣xt−1), 根据已知的方差表 0 < β 1 < β 2 < . . . < β T < 1 0 < \beta_1 < \beta_2 < ... < \beta_T < 1 0<β1<β2<...<βT<1,定义为:
q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) q(\mathbf{x}_t|\mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1-\beta_t}\mathbf{x}_{t-1}, \beta_t\mathbf{I}) q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)
我们知道,标准正态分布( N \mathcal{N} N)由2个参数定义:
- 均值 μ \mu μ
- 标准差 σ 2 ≥ 0 \sigma^2 \ge0 σ2≥0
那么基本上,在时间步(timestep) t t t上的新图像(slightly noisier new image)是从一个条件高斯分布(conditional Gaussian distribution) 中绘制的,其中 μ t = 1 − β t x t − 1 , σ 2 = β t \mu_{t} = \sqrt{1-\beta_t}\mathbf{x}_{t-1}, \sigma^2=\beta_t μt=1−βtxt−1,σ2=βt。
那这种情况下,时间步(timestep) t t t上的新图像的生成过程,就可以转化为从标准正态分布中取的一个噪声 : ϵ ∼ N ( 0 , I ) \epsilon \sim \mathcal{N}(0, \mathbf{I}) ϵ∼N(0,I),并让 x t = 1 − β t x t − 1 + β t ϵ \mathbf{x}_t =\sqrt{1-\beta_t}\mathbf{x}_{t-1}+\sqrt{\beta_t}\epsilon xt=1−βtxt−1+βtϵ
这里, β t \beta_t βt在每个timestep的值并不相同,事实上, β t \beta_t βt随timestep变化的过程可以理解为variance schedule,其变化可以是linear, quadratic, cosine的形式,类似于 学习率(learning rate) 的变化。
我理解这个
β
t
\beta_t
βt(either learned or fixed)的变化是研究人员根据任务收敛情况等内容设置的,此外,如果表现良好,当
T
T
T足够大的时候,
β
\beta
β的目标还是让Forward Pass中最后的
x
T
\mathbf{x}_T
xT变成一个pure/isotropic Gausssian noise[7]。
3.2 Backward Pass 后向过程
p
θ
(
x
t
−
1
∣
x
t
)
p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t)
pθ(xt−1∣xt)
刚刚Forward Pass解释完了,如果我们知道条件分布(conditional distribution) p ( x t − 1 ∣ x t ) p(\mathbf{x}_{t-1}|\mathbf{x}_{t}) p(xt−1∣xt), 我们就可以进行Backward Process了:
即采样一些随机的Gaussian noise x T \mathbf{x}_T xT,
并逐渐的denoise它们,最终得到和真实数据分布一致的数据 x 0 \mathbf{x}_0 x0
但是,这个条件概率我们其实是不知道的,它很难处理(intractable),因为它需要知道所有可能图像的分布,以便计算这个条件概率。因此,我们想要利用神经网络的能力去approximate (learn) 这个条件概率 (conditional probability distribution)。
具体的,我们想要学习的条件概率的数学表达为 p θ ( x t − 1 ∣ x t ) p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t) pθ(xt−1∣xt), 其中 θ \theta θ代表了神经网络的参数,通过梯度进行优化。
Ok, 所以不同于Forward Pass中直接的解析解一样的加噪过程,我们在Backward Pass中需要一个神经网络来表示这个条件概率分布。如果我们假定这个反向过程也是Gaussian的,回忆下,任意的Gaussian distribution是由 均值 μ θ \mu_{\theta} μθ和方差 ∑ θ \sum_\theta ∑θ 定义的。
所以我们将这个过程类比Forward Pass,进行如下表示:
p
θ
(
x
t
−
1
∣
x
t
)
=
N
(
x
t
−
1
;
μ
θ
(
x
t
,
t
)
,
∑
θ
(
x
t
,
t
)
)
p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1};\mu_{\theta(\mathbf{x}_t, t)}, \sum_{\theta}(\mathbf{x}_t, t))
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),θ∑(xt,t))
这里均值和方差都受到 t t t(timestep,也称为noise level)的控制。
到这里,我们的神经网络需要学习/表示的内容其实就是均值和方差。然而, DDPM的作者Jonathan Ho决定想要保证方差固定,让神经网络只学习这个条件概率分布的均值 μ θ \mu_{\theta} μθ:
根据论文所述,我们将上面的式子变成如下形式
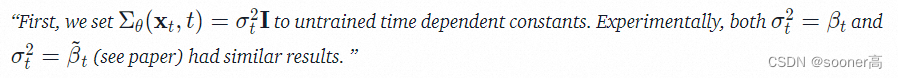
p
θ
(
x
t
−
1
∣
x
t
)
=
N
(
x
t
−
1
;
μ
θ
(
x
t
,
t
)
,
σ
t
2
I
)
p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1};\mu_{\theta(\mathbf{x}_t, t)}, \sigma^2_{t}\mathbf{I})
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),σt2I)
后续的论文进一步优化了DDPM,让神经网络同时优化均值 μ θ \mu_{\theta} μθ和方差 ∑ θ \sum_{\theta} ∑θ。
这里我们不展开后续的工作,我们的目标是基于DDPM的代码结构和论文,彻底理解一个Diffusion Model的训练,推理中的所有关键环节,所以我们继续,假设我们的神经网络只需要学习/表示这个条件概率分布的均值 μ θ \mu_{\theta} μθ。
4. 定义DDPM的目标/损失函数(对均值
μ
θ
\mu_{\theta}
μθ进行reparametrization)
为了获得Backward Pass中,均值
μ
θ
\mu_{\theta}
μθ的objective function(目标函数),Jonathon Ho等人观察到,
q
(
x
t
∣
x
t
−
1
)
q(\mathbf{x}_t|\mathbf{x}_{t-1})
q(xt∣xt−1)(Forward Pass)和
p
θ
(
x
t
−
1
∣
x
t
)
p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t)
pθ(xt−1∣xt)(Backward Pass)的组合可以视为一种VAE(Variational AutoEncoder)[8]。因此,根据VAE的概念,其变分下边界(variational lower bound, 也称为ELBO)[9]可以用于最小化相对于真实数据样本
x
0
\mathbf{x}_0
x0的负对数似然(negative log-likelihood)。
关于VAE和其下界ELBO(Evidence Lower BOund)的推导过程这里不展开,这里只把定义拿过来,供忘记了的朋友有个印象:
在这里,VAE的下界ELBO其实是每个timestep t t t时的损失函数之和: L = L 0 + L 1 + . . . + L T L=L_{0} + L_{1} + ... + L_{T} L=L0+L1+...+LT。通过Forward Pass q ( x t ∣ x t − 1 ) q(\mathbf{x}_t|\mathbf{x}_{t-1}) q(xt∣xt−1)和Backward Pass p θ ( x t − 1 ∣ x t ) p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t) pθ(xt−1∣xt)的构建,损失函数 L L L的每一项, 除 L 0 L_0 L0以外,实际上就是2个Gaussian distributions的KL divergence (KL散度,用于衡量分布之间的相似性)。
在实现中,这个KL divergence实际上可以显式的写为关于均值 μ \mu μ的L2 Loss!后面会详细讲代码的时候会提到。
像2015年ICML的论文Deep Unsupervised Learning using Nonequilibrium Thermodynamics[6]展示的那样,Forward Pass
q
(
x
t
∣
x
t
−
1
)
q(\mathbf{x}_t|\mathbf{x}_{t-1})
q(xt∣xt−1)构建的直接结果是我们可以在任意噪声水平(arbitrary noise level)下采样出
x
t
\mathbf{x}_t
xt(基于
x
0
\mathbf{x}_0
x0,因为高斯分布的和还是高斯分布, sums of Gaussians is also Gaussian)。这个思路很方便,这意味着我们可以直接从
x
0
\mathbf{x}_0
x0得到某个timestep
t
t
t时的
x
t
\mathbf{x}_t
xt, 而非迭代式的、线性的从
x
0
,
x
1
,
.
.
.
,
x
t
\mathbf{x}_0, \mathbf{x}_1, ..., \mathbf{x}_t
x0,x1,...,xt一步步的从
0
0
0走到
t
t
t,这种直接从
x
0
\mathbf{x}_0
x0到
x
t
\mathbf{x}_t
xt的方式用数学表达为如下形式:
q ( x t ∣ x 0 ) = N ( x t ; α t ‾ x 0 , ( 1 − α t ‾ ) I ) ) q(\mathbf{x}_t | \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\overline{\alpha_t}}\mathbf{x}_0, (1-\overline{\alpha_t})\mathbf{I})) q(xt∣x0)=N(xt;αtx0,(1−αt)I))
这里,
q
(
x
t
∣
x
0
)
q(\mathbf{x}_t | \mathbf{x}_0)
q(xt∣x0)的推导过程如下:
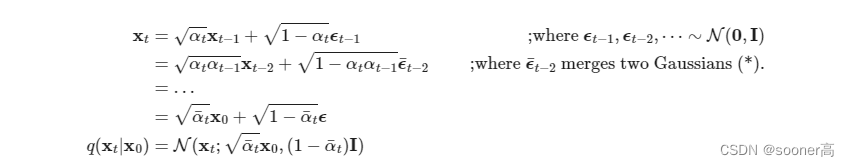
其中, α t : = 1 − β t , α t ‾ : = ∏ s = 1 t α s \alpha_t := 1 - \beta_t, \overline{\alpha_t} := \prod_{s=1}^{t}\alpha_s αt:=1−βt,αt:=∏s=1tαs, 我们把这个方程称为 “优雅的性质”(Nice property),这意味着我们可以对Gaussian noise进行采样并适当缩放, 从而可以直接地从 x 0 \mathbf{x}_0 x0得到 x t \mathbf{x}_t xt。
这里需要注意的是, α t ‾ \overline{\alpha_t} αt是已知的variance schedula β t \beta_t βt的函数,因此其是可以 预计算(precomputed) 的。这使得我们在训练过程中,可以随机的采样timestep t t t,并优化对应的损失函数 L t L_t Lt。
此外,如DDPM论文提到的那样(其中的数学解释的部分请参考What are Diffusion Models?这篇博客),其另一个优雅的性质是重新参数化平均值,使神经网络 ϵ θ ( x t , t ) \epsilon_{\theta}(\mathbf{x}_t, t) ϵθ(xt,t)学习(预测)添加的噪声(Reparametrize the mean to make the neural network learn/predict the added noise (via a network ϵ θ ( x t , t ) \epsilon_{\theta}(\mathbf{x}_t, t) ϵθ(xt,t) for noise level t t t)), 而这个添加的噪声就是loss function的KL term中的一项。
这里补充一下KL term,或者KL
divergence的概念,其本质上就是衡量概率分布 P P P和概率分布 Q Q Q的距离的熵,是由Kullback和Leibler提出的一种相对熵的概念。
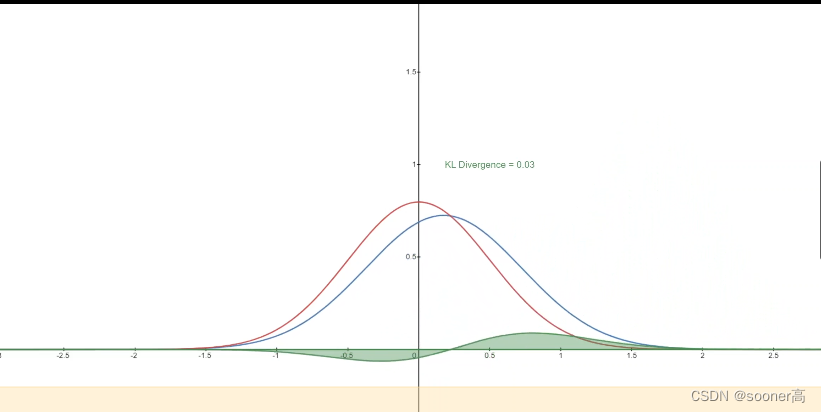
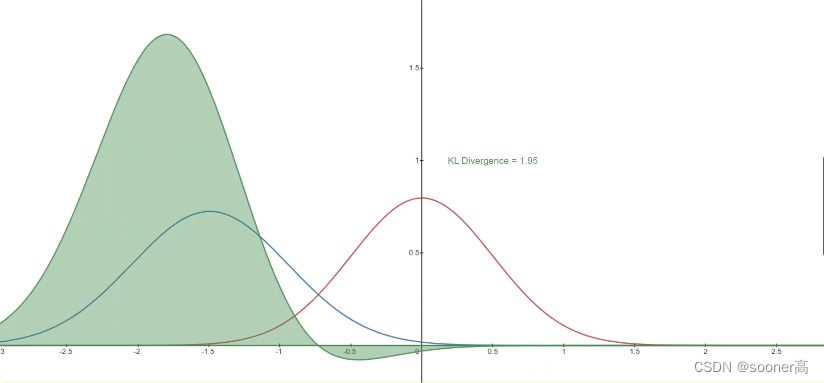
下图展示的是变化的分布P (blue) 和标准的正态部分Q (red)的KL 散度,绿色曲线表示上述KL散度定义中积分内的函数,可以看出,当P和Q越接近,KL Divergence的值就越小,反之则越来越大。
这意味着我们的神经网络变成了一个noise predictor(噪声预测器),而不是一个直接的mean predictor(均值预测器)。
均值可以按如下方式进行计算:
μ θ ( x t , t ) = 1 α t ( x t − β t 1 − α t ‾ ϵ θ ( x t , t ) ) \mu_{\theta}(\mathbf{x}_t, t) = \frac{1}{\sqrt{\alpha_t}} (\mathbf{x}_t - \frac{\beta_t}{\sqrt{1-\overline{\alpha_t}}}\epsilon_{\theta}(\mathbf{x}_t, t)) μθ(xt,t)=αt1(xt−1−αtβtϵθ(xt,t))
其推导过程如下
4.1 μ θ ( x t , t ) \mu_{\theta}(\mathbf{x}_t, t) μθ(xt,t)的推导过程
回顾Backward Pass中的目标, 用
p
θ
(
x
t
−
1
∣
x
t
)
=
N
(
x
t
−
1
;
μ
θ
(
x
t
,
t
)
,
σ
t
2
I
)
p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1};\mu_{\theta(\mathbf{x}_t, t)}, \sigma^2_{t}\mathbf{I})
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),σt2I)来替代
q
(
x
t
−
1
∣
x
t
)
q(\mathbf{x}_{t-1}|\mathbf{x}_{t})
q(xt−1∣xt),
这是由于
q
(
x
t
−
1
∣
x
t
)
q(\mathbf{x}_{t-1}|\mathbf{x}_{t})
q(xt−1∣xt)的数据集很难用1个给定的先验数据分布来唯一确定,所以需要用一个神经网络
p
θ
p_{\theta}
pθ来学习
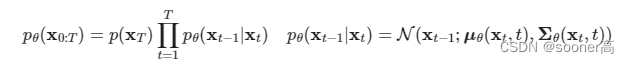
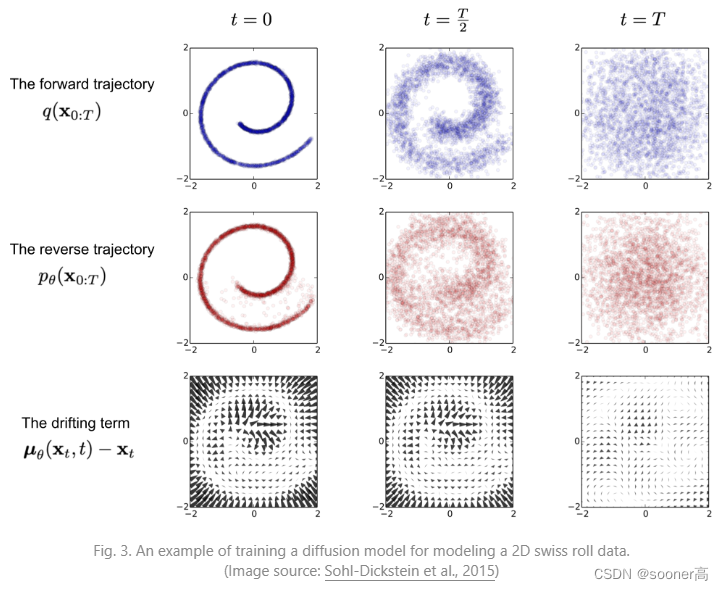
从Forward Pass的定义来看,虽然在逆向过程(reverse conditional probability)(
x
T
\mathbf{x}_T
xT到
x
0
\mathbf{x}_0
x0) 比较困难,但是当给定
x
0
\mathbf{x}_0
x0的时候,即当有
q
(
x
t
−
1
∣
x
t
,
x
0
)
q(\mathbf{x}_{t-1}|\mathbf{x}_{t},\mathbf{x}_{0})
q(xt−1∣xt,x0)的时候(先验多了真实数据
x
0
\mathbf{x}_0
x0), 此逆向过程可解:

4.2 目标/损失函数
由4.1可知,DDPM要优化的均值 μ \mu μ,经过了重参数化操作,变成了预测添加的噪声 ϵ t \epsilon_t ϵt,最终,我们要优化的损失函数 L t L_t Lt的表示如下:
∣ ∣ ϵ − ϵ θ ( x t , t ) ∣ ∣ 2 = ∣ ∣ ϵ − ϵ θ ( α t ‾ x 0 + ( 1 − α t ‾ ) ϵ , t ) ∣ ∣ 2 ||\epsilon - \epsilon_{\theta}(\mathbf{x}_t, t) ||^2 = || \epsilon - \epsilon_{\theta}(\sqrt{\overline{\alpha_t}}\mathbf{x}_0 + \sqrt{(1-\overline{\alpha_t})}\epsilon, t) ||^2 ∣∣ϵ−ϵθ(xt,t)∣∣2=∣∣ϵ−ϵθ(αtx0+(1−αt)ϵ,t)∣∣2
这里 x 0 \mathbf{x}_{0} x0是原始的训练图片, x t \mathbf{x}_{t} xt是有固定的Forward pass在noise level t t t得到的加噪结果。 ϵ \epsilon ϵ是在timestep t t t采样得到的pure noise, ϵ θ ( x t , t ) \epsilon_{\theta}(\mathbf{x}_t, t) ϵθ(xt,t)则是我们的神经网络,其用一个简单的MSE Loss来优化真实的Gaussian noise和预测的Gaussian noise。
训练代码解释如下(最通俗解释):
- ① 从训练集随机采样一个原始数据 x 0 \mathbf{x}_{0} x0
- ② 从 0 到 T 0 到 T 0到T中间,随机选取一个timestep t t t, 可以直接通过 q ( x t ∣ x 0 ) q(\mathbf{x}_t | \mathbf{x}_0) q(xt∣x0)获得 x t \mathbf{x}_t xt, x t \mathbf{x}_t xt即为对原始数据 x 0 \mathbf{x}_{0} x0的加噪的结构(或者说是corrupted result)
- ③ 随机从 N ( 0 , I ) \mathcal{N}(0, \mathbf{I}) N(0,I)采样得到噪声 ϵ \epsilon ϵ
- ④ 将 timestep
t
t
t, 系数
α
t
‾
:
=
∏
s
=
1
t
α
s
\overline{\alpha_t} := \prod_{s=1}^{t}\alpha_s
αt:=∏s=1tαs, 图片数据
x
0
\mathbf{x}_{0}
x0和 Gaussian noise
ϵ
\epsilon
ϵ输入到神经网络
ϵ
θ
\epsilon_{\theta}
ϵθ中,得到预测值,然后让其和真实的采样得到的噪声
ϵ
\epsilon
ϵ进行MSE Loss,用来优化神经网络
ϵ
θ
\epsilon_{\theta}
ϵθ

在实际的代码中,训练是按batch进行的,目前最流行的优化器是AdamW。
5. 神经网络
显然,由上面的目标函数和神经网络的要求可以看出,对神经网络
ϵ
θ
\epsilon_{\theta}
ϵθ唯一的要求是输入输出的维度一致。
很明显,Autoencoder架构很适合做这样的事情,Autoencoder在Encoder和Decoder之间有一个所谓的“Bottleneck”层。Encoder首先将图像编码成一个维度较小的Hidden Representation,称为“Bottleneck”,然后Decoder再将该Hidden Representation表示解码回实际图像。这迫使网络只在Bottleneck层保留最重要的信息。
在DDPM的实现中,其使用的是非常经典的U-Net网络[10]来制作这种Autoencoder的架构,这是最先进的图像分割模型架构,由德国弗赖堡大学发明,在图像的生成领域得到广泛使用,大名鼎鼎的StyleGAN2也采用了类似的结构。
U-Net同任何的像Autoencoder一样,由中间的Bottleneck层来确保网络只学习最重要的信息。重要的是,它引入了编码器和解码器之间的残差连接(residual connection),极大地改善了梯度的传递(Kaiming He的ResNet),加强了网络收敛的能力。
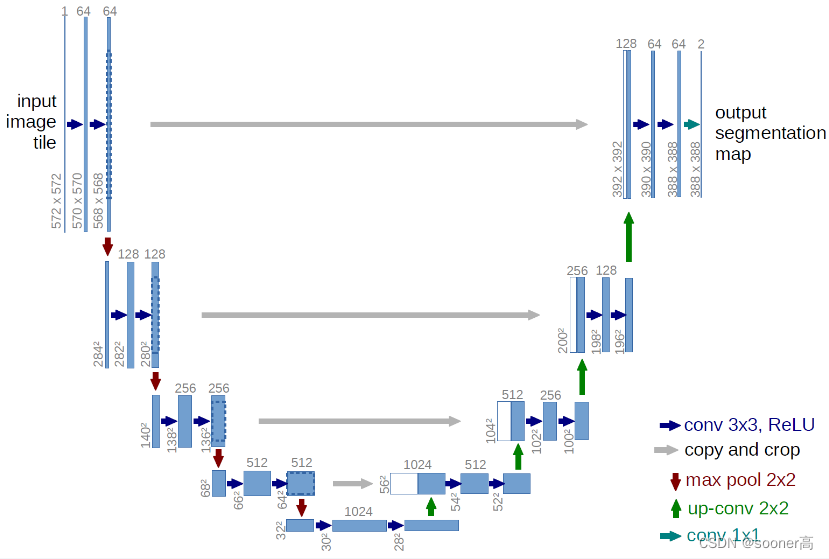
这里展示的是最经典的基础版U-Net,可以看出,经典U-Net模型首先对输入进行下采样,然后进行上采样,后续很多的U-Net升级版会增加更多的残差连接,然后制作不同层级的连接和模块的独特设计,不过本质没有什么变化。
在DDPM的实现中,其U-Net的结构如下所示:
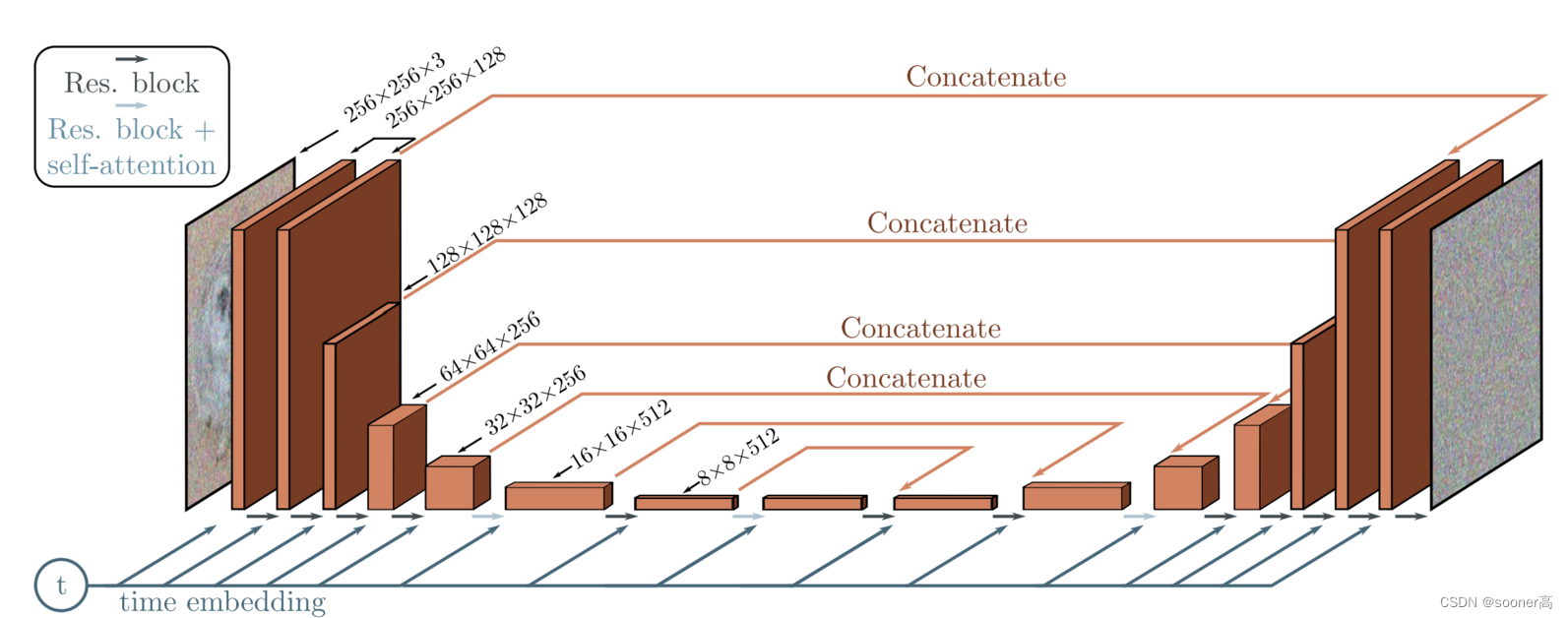
其网络层主要包含5块:
- Encoder blocks (不同于直接的卷积下采样,DDPM的Encoder模块使用了残差连接)
- Bottleneck blocks
- Decoder blocks (同样使用了残差连接)
- Self attention modules (DDPM在卷积之间加入了注意力模块,其注意力模块使用的是2个: 1是标准的Transformer的 multi-head self-attention
Attention,另一个是线性的linear attention variantLinearAttention,目的是减少计算量,其差别如下所示)
class Attention(nn.Module):
def __init__(self, dim, heads=4, dim_head=32):
super().__init__()
self.scale = dim_head**-0.5
self.heads = heads
hidden_dim = dim_head * heads
self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)
self.to_out = nn.Conv2d(hidden_dim, dim, 1)
def forward(self, x):
b, c, h, w = x.shape
qkv = self.to_qkv(x).chunk(3, dim=1)
q, k, v = map(
lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv
)
q = q * self.scale
sim = einsum("b h d i, b h d j -> b h i j", q, k)
sim = sim - sim.amax(dim=-1, keepdim=True).detach()
attn = sim.softmax(dim=-1)
out = einsum("b h i j, b h d j -> b h i d", attn, v)
out = rearrange(out, "b h (x y) d -> b (h d) x y", x=h, y=w)
return self.to_out(out)
class LinearAttention(nn.Module):
def __init__(self, dim, heads=4, dim_head=32):
super().__init__()
self.scale = dim_head**-0.5
self.heads = heads
hidden_dim = dim_head * heads
self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)
self.to_out = nn.Sequential(nn.Conv2d(hidden_dim, dim, 1),
nn.GroupNorm(1, dim))
def forward(self, x):
b, c, h, w = x.shape
qkv = self.to_qkv(x).chunk(3, dim=1)
q, k, v = map(
lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv
)
q = q.softmax(dim=-2)
k = k.softmax(dim=-1)
q = q * self.scale
context = torch.einsum("b h d n, b h e n -> b h d e", k, v)
out = torch.einsum("b h d e, b h d n -> b h e n", context, q)
out = rearrange(out, "b h c (x y) -> b (h c) x y", h=self.heads, x=h, y=w)
return self.to_out(out)
- Sinusoidal time embeddings (timestep embedding 的目的是告知模型,输入对应的noise level t t t, 也可理解成输入在Markov chain中的位置, 和NeRF中的positional encoding的意义差不多。)
本文主要的目标是关注整体的DDPM流程,因此没有贴出DDPM的整体U-Net的结构代码,如有需要,请查看denoising_diffusion_pytorch/guided_diffusion.py,这里不展开。
6. 前向&反向流程的实现和优化
6.1 前向过程定义(Defining the forward diffusion process)
前向过程的目标是逐渐的对原始图像加噪声,使其最终变成一个Gaussian Distribution。加噪的实现同时是需要
β
\beta
β的策略,原始版本的DDPM使用的是Linear schedule (不过目前,截止2023年,主流的加噪策略变成了cosine schedule,这里不详细展开,有兴趣的请看OpenAI发表于2021年的论文Improved Denoising Diffusion Probabilistic Models[11]):
如代码所示,我们把经典的Linear linear_beta_schedule和Cosine cosine_beta_schedule实现展示出来,这个的原则对于收敛还是有一定的影响的:
def linear_beta_schedule(timesteps):
"""
linear schedule, proposed in original ddpm paper
"""
scale = 1000 / timesteps
beta_start = scale * 0.0001
beta_end = scale * 0.02
return torch.linspace(beta_start, beta_end, timesteps, dtype = torch.float64)
def cosine_beta_schedule(timesteps, s = 0.008):
"""
cosine schedule
as proposed in https://openreview.net/forum?id=-NEXDKk8gZ
"""
steps = timesteps + 1
t = torch.linspace(0, timesteps, steps, dtype = torch.float64) / timesteps
alphas_cumprod = torch.cos((t + s) / (1 + s) * math.pi * 0.5) ** 2
alphas_cumprod = alphas_cumprod / alphas_cumprod[0]
betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1])
return torch.clip(betas, 0, 0.999)
以timestep T = 300 T=300 T=300为例,回顾一下优化目标
∣ ∣ ϵ − ϵ θ ( x t , t ) ∣ ∣ 2 = ∣ ∣ ϵ − ϵ θ ( α t ‾ x 0 + ( 1 − α t ‾ ) ϵ , t ) ∣ ∣ 2 ||\epsilon - \epsilon_{\theta}(\mathbf{x}_t, t) ||^2 = || \epsilon - \epsilon_{\theta}(\sqrt{\overline{\alpha_t}}\mathbf{x}_0 + \sqrt{(1-\overline{\alpha_t})}\epsilon, t) ||^2 ∣∣ϵ−ϵθ(xt,t)∣∣2=∣∣ϵ−ϵθ(αtx0+(1−αt)ϵ,t)∣∣2
那么,
α
t
‾
\sqrt{\overline{\alpha_t}}
αt就是代码中的sqrt_alphas_cumprod,
(
1
−
α
t
‾
)
\sqrt{(1-\overline{\alpha_t})}
(1−αt)就是代码中的sqrt_one_minus_alphas_cumprod:
# 时间步(timestep)定义为300
timesteps = 300
# 定义Beta Schedule, 选择线性版本,同DDPM原文一致,当然也可以换成cosine_beta_schedule
betas = linear_beta_schedule(timesteps=timesteps)
# 根据beta定义alpha
alphas = 1. - betas
alphas_cumprod = torch.cumprod(alphas, axis=0)
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)
sqrt_recip_alphas = torch.sqrt(1.0 / alphas)
# 计算前向过程 diffusion q(x_t | x_{t-1}) 中所需的
sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod)
sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)
def extract(a, t, x_shape):
batch_size = t.shape[0]
out = a.gather(-1, t.cpu())
return out.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device)
以网上的一个小猫为例:

from PIL import Image
import requests
url = 'http://images.cocodataset.org/val2017/000000039769.jpg'
image = Image.open(requests.get(url, stream=True).raw) # PIL image of shape HWC
image
其加噪过程对应的公式如下:
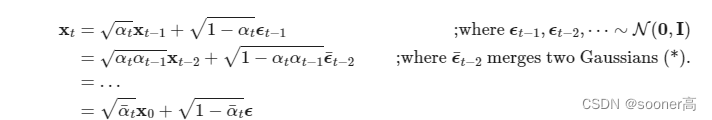
代码如下:
# 前向加噪过程: forward diffusion process
def q_sample(x_start, t, noise=None):
if noise is None:
noise = torch.randn_like(x_start)
sqrt_alphas_cumprod_t = extract(sqrt_alphas_cumprod, t, x_start.shape)
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x_start.shape
)
return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise
# 图像后处理
def get_noisy_image(x_start, t):
# add noise
x_noisy = q_sample(x_start, t=t)
# turn back into PIL image
noisy_image = reverse_transform(x_noisy.squeeze())
return noisy_image
...
# 展示图像, t=0, 50, 100, 150, 199的效果
plot([get_noisy_image(x_start, torch.tensor([t])) for t in [0, 50, 100, 150, 199]])
从左到右: 原图图像(t=0), t=50, t=100, t=150, t=199的前向加噪效果图。

6.2 网络定义&目标函数
如前面的公式推导所知,DDPM要优化的均值 μ \mu μ,经过了重参数化操作,变成了预测添加的噪声 ϵ t \epsilon_t ϵt,最终,我们要优化的损失函数 L t L_t Lt的表示如下:
∣ ∣ ϵ − ϵ θ ( x t , t ) ∣ ∣ 2 = ∣ ∣ ϵ − ϵ θ ( α t ‾ x 0 + ( 1 − α t ‾ ) ϵ , t ) ∣ ∣ 2 ||\epsilon - \epsilon_{\theta}(\mathbf{x}_t, t) ||^2 = || \epsilon - \epsilon_{\theta}(\sqrt{\overline{\alpha_t}}\mathbf{x}_0 + \sqrt{(1-\overline{\alpha_t})}\epsilon, t) ||^2 ∣∣ϵ−ϵθ(xt,t)∣∣2=∣∣ϵ−ϵθ(αtx0+(1−αt)ϵ,t)∣∣2
在实际中,对应的损失函数定义如下,其中denoise_model就是如下的UNet结构,

Phil Wang的PyTorch版代码[12]实现如下, 其目标是:
- 该U-Net将一批噪声图像/noisy image(bs, num_channels, height, width)和一批噪声水平/noise level(bs, 1)作为输入,并得到一个和噪声图像/noisy image同样维度的Tensor。
其实网络的细节不用看的很多,这里主要关注2点:
- ① 对timestep的编码和embedding传输,
SinusoidalPosEmb,self.time_mlp。 - ② Downsample和Upsample的特征的Concatenate的实现,
Concatenate。
class Unet(nn.Module):
def __init__(
self,
dim,
init_dim = None,
out_dim = None,
dim_mults=(1, 2, 4, 8),
channels = 3,
self_condition = False,
resnet_block_groups = 8,
learned_variance = False,
learned_sinusoidal_cond = False,
random_fourier_features = False,
learned_sinusoidal_dim = 16
):
super().__init__()
# determine dimensions
self.channels = channels
self.self_condition = self_condition
input_channels = channels * (2 if self_condition else 1)
init_dim = default(init_dim, dim)
self.init_conv = nn.Conv2d(input_channels, init_dim, 7, padding = 3)
dims = [init_dim, *map(lambda m: dim * m, dim_mults)]
in_out = list(zip(dims[:-1], dims[1:]))
block_klass = partial(ResnetBlock, groups = resnet_block_groups)
# time embeddings
time_dim = dim * 4
self.random_or_learned_sinusoidal_cond = learned_sinusoidal_cond or random_fourier_features
if self.random_or_learned_sinusoidal_cond:
sinu_pos_emb = RandomOrLearnedSinusoidalPosEmb(learned_sinusoidal_dim, random_fourier_features)
fourier_dim = learned_sinusoidal_dim + 1
else:
sinu_pos_emb = SinusoidalPosEmb(dim)
fourier_dim = dim
self.time_mlp = nn.Sequential(
sinu_pos_emb,
nn.Linear(fourier_dim, time_dim),
nn.GELU(),
nn.Linear(time_dim, time_dim)
)
# layers
self.downs = nn.ModuleList([])
self.ups = nn.ModuleList([])
num_resolutions = len(in_out)
for ind, (dim_in, dim_out) in enumerate(in_out):
is_last = ind >= (num_resolutions - 1)
self.downs.append(nn.ModuleList([
block_klass(dim_in, dim_in, time_emb_dim = time_dim),
block_klass(dim_in, dim_in, time_emb_dim = time_dim),
Residual(PreNorm(dim_in, LinearAttention(dim_in))),
Downsample(dim_in, dim_out) if not is_last else nn.Conv2d(dim_in, dim_out, 3, padding = 1)
]))
mid_dim = dims[-1]
self.mid_block1 = block_klass(mid_dim, mid_dim, time_emb_dim = time_dim)
self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim)))
self.mid_block2 = block_klass(mid_dim, mid_dim, time_emb_dim = time_dim)
for ind, (dim_in, dim_out) in enumerate(reversed(in_out)):
is_last = ind == (len(in_out) - 1)
self.ups.append(nn.ModuleList([
block_klass(dim_out + dim_in, dim_out, time_emb_dim = time_dim),
block_klass(dim_out + dim_in, dim_out, time_emb_dim = time_dim),
Residual(PreNorm(dim_out, LinearAttention(dim_out))),
Upsample(dim_out, dim_in) if not is_last else nn.Conv2d(dim_out, dim_in, 3, padding = 1)
]))
default_out_dim = channels * (1 if not learned_variance else 2)
self.out_dim = default(out_dim, default_out_dim)
self.final_res_block = block_klass(dim * 2, dim, time_emb_dim = time_dim)
self.final_conv = nn.Conv2d(dim, self.out_dim, 1)
def forward(self, x, time, x_self_cond = None):
if self.self_condition:
x_self_cond = default(x_self_cond, lambda: torch.zeros_like(x))
x = torch.cat((x_self_cond, x), dim = 1)
x = self.init_conv(x)
r = x.clone()
t = self.time_mlp(time)
h = []
for block1, block2, attn, downsample in self.downs:
x = block1(x, t)
h.append(x)
x = block2(x, t)
x = attn(x)
h.append(x)
x = downsample(x)
x = self.mid_block1(x, t)
x = self.mid_attn(x)
x = self.mid_block2(x, t)
for block1, block2, attn, upsample in self.ups:
x = torch.cat((x, h.pop()), dim = 1)
x = block1(x, t)
x = torch.cat((x, h.pop()), dim = 1)
x = block2(x, t)
x = attn(x)
x = upsample(x)
x = torch.cat((x, r), dim = 1)
x = self.final_res_block(x, t)
return self.final_conv(x)
损失函数一般常用的是L1, L2和Huber Loss(其实是Smooth的L1 Loss)
L1Loss PyTorch 2.0 定义:
SmoothL1Loss PyTorch 2.0 定义:
def p_losses(denoise_model, x_start, t, noise=None, loss_type="l1"):
if noise is None:
noise = torch.randn_like(x_start)
# x_noisy就是前向的加噪得到的噪声数据
x_noisy = q_sample(x_start=x_start, t=t, noise=noise)
# predicted_noise就是模型预测的噪声
predicted_noise = denoise_model(x_noisy, t)
if loss_type == 'l1':
loss = F.l1_loss(noise, predicted_noise)
elif loss_type == 'l2':
loss = F.mse_loss(noise, predicted_noise)
elif loss_type == "huber":
loss = F.smooth_l1_loss(noise, predicted_noise)
else:
raise NotImplementedError()
return loss
6.3 Dataloader & Sampling
这里参考Hugging Face的博客[13],其选择了Fashion MNIST作为例子进行最简单的展示:
from datasets import load_dataset
# load dataset from the hub
dataset = load_dataset("fashion_mnist")
image_size = 28
channels = 1
batch_size = 128
from torchvision import transforms
from torch.utils.data import DataLoader
# define image transformations (e.g. using torchvision)
transform = Compose([
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Lambda(lambda t: (t * 2) - 1)
])
# define function
def transforms(examples):
examples["pixel_values"] = [transform(image.convert("L")) for image in examples["image"]]
del examples["image"]
return examples
transformed_dataset = dataset.with_transform(transforms).remove_columns("label")
# create dataloader
dataloader = DataLoader(transformed_dataset["train"], batch_size=batch_size, shuffle=True)
Ok, 数据加载器Dataloader完成后,还需要进行Sampling的定义,从而能验证噪声预测器模型
ϵ
θ
\epsilon_{\theta}
ϵθ训练的效果(即从
x
T
→
x
0
\mathbf{x}_T \rightarrow \mathbf{x}_0
xT→x0),采样Sampling的逻辑定义如下:

从扩散模型生成新图像是通过逆转扩散过程来实现的:从
T
T
T开始,从 纯粹的高斯分布(Gaussian distribution) 中采样噪声,
然后使用我们的神经网络逐渐去噪(使用网络学到的条件概率),然后到
t
=
0
t=0
t=0结束。显然,我们可以通过插入重参数化的均值,使用我们的噪声预测器
ϵ
θ
\epsilon_{\theta}
ϵθ,得到去噪后的图像
x
t
−
1
\mathbf{x}_{t-1}
xt−1。
注意:DDPM的variance是fix的,所以这里不需要考虑variance(方差)的影响。
理想情况下,我们最终得到的图像看起来像是来自真实的数据分布, 其代码如下:
@torch.no_grad()
def p_sample(model, x, t, t_index):
betas_t = extract(betas, t, x.shape)
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x.shape
)
sqrt_recip_alphas_t = extract(sqrt_recip_alphas, t, x.shape)
# Equation 11 in the paper
# Use our model (noise predictor) to predict the mean
model_mean = sqrt_recip_alphas_t * (
x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t
)
if t_index == 0:
return model_mean
else:
posterior_variance_t = extract(posterior_variance, t, x.shape)
noise = torch.randn_like(x)
# Algorithm 2 line 4:
return model_mean + torch.sqrt(posterior_variance_t) * noise
# Algorithm 2 (including returning all images)
@torch.no_grad()
def p_sample_loop(model, shape):
device = next(model.parameters()).device
b = shape[0]
# start from pure noise (for each example in the batch)
img = torch.randn(shape, device=device)
imgs = []
for i in tqdm(reversed(range(0, timesteps)), desc='sampling loop time step', total=timesteps):
img = p_sample(model, img, torch.full((b,), i, device=device, dtype=torch.long), i)
imgs.append(img.cpu().numpy())
return imgs
@torch.no_grad()
def sample(model, image_size, batch_size=16, channels=3):
return p_sample_loop(model, shape=(batch_size, channels, image_size, image_size))
注意,上面的代码是原始实现的简化版本,Jonathon Ho的原始实现请看Tensorlflow的实现。
6.4 训练(Training)
接下来,我们以常规的PyTorch方式进行模型训练。我们还定义了一些逻辑,比如中间结果保存、定义优化器等等,这些不太重要,我们直入主题:训练脚本
from torchvision.utils import save_image
epochs = 6
for epoch in range(epochs):
for step, batch in enumerate(dataloader):
optimizer.zero_grad()
batch_size = batch["pixel_values"].shape[0]
# 1. Fashion Mnist数据集
batch = batch["pixel_values"].to(device)
# 2. 随机采样X_t
# Algorithm 1 line 3: sample t uniformally for every example in the batch
t = torch.randint(0, timesteps, (batch_size,), device=device).long()
loss = p_losses(model, batch, t, loss_type="huber")
if step % 100 == 0:
print("Loss:", loss.item())
loss.backward()
optimizer.step()
# 3. 保存中间结果
# save generated images
if step != 0 and step % save_and_sample_every == 0:
milestone = step // save_and_sample_every
batches = num_to_groups(4, batch_size)
all_images_list = list(map(lambda n: sample(model, batch_size=n, channels=channels), batches))
all_images = torch.cat(all_images_list, dim=0)
all_images = (all_images + 1) * 0.5
save_image(all_images, str(results_folder / f'sample-{milestone}.png'), nrow = 6)
可以看到其loss是在不断下降的:
Output:
----------------------------------------------------------------------------------------------------
Loss: 0.46477368474006653
Loss: 0.12143351882696152
Loss: 0.08106148988008499
...
Loss: 0.046371955424547195
Loss: 0.04952816292643547
Loss: 0.04472338408231735
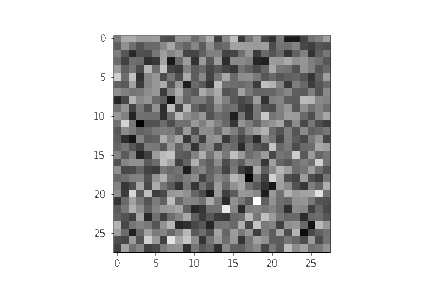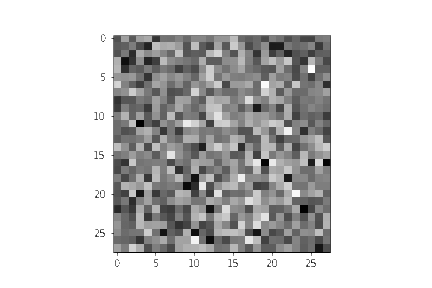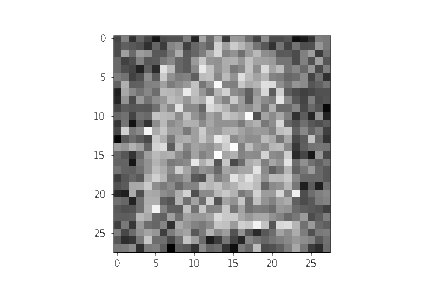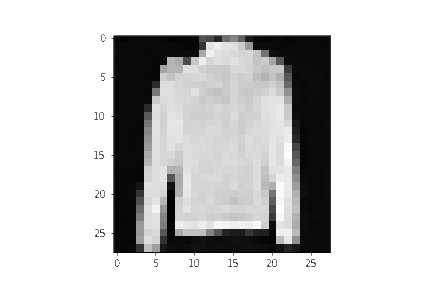
当模型训练完毕后,我们将随机从Gaussian Distribution中采样得到 x T \mathbf{x}_T xT, 然后通过reverse/backward diffusion process得到其对应的 x 0 \mathbf{x}_0 x0,代码就是6.3中的Sampling,其结果如下(图像分辨率是 28 × 28 28 \times 28 28×28):
# sample 64 images
samples = sample(model, image_size=image_size, batch_size=64, channels=channels)
# show a random one
random_index = 5
plt.imshow(samples[-1][random_index].reshape(image_size, image_size, channels), cmap="gray")
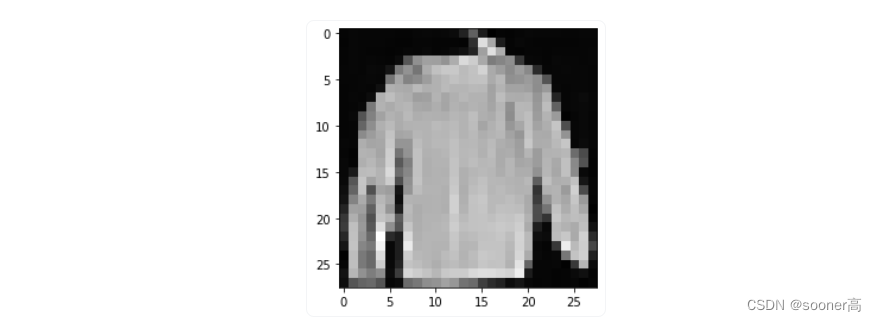
虽然清晰度不够,但是也能依稀看出,DDPM能够生成一件漂亮的t恤! 请记住,我们训练的数据集分辨率很低(28x28)。
同样地,逐渐去噪的Gif效果如下所示:
import matplotlib.animation as animation
random_index = 53
fig = plt.figure()
ims = []
for i in range(timesteps):
im = plt.imshow(samples[i][random_index].reshape(image_size, image_size, channels), cmap="gray", animated=True)
ims.append([im])
animate = animation.ArtistAnimation(fig, ims, interval=50, blit=True, repeat_delay=1000)
animate.save('diffusion.gif')
plt.show()
至此,一个DDPM的最简单的展示过程已经介绍完毕,如有有公式和代码对不上的情况,请不断的重复翻阅第4节。
7. 尾声
DDPM论文的出现,表明扩散模型是(非)条件图像生成的一个有前途的方向。从那时起,Diffusion Models已经(极大地)得到了改进,最显著的是Text2Image生成。后续有非常多的重要工作极大的提升了DDPM的效率:
-
DDIM(更快的采样/Sampling过程,可以直接从 T = 100 T=100 T=100回到 1 1 1,不需要DDPM那种迭代式的做法: ICLR 2021)
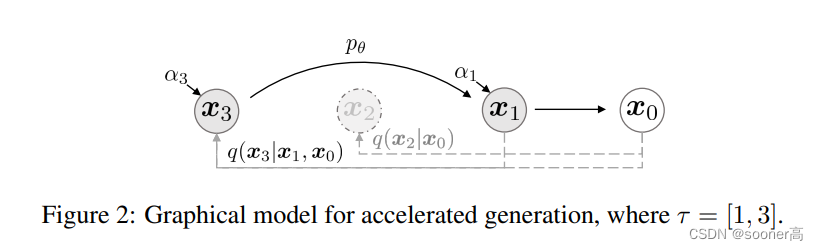
-
EDM (简化diffusion-based 生成模型, 更快的采样 NeurIPS 2022)

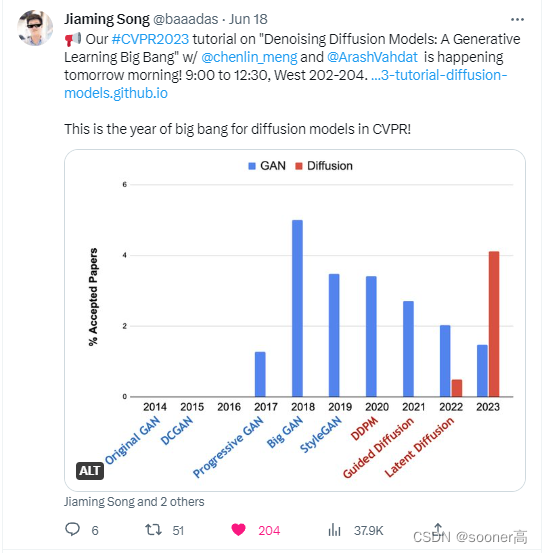
还有很多新的工作未被提及,最后以一张图结尾(DDIM作者的twitter): Diffusion Model在CVPR的接收论文比例第一次显著超出GAN!未来以来,抓紧上车吧!
参考文献
- Diffusion Models Beat GANs on Image Synthesis
- DALLE-2
- Civitai
- Midjourney
- Phil Wang的DDPM实现
- Deep Unsupervised Learning using Nonequilibrium Thermodynamics
- Introduction to Diffusion Models for Machine Learning: AssembyAI
- Auto-Encoding Variational Bayes
- Evidence lower bound-Wikipedia
- U-Net
- Improved Denoising Diffusion Probabilistic Models
- Phil Wang: DDPM’s code of UNet (PyTorch)
- The Annotated Diffusion Model

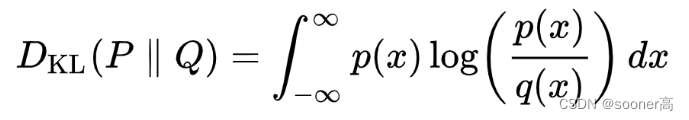
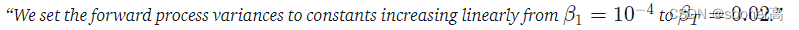
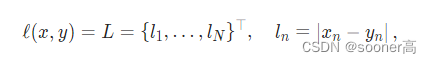
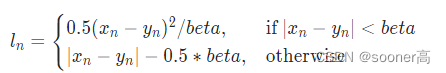

![强化学习从基础到进阶-常见问题和面试必知必答[3]:表格型方法:Sarsa、Qlearning;蒙特卡洛策略、时序差分等以及Qlearning项目实战](https://img-blog.csdnimg.cn/d553c7dadca54bdb82a3a234befb74d8.png#pic_center)