💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🌈3 Matlab代码实现

🎉4 参考文献

---

💥1 概述

当在线性等约束二次规划 （EQP） 类型中对二次项矩阵应用特征值分解时，存在线性映射以预测新 EQP 公式（其中 $Q$ 对角化）与原始公式之间的最优解。尽管这种映射需要特定类型的相等约束，但它可以推广到一些实际问题，例如投资组合分配的有效边界和最小二乘支持向量机 （LSSVM） 的分类。已建立的映射可能对探索子空间中的最优解有用，但作者还不是很清楚。这项工作的灵感来自前面在中讨论的在无约束公式上证明的类似工作，但它目前的证明得到了很大的改进和推广。

📚2 运行结果

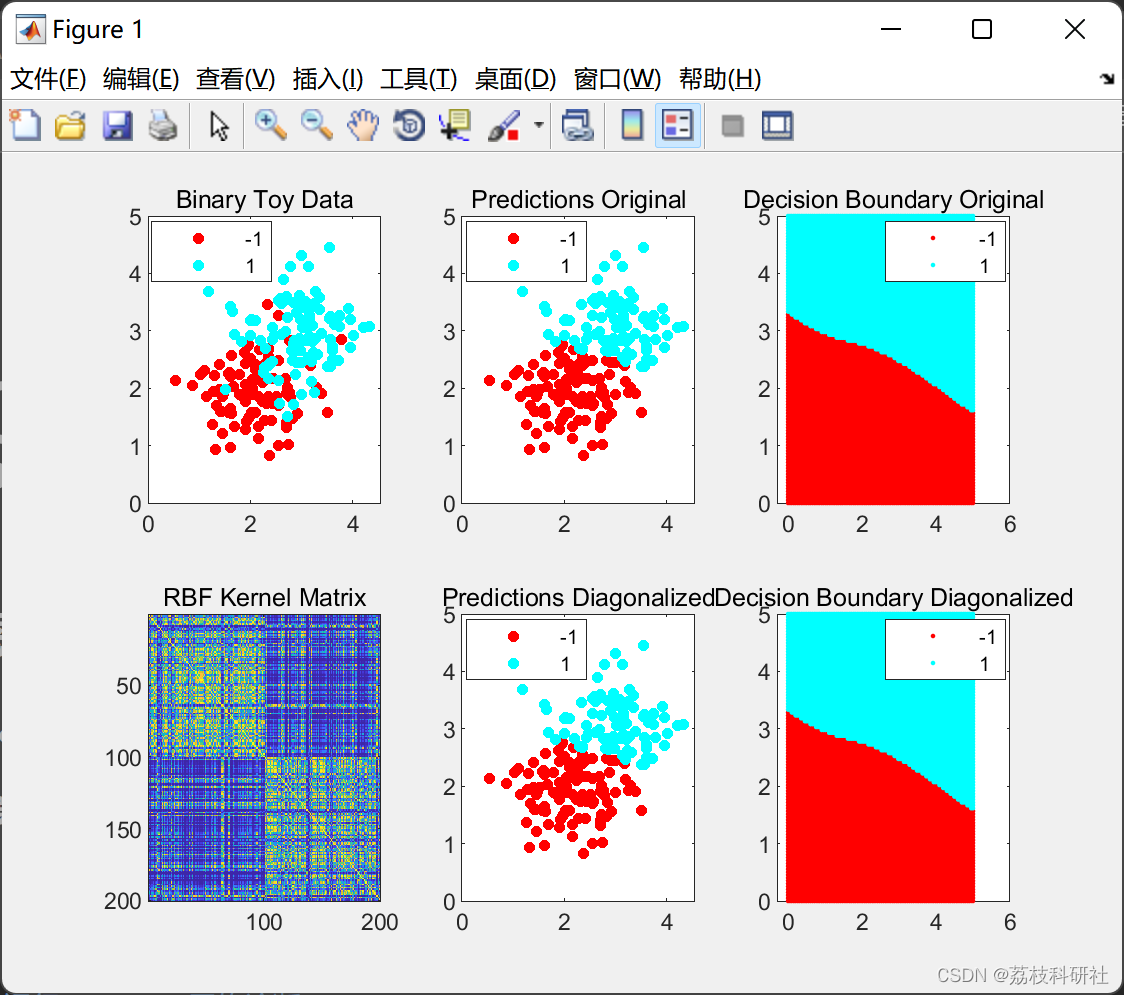
部分代码：

scatter(X(:,1),X(:,2),Y);
title('Binary Toy Data');

x = linspace(0,5);
y = linspace(0,5);
[XX,YY] = meshgrid(x,y);

pred = [XX(:),YY(:)];

n = size(X,1);
m = size(pred,1);

K = zeros(n,n);
Km = zeros(n,m);

for loop=1:1:n
    K(:,loop)=RBF_kernel(X(loop,:),X,1);
    %K(:,loop)=lin_kernel(X(loop,:),X);
end

subplot(2,3,4);
imagesc(K);
title('RBF Kernel Matrix');

gamma = 20;

K = K + 1/gamma.*eye(size(K));

for loop=1:1:m
    Km(:,loop)=RBF_kernel(pred(loop,:),X,1);
    %Km(:,loop)=lin_kernel(pred(loop,:),X);
end

onevec = ones(n,1);

xopt = optimal_sol_lssvm(K,Y', onevec);

Ypd = zeros(1,n);
Ymespd = zeros(1,m);

for loop=1:1:n
    Ypd(loop) = sign(sum(K(:,loop).*Y.*xopt));
end

for loop=1:1:m
    Ymespd(loop) = sign(sum(Km(:,loop).*Y.*xopt));
end

subplot(2,3,2);

gscatter(X(:,1),X(:,2),Ypd);
title('Predictions Original');

pred = [XX(:),YY(:)];

subplot(2,3,3);
gscatter(pred(:,1),pred(:,2), Ymespd);
title('Decision Boundary Original');

[U,V]=svd(K);

k=10;

%         Uk = U(:,1:k);
%         Vk = V(1:k,1:k);
% 
%         Ck = diag(Y'.*1./(Y'*Uk));
        
C = diag(Y'.*1./(Y'*U));
Kproj = C*C*V;
onevecproj = C*U'*onevec;

xopt_proj = optimal_sol_lssvm(Kproj,Y',onevecproj);
xopt_recover = U*C*xopt_proj;

Ypd = zeros(1,n);
Ymespd = zeros(1,m);

for loop=1:1:n
    Ypd(loop) = sign(sum(K(:,loop).*Y.*xopt_recover));
end

subplot(2,3,5);

gscatter(X(:,1),X(:,2),Ypd);
title('Predictions Diagonalized');

for loop=1:1:m
    Ymespd(loop) = sign(sum(Km(:,loop).*Y.*xopt_recover));
end
 

🌈3 Matlab代码实现

🎉4 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]Shi Yu .Eigendecomposition of Qin Equally Constrained Quadratic Programming Apr 22,2020