01背包

代码随想录理论讲解
背包问题分类
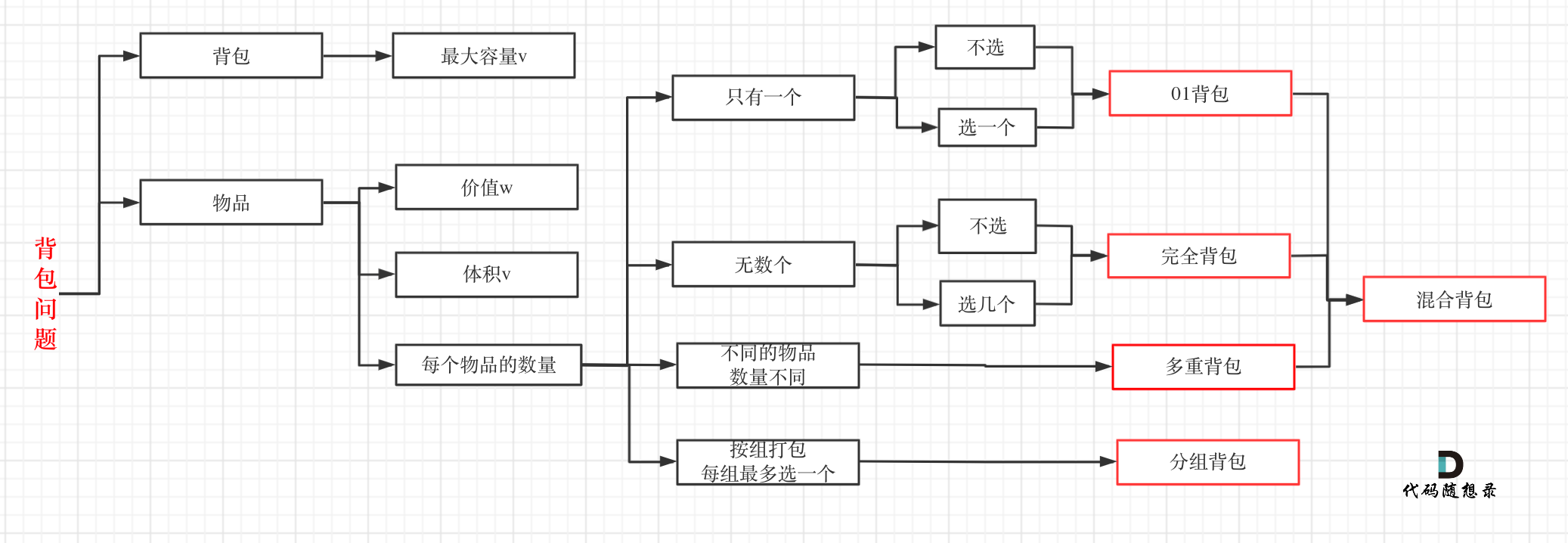
在这里插入图片描述

01背包

问题描述
有n件物品和一个最多能背重量为w的背包。第i件物品的重量是weight[i]，得到的价值是value[i]。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。
动归五部曲

确定dp数组及下标含义。二维数组dp[i][j]表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大为dp[i][j].
确定递推公式。有两个方向可以推出dp[i][j]。不放物品i:由dp[i-1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i-1]j；放物品i：由dp[i-1][j-weight[i]] + value[i]推出。递推公式为dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
数组初始化。dp[i][0] = 0;当下标为0的物品的体积小于等于背包的体积时dp[0][j] = value[0],反之dp[0][j] = 0;
确定遍历顺序。有两个遍历的纬度：物品与背包重量。对于此特定的情境“固定体积的背包装取物品的体积最大”来说，先遍历物品和先遍历背包是一样的。
举例推导dp数组。
数组初始化

vector<int> dp(weight.size(),vector<int>(bagsize+1,0));
for(int j=weight[0];j<=bagsize;++j) dp[0][j]=value[0];

先遍历物品后遍历背包

for(int i=1;i<weight.size();++i){
for(int j=1;j<=bagsize;++i){
	if(j<weight[i]) dp[i][j] = dp[i-1][j];
    else dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
	}
}

先遍历背包后遍历物品

for(int j=1;j<=bagsize;++j){
for(int i=1;i<weight.size();++i){
	if(j<weight[i]) dp[i][j] = dp[i-1][j];
    else dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
            }
        }

01背包滚动数组

压缩二维数组的状态。使用二维数组时的递推公式为dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]).
可以发现如果把dp[i-1]那一层拷贝到dp[i]上，表达式完全可以是dp[i][j] = max(dp[i][j],dp[i][j-weight[i]]+value[i])
与其把dp[i-1]这一层拷贝到dp[i]上不如只用一个一维数组，只用dpj

动规五部曲

确定dp数组及含义。dp[j]表示体积为j的背包可以装取物品的最大价值为dp[j]。
确定递推公式。不放物品i就是dp[j]，放物品i就是dp[j-weight[i]]+value[i];
数组初始化。dp[0]=0;
确定遍历顺序。由于将二维数组中的i略去变成滚动数组，所以遍历顺序应该是先遍历物品后遍历背包。并且为了满足每个物品只能选取一次或者不选取，在遍历背包的时候需要从大到小的顺序遍历。
举例推导dp数组。
先遍历物品后遍历背包

vector<int> dp(bagsize+1,0);
for(int i=0;i<weight.size();++i){
	for(int j=bagsize;j>=weight[i];--j)
		dp[j] = max(dp[j],dp[j-weight[i]]+value[i]);
}

416.分割等和子集

链接：LeetCode416.分割等和子集
把该题抽象成01背包：
首先求出所给数组nums中元素的总和sum，如果sum为奇数一定不能分割成两个元素和相等的子集。在sum为偶数的前提下，抽象成背包问题：
背包的体积为sum/2，各个物品的重量为nums[i]，各个物品的价值为nums[i]。

确定dp数组以及下标含义。dp[j]表示体积为i的背包能够装下物品的最大价值为dp[j].
确定递推公式。dp[j] = max(dp[j],dp[j-weight[i]+nums[i]]);
数组初始化。dp[0]=0;
确定遍历顺序。先遍历物品后遍历背包
举例推导dp数组。

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        for(const int&num:nums) sum+=num;
        if(sum&1) return false;
        int bagsize = sum/2;
        vector<int> dp(bagsize+1,0);
        for(int i=0;i<nums.size();++i){
            for(int j=bagsize;j>=nums[i];--j){
                dp[j] = max(dp[j],dp[j-nums[i]]+nums[i]);
            }
        }
        return dp[bagsize] == bagsize;
    }
};