6. 重建二叉树

原题链接

根据前序遍历和中序遍历 得到树

过程如下：

1. 首先根据前序遍历找到 根节点
2. 找到中序遍历中，该根节点的位置
3. 中序中 位于 根节点左边的就是 左子树，右边的就是右子树
4. 由于我们需要在中序遍历中找到根节点的位置，那么每次都需要遍历中序遍历，不如直接用unordered_map存储数值和位置
5. 便于写代码，我们可以每次把mp[根节点] 的位置 用变量表示出来

本题的代码不需要死记硬背

就需要明白

由前序确定根节点
由中序确定左右子树的个数
由左右子树的个数确定下一个根节点的位置

根据这三点去写代码即可

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:

    unordered_map<int,int> pos;

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        for (int i = 0; i < n; i ++ )
            pos[inorder[i]] = i;
        return dfs(preorder, inorder, 0, n - 1, 0, n - 1);
    }

    TreeNode* dfs(vector<int>&pre, vector<int>&in, int pl, int pr, int il, int ir)
    {
        if (pl > pr) return NULL;
        int k = pos[pre[pl]] - il;
        TreeNode* root = new TreeNode(pre[pl]);
        root->left = dfs(pre, in, pl + 1, pl + k, il, il + k - 1);
        root->right = dfs(pre, in, pl + k + 1, pr, il + k + 1, ir);
        return root;
    }
};

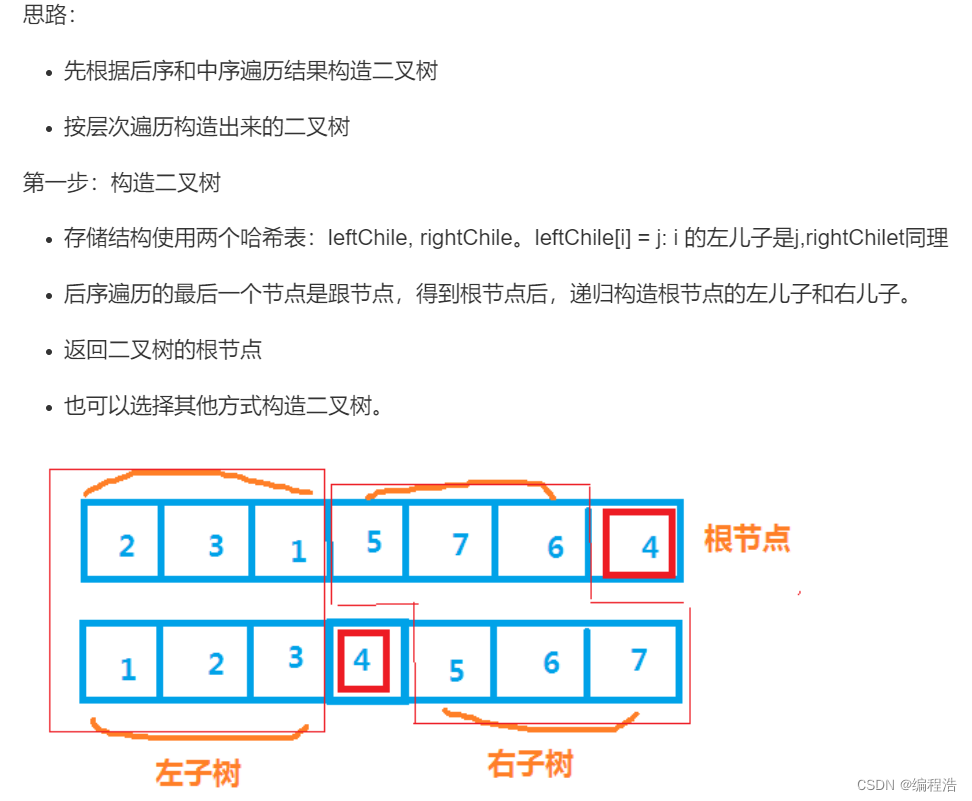
树的遍历

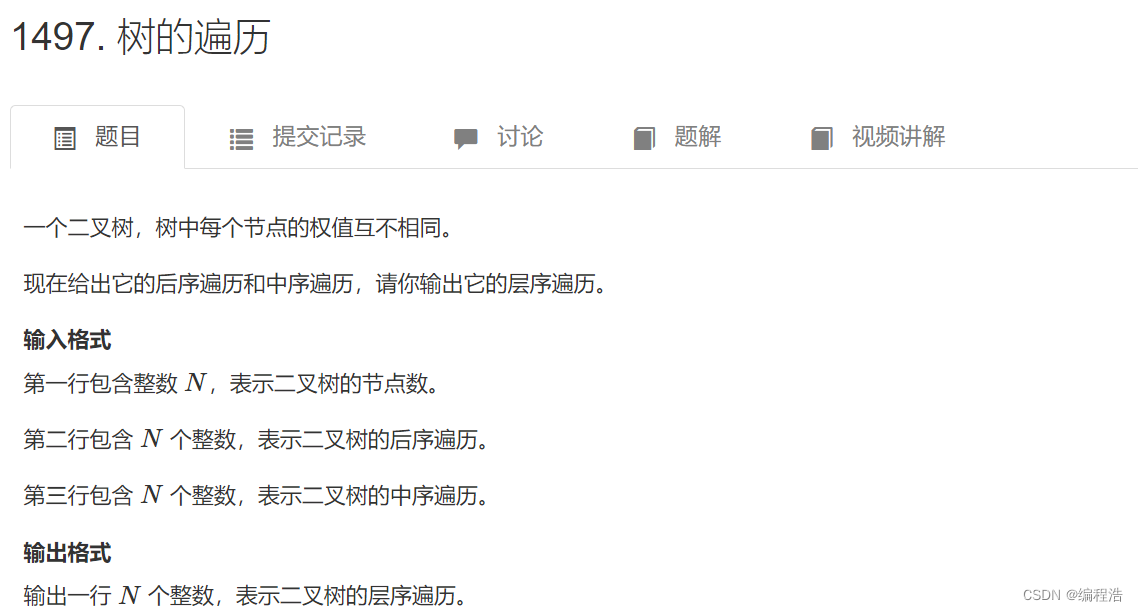
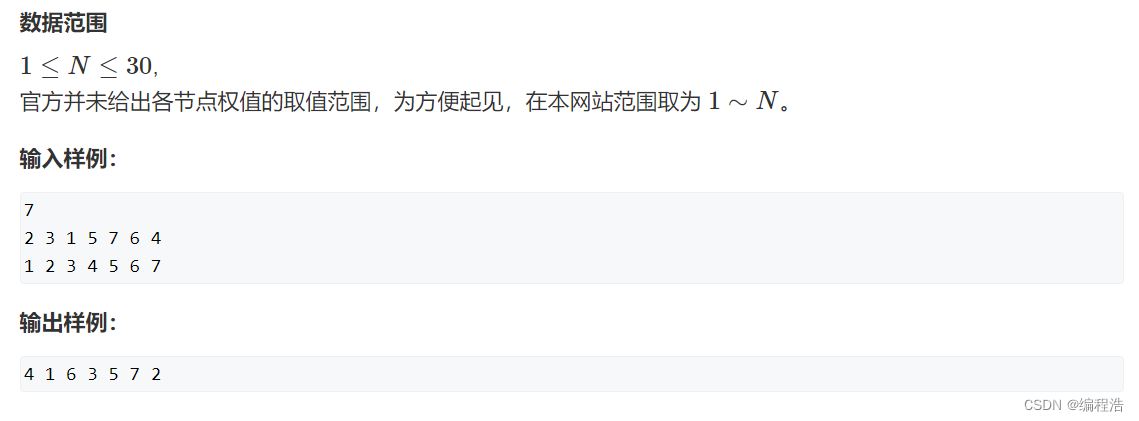
#include <iostream>
#include <string>
#include <unordered_map>
#include <vector>
#include <algorithm>
#include<memory>
using namespace std;

const  int N = 35;
int n;
int inorder[N], postorder[N];
unordered_map<int, int > leftChile, rightChile;//哈希表保存树，leftChile[i] = j: i 的左儿子是j,rightChilet同理
unordered_map<int, int > h;//保存中序遍历中各节点的位置

int dfs(int postorder[], int inorder[], int l1, int r1, int l2, int r2)//构造二叉树
{   
    if (l1 > r1) return 0;//没有节点，返回0
    int root = postorder[r1];//根结点为后续遍历的最后一个节点

    int k = h[root];//找到根节点在序遍历中的位置

    leftChile[root] = dfs(postorder, inorder, l1, k - 1 - l2 + l1, l2, k - 1);//构造左儿子
    rightChile[root] = dfs(postorder, inorder,r1-1 - (r2 - (k +1)) , r1 -1, k + 1, r2);//构造右儿子

    return root;
}

int main()
{
    cin >> n;//输入
    for (int i = 0; i < n; i++)
        cin >> postorder[i];

    for (int i = 0; i < n; i++)
    {
        cin >> inorder[i];
        h[inorder[i]] = i;//保存中序遍历中各个节点的位置
    }
    int root = dfs(postorder, inorder, 0, n - 1, 0, n - 1);//构造二叉树

    //数组模拟队列
    int q[N], hh = 0, tt = -1;//按层次遍历
    if (root)//非0 表示有节点
        q[++tt] = root;

    while (hh <= tt)
    {
        int t = q[hh++];
        if (leftChile[t]) q[++tt] = leftChile[t];//非0 为节点，入队列
        if (rightChile[t]) q[++tt] = rightChile[t];//非0 为节点，入队列
    }
    for (int i = 0; i <= tt; i++)//队列中保存的就是按层次遍历的结果
        cout << q[i] << " ";
    return 0;
}