挤压塑料胶卷的最优工艺研究
摘要
多元方差分析是同时分析多个响应变量和一个共同预测变量集之间关系的检验。与方差分析一样,多元方差分析需要连续响应变量和类别预测变量。与运行多个方差分析(一次一个响应变量)相比,多元方差分析具有多个重要优势。可以使用响应变量之间的数据协方差结构,来同时检验均值的相等性。如果响应变量彼此相关,则此附加信息有助于检测太小而无法通过单个方差分析来检测的差异。作为一个多变量过程,多元方差分析在有两个或多个因变量时使用,并且通常后面是分别涉及各个因变量的显着性检验。
- 实验步骤
第二题:
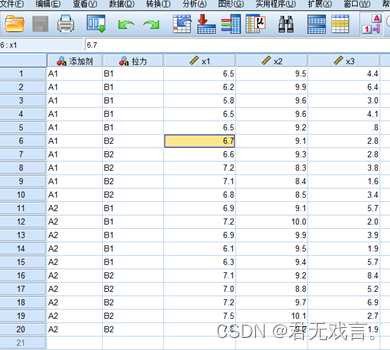
1.1 录入数据,先在spss中进行数据录入,如图:
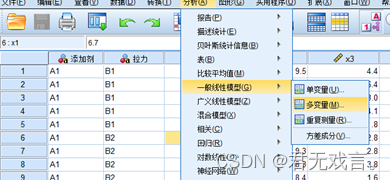
1.2 在spss里选择“分析”à“一般线性模型”à“多变量”
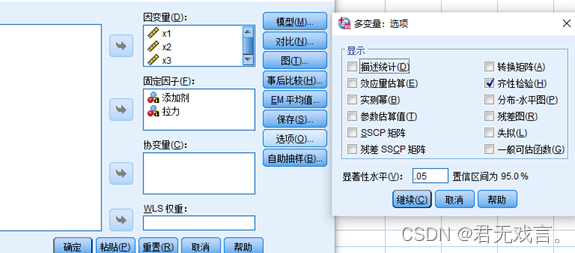
1.3 将X1,X2,X3放入因变量里面,将添加剂,拉力放入固定因子里,点击“选项”à“齐性检验”à“继续”à“确定”
- 结果分析
第二题:
| 协方差矩阵的博克斯等同性检验a | |
| 博克斯 M | 37.271 |
| F | 1.328 |
| 自由度 1 | 18 |
| 自由度 2 | 904.638 |
| 显著性 | .161 |
| 检验“各个组的因变量实测协方差矩阵相等”这一原假设。 | |
| a. 设计:截距 + 添加剂 + 拉力 + 添加剂 * 拉力 | |
1.4 显著性大于0.05,满足方差齐性
| 误差方差的莱文等同性检验a | |||||
| 莱文统计 | 自由度 1 | 自由度 2 | 显著性 | ||
| x1 | 基于平均值 | 1.919 | 3 | 16 | .167 |
| 基于中位数 | .359 | 3 | 16 | .783 | |
| 基于中位数并具有调整后自由度 | .359 | 3 | 11.183 | .784 | |
| 基于剪除后平均值 | 1.834 | 3 | 16 | .182 | |
| x2 | 基于平均值 | 1.768 | 3 | 16 | .194 |
| 基于中位数 | .475 | 3 | 16 | .704 | |
| 基于中位数并具有调整后自由度 | .475 | 3 | 12.347 | .705 | |
| 基于剪除后平均值 | 1.713 | 3 | 16 | .205 | |
| x3 | 基于平均值 | 2.133 | 3 | 16 | .136 |
| 基于中位数 | 1.761 | 3 | 16 | .195 | |
| 基于中位数并具有调整后自由度 | 1.761 | 3 | 11.902 | .208 | |
| 基于剪除后平均值 | 2.131 | 3 | 16 | .136 | |
| 检验“各个组中的因变量误差方差相等”这一原假设。 | |||||
| a. 设计:截距 + 添加剂 + 拉力 + 添加剂 * 拉力 | |||||
X1,X2,X3显著性大于0.05,满足方差齐性
| 多变量检验a | ||||||
| 效应 | 值 | F | 假设自由度 | 误差自由度 | 显著性 | |
| 截距 | 比莱轨迹 | .999 | 6023.704b | 3.000 | 14.000 | .000 |
| 威尔克 Lambda | .001 | 6023.704b | 3.000 | 14.000 | .000 | |
| 霍特林轨迹 | 1290.794 | 6023.704b | 3.000 | 14.000 | .000 | |
| 罗伊最大根 | 1290.794 | 6023.704b | 3.000 | 14.000 | .000 | |
| 添加剂 | 比莱轨迹 | .490 | 4.479b | 3.000 | 14.000 | .021 |
| 威尔克 Lambda | .510 | 4.479b | 3.000 | 14.000 | .021 | |
| 霍特林轨迹 | .960 | 4.479b | 3.000 | 14.000 | .021 | |
| 罗伊最大根 | .960 | 4.479b | 3.000 | 14.000 | .021 | |
| 拉力 | 比莱轨迹 | .608 | 7.237b | 3.000 | 14.000 | .004 |
| 威尔克 Lambda | .392 | 7.237b | 3.000 | 14.000 | .004 | |
| 霍特林轨迹 | 1.551 | 7.237b | 3.000 | 14.000 | .004 | |
| 罗伊最大根 | 1.551 | 7.237b | 3.000 | 14.000 | .004 | |
| 添加剂 * 拉力 | 比莱轨迹 | .247 | 1.533b | 3.000 | 14.000 | .250 |
| 威尔克 Lambda | .753 | 1.533b | 3.000 | 14.000 | .250 | |
| 霍特林轨迹 | .328 | 1.533b | 3.000 | 14.000 | .250 | |
| 罗伊最大根 | .328 | 1.533b | 3.000 | 14.000 | .250 | |
| a. 设计:截距 + 添加剂 + 拉力 + 添加剂 * 拉力 | ||||||
| b. 精确统计 | ||||||
截距的显著性都为0.000<0.05,说明自变量为0时,因变量不为0
| 主体间效应检验 | ||||||
| 源 | 因变量 | III 类平方和 | 自由度 | 均方 | F | 显著性 |
| 修正模型 | x1 | 2.501a | 3 | .834 | 7.563 | .002 |
| x2 | 2.457b | 3 | .819 | 4.987 | .012 | |
| x3 | 11.602c | 3 | 3.867 | .970 | .431 | |
| 截距 | x1 | 920.725 | 1 | 920.725 | 8351.243 | .000 |
| x2 | 1735.385 | 1 | 1735.385 | 10565.507 | .000 | |
| x3 | 299.538 | 1 | 299.538 | 75.143 | .000 | |
| 添加剂 | x1 | .761 | 1 | .761 | 6.898 | .018 |
| x2 | .612 | 1 | .612 | 3.729 | .071 | |
| x3 | 6.272 | 1 | 6.272 | 1.573 | .228 | |
| 拉力 | x1 | 1.741 | 1 | 1.741 | 15.787 | .001 |
| x2 | 1.301 | 1 | 1.301 | 7.918 | .012 | |
| x3 | .128 | 1 | .128 | .032 | .860 | |
| 添加剂 * 拉力 | x1 | .000 | 1 | .000 | .005 | .947 |
| x2 | .544 | 1 | .544 | 3.315 | .087 | |
| x3 | 5.202 | 1 | 5.202 | 1.305 | .270 | |
| 误差 | x1 | 1.764 | 16 | .110 | ||
| x2 | 2.628 | 16 | .164 | |||
| x3 | 63.780 | 16 | 3.986 | |||
| 总计 | x1 | 924.990 | 20 | |||
| x2 | 1740.470 | 20 | ||||
| x3 | 374.920 | 20 | ||||
| 修正后总计 | x1 | 4.266 | 19 | |||
| x2 | 5.085 | 19 | ||||
| x3 | 75.382 | 19 | ||||
| a. R 方 = .586(调整后 R 方 = .509) | ||||||
| b. R 方 = .483(调整后 R 方 = .386) | ||||||
| c. R 方 = .154(调整后 R 方 = -.005) | ||||||
添加剂浓度对x1的显著性小于0.05,对x2,x3的显著性大于0.05,说明添加剂浓度对塑料胶卷耐力有显著影响,对光泽与不透明度无显著影响。拉力对x1,x2的显著性小于0.05,对x3的显著性大于0.05,说明拉力对塑料胶卷耐力,光泽有显著影响,对不透明度无显著影响。即添加剂浓度和拉力对塑料胶卷耐力都有显著影响,拉力对光泽有显著影响,剂浓度和拉力对不透明度无显著影响
- 讨论
在多元方差分析中,因子可能影响响应之间的关系,而不会影响单个响应。方差分析不会检测这些多变量形式。多元方差分析的条件是:各个变量的每个水平必须是独立的随机样本,服从正态分布且各总体方差相等。因变量和协变量必须是数值型变量且协变量与因变量相关。自变量可以是数值型分类变量,也可以是字符型分类变量,这是方差分析的基本条件。