1.为什么要学习变换？

1.很多动画都是由各种各样的变化合成在一块的

2.摄像：将三维空间中的场景变为二维，也就是投影

2.变换的几种形式

1.缩放

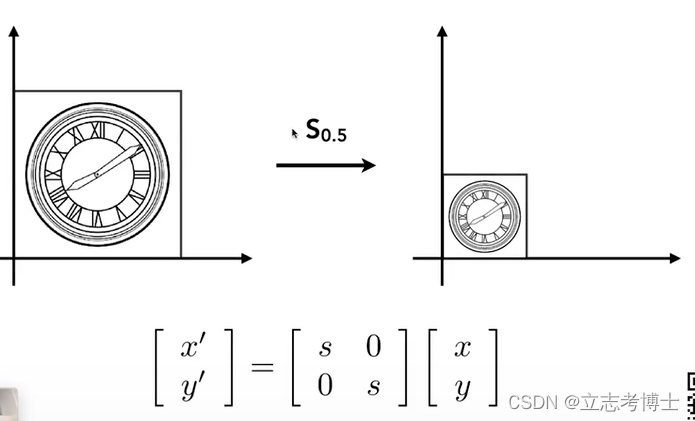
非均匀缩放

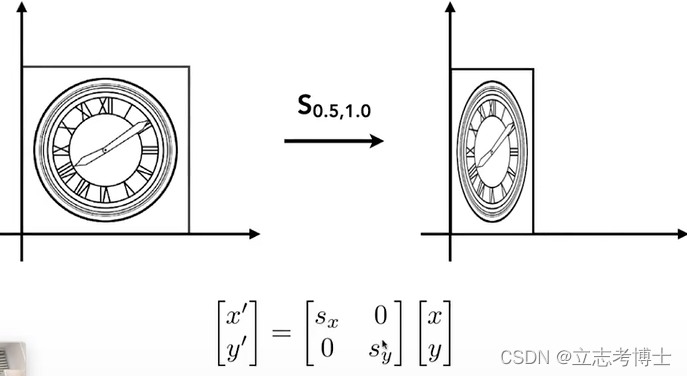
2.相对于y轴翻转

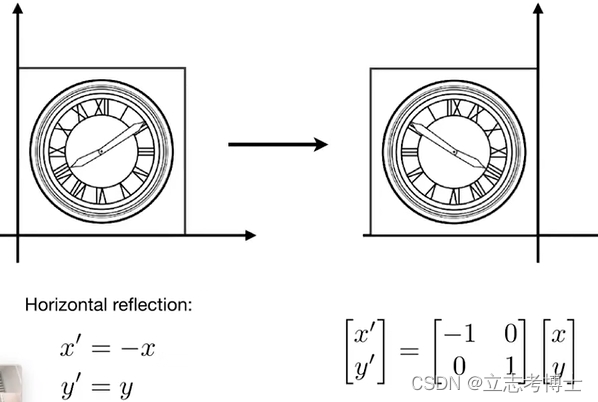
3.Shear Matrix 切片

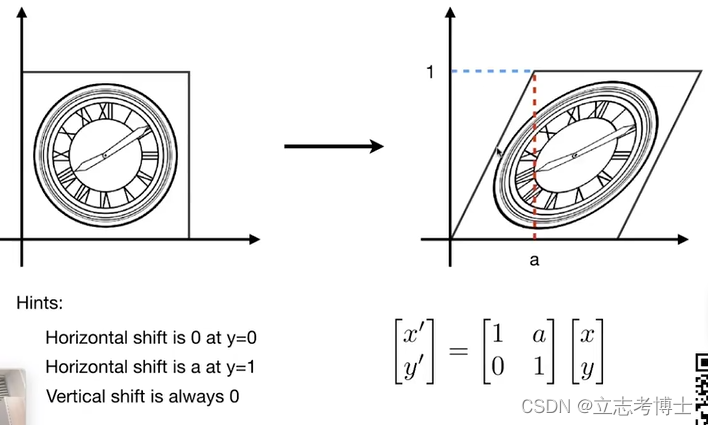
只有水平方向发生了移动，竖直方向并没有发生移动。也就是y·=y；

在最上面那条线x移动了1+a；

中间那部分移动了a*y个距离点；

4.旋转

1.使用一个特殊的点（1，0）推出A和C的值

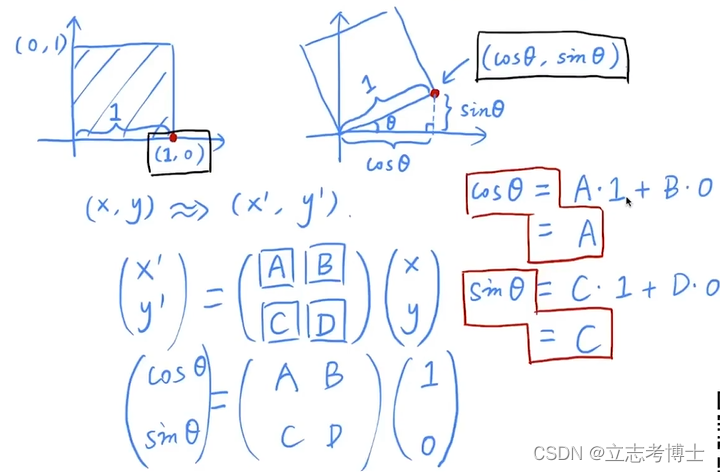
2.同理使用（0，1）推出B和D的值

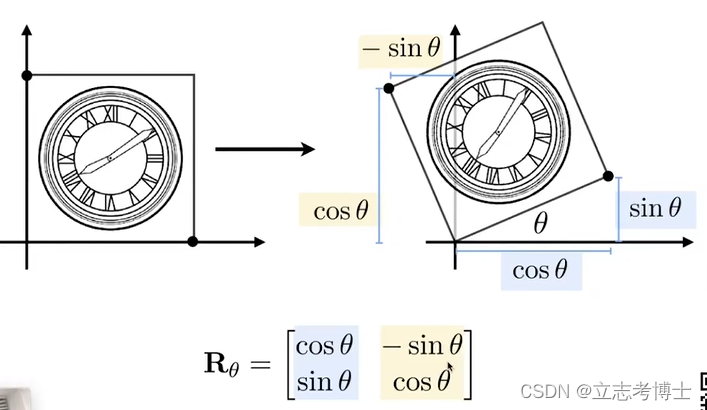
3.以上的变换都称为线性变换

3.齐次坐标

1.平移变换

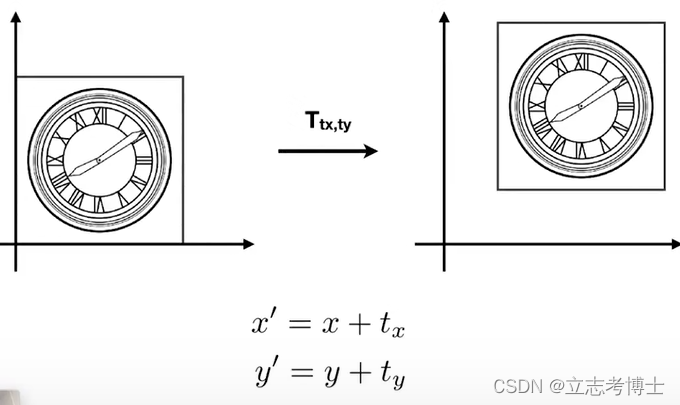
无法将这个变换写为矩阵相乘的形式，也就是说平移不是线性变换，而是仿射变换

那么有没有办法把所有的变换用统一的格式来运算？

2.齐次坐标的引入

1.对于任意一个点，我们写为（x,y,1）的竖向矩阵；

2.对于任意一个向量，我们写为（x,y,0）的竖向矩阵；

那么平移变换就可以使用相乘的形式来进行运算：

疑问：为什么对向量来说最后一位是0呢？

因为向量具有平移不变性，我们需要保证向量的方向不发生变换

3.一个点加另一个点表示的是这两个点的中点。

3.使用齐次坐标表示上述变换

1.齐次坐标形式

2.使用齐次坐标表示2D图片的缩放，旋转，平移

4.组合变换

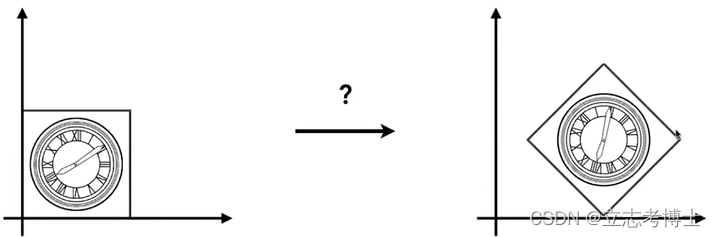
1.复杂的变换可以通过一系列简单的变换得到；

2.这些简单变换是分先后顺序的，先平移后旋转得到的结果是错误的。

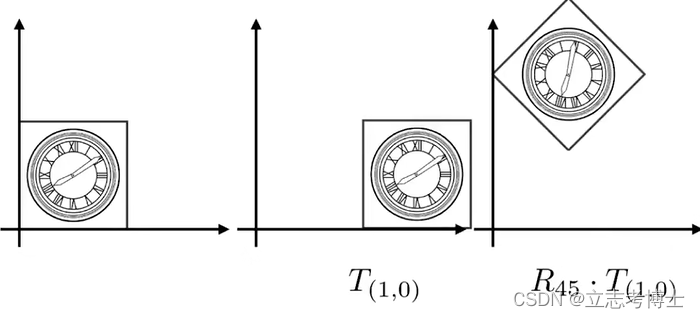
先旋转后平移得到的是想要的结果。

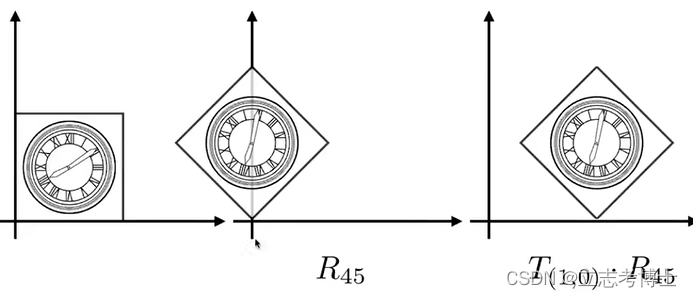
运算的顺序：从右到左

不论有多少复杂的操作，到最后都可以以一个3*3矩阵的形式去乘以xyz。

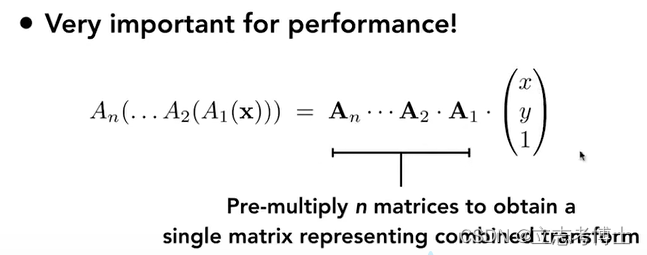
5.分解变换

1.先将没有在原点的图形移动到原点

2.然后做旋转操作

3.最后再平移回去

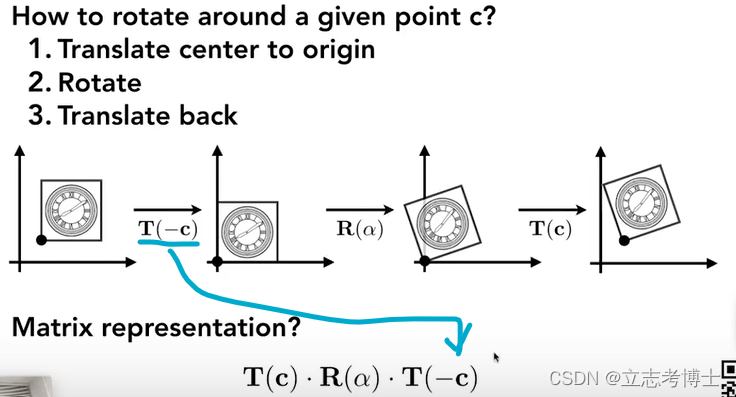
6.三维空间中的变换

1.三维空间中的点和向量

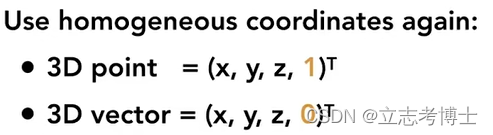
2.三维空间中的齐次坐标

组合变换时依然是先应用线性变换再平移。