前言

XGBoost属于Boosting集成学习模型，由华盛顿大学陈天齐博士提出，因在机器学习挑战赛中大放异彩而被业界所熟知。相比越来越流行的深度神经网络，XGBoost能更好的处理表格数据，并具有更强的可解释性，还具有易于调参、输入数据不变性等优势。本文只做XGBoost分类任务的脚本实现，更多XGBoost内容请查看文末附加——深入学习XGBoost

机器学习实践(1.1)XGBoost分类任务

❤️ 本文完整脚本点此链接百度网盘链接获取 ❤️

一.轻松实现回归任务

1.1导入第三方库、数据集

"""第三方库导入"""
from xgboost import XGBRegressor
from sklearn import datasets
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import r2_score, mean_squared_error
import xgboost as xgb

"""波士顿房价数据集导入"""
data = datasets.load_boston()
# print(data)

"""训练集 验证集构建"""
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target, test_size=0.2,
                                                    random_state=42)

sklearn的波士顿房价数据集共506个数据样本，8:2切分后，训练集404个数据样本，验证集102个数据样本。数据集中包括样本特征data（13个特征）、特征名称feature_names、样本标签target（MEDV）、以及数据集位置filename（~~~\anaconda\lib\site-packages\sklearn\datasets\data\boston_house_prices.csv）

特征名称和标签解释如下：

- CRIM     per capita crime rate by town\n      # 按城镇划分的犯罪率  
- ZN       proportion of residential land zoned for lots over 25,000 sq.ft.\n  # 划分为25000平方英尺以上地块的住宅用地比例        
- INDUS    proportion of non-retail business acres per town\n     # 每每个城镇的非零售商业用地比例
- CHAS     Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)\n        # 靠近查尔斯河，则为1；否则为0
- NOX      nitric oxides concentration (parts per 10 million)\n      # 一氧化氮浓度（百万分之一）
- RM       average number of rooms per dwelling\n  # 每个住宅的平均房间数      
- AGE      proportion of owner-occupied units built prior to 1940\n     # 1940年之前建造的自住单位比例  
- DIS      weighted distances to five Boston employment centres\n     # 到波士顿五个就业中心的加权距离
- RAD      index of accessibility to radial highways\n    # 辐射状公路可达性指数    
- TAX      full-value property-tax rate per $10,000\n   # 每10000美元的全额财产税税率
- PTRATIO  pupil-teacher ratio by town\n    # 按城镇划分的师生比例    
- B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town\n  # 1000（Bk-0.63）^2其中Bk是按城镇划分的黑人比例       
- LSTAT    % lower status of the population\n    # 人口密度   
- MEDV     Median value of owner-occupied homes in $1000's\n # 住房屋的中值（单位：1000美元）

1.2模型训练

"""模型训练"""
model = XGBRegressor()

# model = XGBRegressor(booster='gbtree',  # gblinear
#                      n_estimators=150,  # 迭代次数
#                      learning_rate=0.01,  # 步长
#                      max_depth=10,  # 树的最大深度
#                      min_child_weight=0.5,  # 决定最小叶子节点样本权重和
#                      seed=123,  # 指定随机种子，为了复现结果
#                      )

model.fit(X_train, y_train, verbose=True)

XGBRegressor()是没有指定参数，模型使用默认参数如下。也可以指定参数例如指定booster='gbtree'等。

learning_rate: float = 1.0,
subsample: float = 0.8,
colsample_bynode: float = 0.8,
reg_lambda: float = 1e-5,
**kwargs: Any

1.3模型验证

模型效果的验证，简单直接的可以通过验证集来实现。实际项目中通常将整个数据集按照7:3:1比例划分为训练集、验证集、测试集。本例使用验证集验证模型准确性。
回归任务的评估指标只要有 r2_score 和 mse，其中 r2_score 越趋近于1越好，mse 越小越好。
R2 【注释1】 = 1 - (SSE / TSS)，其中，SSE(sum of squared errors 【注释2】)是模型预测值与实际观测值之间差异的平方和，TSS(total sum of squares【注释2】)是所有观测值与其均值差异的平方和。

y_pred = model.predict(X_test)
# print(y_pred)

for m, n in zip(y_pred, y_test):
    if m / n - 1 > 0.2:
        print('预测值为{0}, 真是结果为{1}, 预测结果偏差大于20%'.format(m, n))


def metrics_sklearn(y_valid, y_pred_):
    """模型效果评估"""
    r2 = r2_score(y_valid, y_pred_)
    print('r2_score:{0}'.format(r2))

    mse = mean_squared_error(y_valid, y_pred_)
    print('mse:{0}'.format(mse))


"""模型效果评估"""
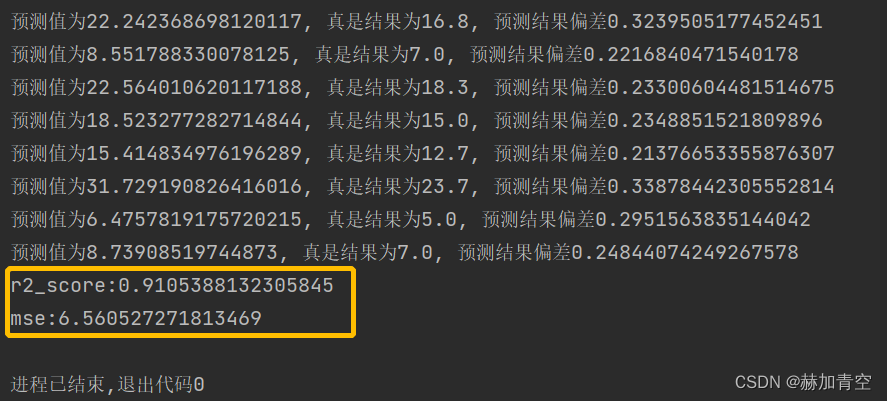
metrics_sklearn(y_test, y_pred)

结果中仅打印了预测误差在20%以上的预测数据。
在这里插入图片描述

二.模型调参

def adj_params():
    """模型调参"""
    params = {
              'booster': ['gbtree', 'gblinear'],
              # 'n_estimators': [20, 50, 100, 150, 200],
              'n_estimators': [75, 125, 200, 250, 300],
              'learning_rate': [0.01, 0.03, 0.05, 0.1],
              'max_depth': [5, 8, 10, 12]
              }

    # model_adj = XGBRegressor()

    other_params = {'subsample': 0.8, 'colsample_bytree': 0.8, 'seed': 123}
    model_adj = XGBRegressor(**other_params)

    # sklearn提供的调参工具，训练集k折交叉验证(消除数据切分产生数据分布不均匀的影响)
    optimized_param = GridSearchCV(estimator=model_adj, param_grid=params, scoring='r2', cv=5, verbose=1)
    # 模型训练
    optimized_param.fit(X_train, y_train)

    # 对应参数的k折交叉验证平均得分
    means = optimized_param.cv_results_['mean_test_score']
    params = optimized_param.cv_results_['params']
    for mean, param in zip(means, params):
        print("mean_score: %f,  params: %r" % (mean, param))
    # 最佳模型参数
    print('参数的最佳取值：{0}'.format(optimized_param.best_params_))
    # 最佳参数模型得分
    print('最佳模型得分:{0}'.format(optimized_param.best_score_))


adj_params()

2.1调参过程

第1次调参，选择'booster': ['gbtree', 'gblinear']和'n_estimators': [75, 125, 200, 250, 300]，params如下：

params = {
        'booster': ['gbtree', 'gblinear'],
        # 'n_estimators': [20, 50, 100, 150, 200],
        'n_estimators': [75, 125, 200, 250, 300],
        # 'learning_rate': [0.01, 0.03, 0.05, 0.1],
        # 'max_depth': [5, 8, 10, 12]
    }

other_params = {'seed': 123}

由结果可以显著判断，booster='gbtree'的结果显著高于booster='gblinear'
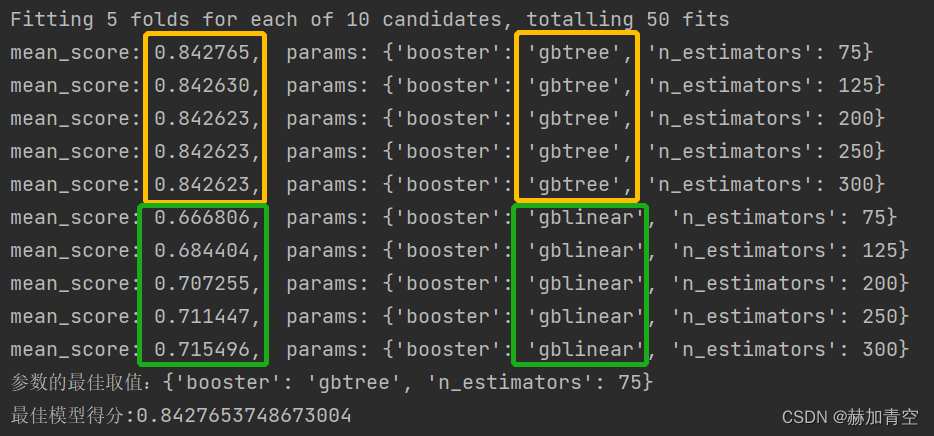
在这里插入图片描述
第2次调参，选择'n_estimators': [75, 125, 200, 250, 300]和'learning_rate': [0.01, 0.03, 0.05, 0.1]，params如下：

params = {
        # 'booster': ['gbtree', 'gblinear'],
        # 'n_estimators': [20, 50, 100, 150, 200],
        'n_estimators': [75, 125, 200, 250, 300],
        'learning_rate': [0.01, 0.03, 0.05, 0.1],
        # 'max_depth': [5, 8, 10, 12]
    }

    # model_adj = XGBRegressor()

    other_params = {'booster': 'gbtree', 'seed': 123}

由结果可以显著判断，learning_rate学习率0.01时模型效果最差，0.03~0.1之间差异不大。n_estimators迭代次数增加模型效果会明显变好。
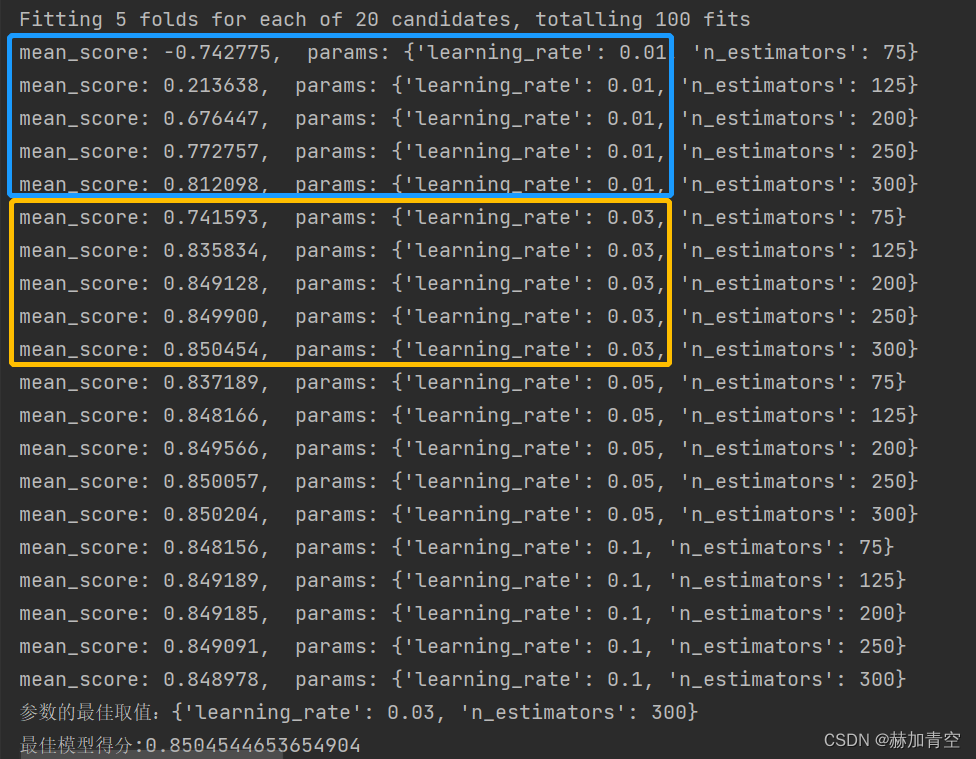在这里插入图片描述第3次调参，…
第4次调参，…

调参是个无穷无尽的过程，适可而止，切误沉溺其中本末倒置，真正决定模型效果上限的还是数据质量

2.2调参结果入模

model = XGBRegressor(booster='gbtree',  # gblinear
                     n_estimators=300,  # 迭代次数
                     learning_rate=0.03,  # 步长
                     # max_depth=10,  # 树的最大深度
                     # min_child_weight=0.5,  # 决定最小叶子节点样本权重和
                     seed=123,  # 指定随机种子，为了复现结果
                     )

model.fit(X_train, y_train, verbose=True)

基础模型booster='gbtree'，学习率learning_rate=0.03，迭代次数n_estimators=300 参数入模，fit()训练带参的模型，模型的参数和评估见下方（三.模型保存、加载、调用预测）

三.模型保存、加载、调用预测

"""模型保存"""
model.save_model('xgb_regressor_boston.model')

"""模型加载"""
clf = XGBRegressor()
clf.load_model('xgb_regressor_boston.model')

"""模型参数打印"""
bst = xgb.Booster(model_file='xgb_regressor_boston.model')

# print(bst.attributes())
print('模型参数值-开始'.center(20, '='))
for attr_name, attr_value in bst.attributes().items():
    # scikit_learn 的参数逐一解析
    if attr_name == 'scikit_learn':
        import json

        dict_attr = json.loads(attr_value)
        # 打印 模型 scikit_learn 参数
        for sl_name, sl_value in dict_attr.items():
            if sl_value is not None:
                print(f"{sl_name}:{sl_value}")
    else:
        print(f"{attr_name}:{attr_value}")
print('模型参数值-结束'.center(20, '='))

"""预测验证数据"""
y_pred = clf.predict(X_test)

"""模型效果评估"""
metrics_sklearn(y_test, y_pred)

模型参数打印和预测评估结果如图，不再赘述。
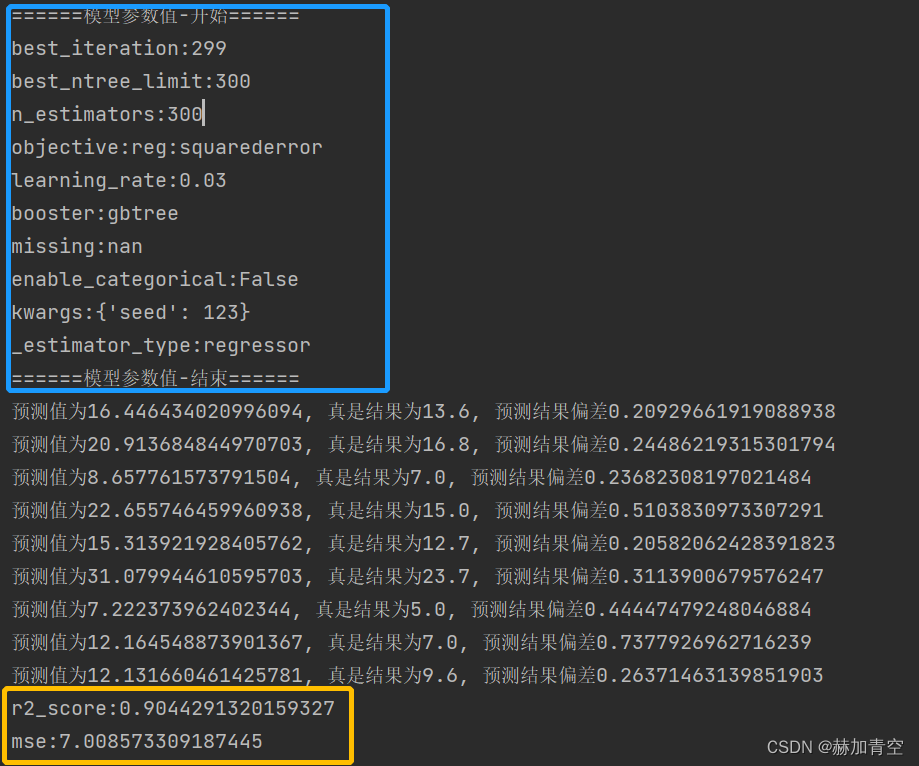
在这里插入图片描述

内容解释：

【注释1】R-squared（R2）分数是回归模型性能的一种常见评估指标。它测量模型对观测数据的拟合程度。该分数介于0和1之间，越接近1表示模型对数据的拟合越好。具体来说，R2分数是观测数据和回归模型之间差异的比率。这个比率由1减去误差平方和(SSE)和总偏差平方和(TSS)之比得到。

计算公式为：

R2 = 1 - (SSE / TSS)

其中，SSE(sum of squared errors)是模型预测值与实际观测值之间差异的平方和，TSS(total sum of squares)是所有观测值与其均值差异的平方和。

【注释2】SSE和TSS是回归分析中常用的两个指标，分别代表回归模型的误差平方和和总偏差平方和。
SSE（Sum of Squared Errors）是指在回归分析中，对于给定的自变量，在模型中计算出的因变量值与实际观察值之间的误差，即模型拟合的不准确程度。SSE等于所有误差的平方和，可以通过对每个数据点的误差（预测值与实际值之差）的平方求和得到。SSE越小，代表回归模型与实际观察值的拟合程度越好。
TSS（Total Sum of Squares）是指将每个数据点的实际观察值和所有观察值的平均值之差的平方求和，这个值代表了数据的总方差，即数据中每个点偏离数据的平均值的程度。TSS用于评估模型的预测能力，因为它反映了实际观察值的变化范围。TSS越小，代表数据相对于它的平均值离散程度越小。

计算公式如下：

SSE = sum((y_true - y_pred) ** 2)

TSS = sum((y_true - np.mean(y_true)) ** 2)

其中，y_true为真实观察值，y_pred为模型预测值，np.mean(y_true)为真实观察值的均值。

附加——深入学习XGBoost

附加1.模型调参、训练、保存、评估和预测

见《XGBoost模型调参、训练、评估、保存和预测》，包含模型脚本文件

附加2.算法原理

见《XGBoost算法原理及基础知识》，包括集成学习方法，XGBoost模型、目标函数、算法，公式推导等

附加3.分类任务的评估指标值详解

见《分类任务评估1——推导sklearn分类任务评估指标》，其中包含了详细的推理过程；
见《分类任务评估2——推导ROC曲线、P-R曲线和K-S曲线》，其中包含ROC曲线、P-R曲线和K-S曲线的推导与绘制；

附加4.模型中树的绘制和模型理解

见《Graphviz绘制模型树1——软件配置与XGBoost树的绘制》，包含Graphviz软件的安装和配置，以及to_graphviz()和plot_trees()两个画图函数的部分使用细节；
见《Graphviz绘制模型树2——XGBoost模型的可解释性》，从模型中的树着手解释XGBoost模型，并用EXCEL构建出模型。

❤️ 机器学习内容持续更新中… ❤️

声明：本文所载信息不保证准确性和完整性。文中所述内容和意见仅供参考，不构成实际商业建议，可收藏可转发但请勿转载，如有雷同纯属巧合。