【剑指offer专项突破版】队列篇——“C“

news2024/9/28 21:19:48

文章目录

  • 前言
  • 一、滑动窗口的平均值
    • 题目分析
    • 思路分析
    • 对列代码
    • 题解代码
  • 二、最近请求次数
    • 题目分析
    • 思路分析
    • 队列代码
    • 题解代码
  • 三、往完全二叉树添加节点
    • 题目分析
    • 思路分析
    • 队列与接口代码
    • 题解代码
  • 四、二叉树每层的最大值
    • 题目分析
    • 思路分析
    • 队列代码
    • 题解代码
  • 五、二叉树最底层最左边的值
    • 题目分析
    • 思路分析
    • 代码
  • 六、二叉树的右侧视图
    • 题目分析
    • 思路分析
    • 代码
  • 总结

前言

剑指offer专项突破版（力扣官网）——> 点击进入
本文所属专栏——>点击进入

一、滑动窗口的平均值

题目分析

在这里插入图片描述

思路分析

 由当大于size个时，返回最新的size个数的平均值，这符合对列的先进先出 。为了更好的理解，我们把这里的size换成容量capacity,而size这里我们认为是当前滑动窗口的当前元素个数。
因此我们可以用对列进行解题，当size小于capacity时,我们只需要入队列即可。当size等于capacity时，我们需要出队列，再进行入对列。当然，在入队列时，我们可以顺便求一下和，出队列时，和要减去对列的元素。

对列代码

typedef struct QNode
{
    struct QNode *next;
    struct QNode *prev;
    int val;
}QNode;
typedef struct 
{
    QNode* head;
    int sum;//为了方便记录我们这里采用插一个就记录当前的和
    int capacity;//这是给定的最大容量
    int size;//这是当前的size
}MovingAverage;
QNode* BuyNode(int val)
{
    QNode* NewNode = (QNode*)malloc(sizeof(QNode));
    NewNode->val = val;
    NewNode->next = NULL;
    NewNode->prev = NULL;
    return NewNode;
}
//需要写一个头插和尾删
void PushFront(QNode** head,int val)
{
    if(head == NULL)
    {
        printf("头插传入指针为空！\n");
        return;
    }
    QNode* New = BuyNode(val);
    QNode* Head = *head;
    
    if(Head == NULL)
    {
        //链表为空
        New->next = New;
        New->prev = New;
    }
    else
    {
        //进行头插操作
        New->next = Head;
        New->prev = Head->prev;

        
        Head->prev->next = New; 
        Head->prev = New;
    }
    *head = New;
}
void PopBack(QNode** head)
{
    QNode* Head = *head;
    QNode* Tail = Head->prev;
    //看是否只有一个结点
    if(Tail == Head)
    {
        *head = NULL;
    }
    else
    {
        Head->prev = Tail->prev;
        Tail->prev->next = Head;
    }
    free(Tail);
}
void QFree(QNode** head)
{
    QNode *Head = *head;
    if(Head != NULL)
    {
        QNode* cur = Head->next;
        while(cur != Head)
        {
            QNode* next = cur->next;
            free(cur);
            cur = next;
        }
    }
    free(Head);
}

题解代码

MovingAverage* movingAverageCreate(int size) 
{
    MovingAverage* init = \
     (MovingAverage*)malloc(sizeof(MovingAverage));
     // 说明:\是续行符,这里是为了防止代码过长。
    init->head = NULL;
    init->capacity = size;
    init->size = 0;
    init->sum = 0;

    return init;
}

double movingAverageNext(MovingAverage* obj, int val) 
{
    PushFront(&(obj->head),val);
    (obj->sum)+=val;
    (obj->size)++;
    //当这里的size会大于capacity
    if(obj->size > obj->capacity)
    {
        int tail = (obj->head)->prev->val;
        PopBack(&(obj->head));
        (obj->sum)-=tail;
        (obj->size)--;
    }
    double average = (double)(obj->sum)/(obj->size);
    return average;
}

void movingAverageFree(MovingAverage* obj) 
{
    QFree(&(obj->head));
    free(obj);
}

二、最近请求次数

题目分析

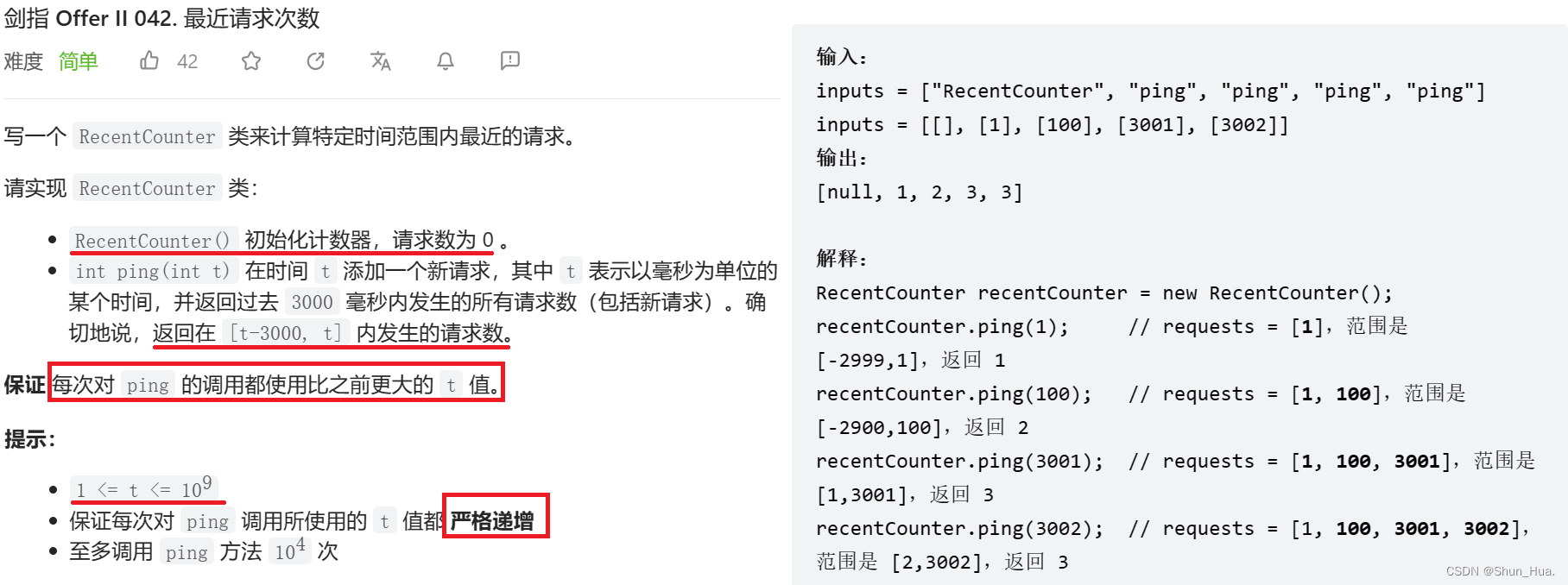
在这里插入图片描述

思路分析

 给定时间t,返回[t-3000,t]的请求次数，再加上每次请求的 t，都会严格递增,因此 t-3000会逐渐增大，因此可能有以前的t,不符合此状态。由此当有最开始的t 不符合此状态时，在此范围的请求数就减一。以前的 t 需要删除，符合先进先出，因此采用对列。因此我们只需拿当前的t-3000,跟最开始的t比较，如果大，就出对列，如果小，就入对列。当前对列的个数，即为最近请求数。

队列代码

typedef struct QNode
{
    struct QNode* prev;
    struct QNode* next;
    int top;
}QNode;

QNode* BuyNode(int top,int bottom)
{
    QNode* NewNode = (QNode*)malloc(sizeof(QNode));
    NewNode->top = top;
    NewNode->prev = NULL;
    NewNode->next = NULL;
    return NewNode;
}
void PushFront(QNode** head,int t)
{
    QNode* New = BuyNode(t,t-3000);
    QNode* Head = *head;
    if(Head == NULL)
    {
        New->next = New;
        New->prev = New;
    }
    else
    {
        New->next = Head;
        New->prev = Head->prev;

        Head->prev->next = New;
        Head->prev = New;
    }
    *head = New;
}
void PopBack(QNode** head)
{
    QNode* Head = *head;
    QNode* Tail = Head->prev;
    if(Head == Tail)
    {
        *head = NULL;
    }
    else
    {
        Head->prev = Tail->prev;
        Tail->prev->next = Head;
    }
    free(Tail);
}
void QFree(QNode** head)
{
    QNode* Head = *head;
    if(Head != NULL)
    {
        QNode* cur = Head->next;
        while(cur!=Head)
        {
            QNode* next = cur->next;
            free(cur);
            cur = next;
        } 
    }
    free(Head);
}
int Top(QNode** head)
{
    return (*head)->prev->top; 
}

bool is_empty(QNode** head)
{
    if(*head == NULL)
    {
        return true;
    }
    return false;
}

题解代码

typedef struct 
{
    QNode* head;
    int count;
}RecentCounter;
RecentCounter* recentCounterCreate() 
{
    RecentCounter* init =\
    (RecentCounter*)malloc(sizeof(RecentCounter));
    
    init->head = NULL;
    init->count = 0;
    return init;
}
int recentCounterPing(RecentCounter* obj, int t) 
{
    //先进行出栈，将范围小的出对列
    while(!is_empty(&(obj->head))&& (t-3000) > Top(&(obj->head)))
    {
        PopBack(&(obj->head));
        (obj->count)--;
    }
    //再将其入栈
    PushFront(&(obj->head),t);
    return ++(obj->count);
}
void recentCounterFree(RecentCounter* obj) 
{
    QFree(&(obj->head));
    free(obj);
}

三、往完全二叉树添加节点

题目分析

在这里插入图片描述
理论知识：

二叉树——理论篇
二叉树——顺序结构
点击即可进入

补充：
本题所用完全二叉树结论，利用数组存储的完全二叉树，其子结点和父结点的关系为~

  1. 前提：节点的父节点存在，且不为根节点。
  2. 设节点的下标为N
  3. 父节点下标 = (N-1)/2

思路分析

 由于是完全二叉树，因此我们需要层序遍历一遍，将完全二叉树转化为顺序结构，然后才可方便我们进行插入结点，那如何将完全二叉树转换为顺序结构呢？
 过程：先将根结点入对列，用0下标访问第一个节点，如果根结点不为空，则将其左节点和右节点再入对列，此时对列有三个结点，用下标访问下一个结点，即第二个节点，此时如果第二个节点不为空，则将其左右孩子再入对列，重复循环，直到访问到空节点为止。
  当需要添加节点时，我们只需要在遍历后，顺便记录一下，非空结点的个数，此时非空结点的个数即为添加节点的下标，再用上面的结论 计算父节点的下标，访问其父节点，并将此节点链接到父节点上即可。

队列与接口代码

typedef struct TreeNode TNode;
typedef struct Queue
{
    TNode** arr;
    int size;
    int capacity;
}Queue;

void QPushBack(Queue* que,TNode *val)
{
    if(que->capacity == que->size)
    {
        int capacity = que->capacity == 0 ? 4 : que->capacity * 2;
        TNode** tmp = (TNode**)realloc\
        (que->arr,sizeof(TNode*)*capacity);
        que->arr = tmp;
        que->capacity = capacity;
    }
    (que->arr)[que->size] = val;
    (que->size)++;
}
void Init(Queue* que)
{
    que->arr = NULL;
    que->size = 0;
    que->capacity = 0;
}
TNode* BuyNode(int v)
{
    TNode* NewNode = (TNode*)malloc(sizeof(TNode));
    NewNode->val = v;
    NewNode->left = NULL;
    NewNode->right = NULL;
    return NewNode;
}

题解代码

typedef struct 
{
    Queue que;
}CBTInserter;

CBTInserter* cBTInserterCreate(struct TreeNode* root) 
{
    CBTInserter* init = (CBTInserter*)malloc(sizeof(CBTInserter));
    Init(&(init->que));
    QPushBack(&(init->que),root);
    //插入根节点之后，进行层序遍历
    int sut = 0;//记录非空结点的个数
    while((init->que.arr)[sut]!=NULL)
    {
        TNode* cur = (init->que.arr)[sut];
        TNode* left = cur->left;
        TNode* right = cur->right;
        QPushBack(&(init->que),left);
        QPushBack(&(init->que),right);
        sut++;
    }
    init->que.size = sut;//记录非空结点的个数
    return init;
}

int cBTInserterInsert(CBTInserter* obj, int v)
{
    //初始化结点
    TNode* NewNode = BuyNode(v);
    int size = obj->que.size;//新节点的下标
    int pare = (size-1)/2;//父节点的下标
    TNode* pa = (obj->que.arr)[pare];//父节点
    if(pa->left == NULL)
    {
        pa->left = NewNode;
    } 
    else
    {
        pa->right = NewNode;
    }
    QPushBack(&(obj->que),NewNode);
    return pa->val;
}

struct TreeNode* cBTInserterGet_root(CBTInserter* obj)
{
    return (obj->que.arr)[0];
}

void cBTInserterFree(CBTInserter* obj) 
{
    free(obj->que.arr);
    free(obj);
}

四、二叉树每层的最大值

题目分析

在这里插入图片描述

思路分析

 此题要进行层序遍历，我们这里的应用非常灵活，先记录第一层的结点数，设为cur，进行出对列时，cur减减，看是否能更新当前一层的最大值，顺便把出队列结点的左右非空结点入队列，顺便记录一下此非空结点的个数，设为next，当cur减到0时，此时next就为下一层的非空结点个数，更新cur为next，next更新为0，顺便更新一下此层的max，对下一层的max进行初始化。cur与next循环更新，即为破题关键。

队列代码

typedef struct TreeNode TNode;
typedef struct QNode
{
    struct QNode* prev;
    struct QNode* next;
    TNode* val;
}QNode;
QNode* BuyNode(TNode*val)
{
    QNode* NewNode = (QNode*)malloc(sizeof(QNode));
    NewNode->val = val;
    NewNode->next = NULL;
    NewNode->prev = NULL;
    return NewNode;
}
void PushFront(QNode** head, TNode* val)
{
    QNode* New = BuyNode(val);
    QNode* Head = *head;
    if(Head == NULL)
    {
        New->next = New;
        New->prev = New; 
    }
    else
    {
        New->next = Head;
        New->prev = Head->prev;

        Head->prev->next = New;
        Head->prev = New; 
    }
    *head = New;
}
void PopBack(QNode**head)
{
    QNode* Head = *head;
    QNode* Tail = Head->prev;
    if(Tail == Head)
    {
        free(Tail);
        *head = NULL;
    }
    else
    {
        Head->prev = Tail->prev;
        Tail->prev->next = Head;
        free(Tail);
    }
}
bool is_empty(QNode** head)
{
    if(*head == NULL)
    {
        return true;
    }

    return false;
}

题解代码

int* largestValues(struct TreeNode* root, int* returnSize)
{
    int *arr = (int*)malloc(sizeof(int)*10000);
    int size = 0;
    int max = 0;
    QNode* head = NULL;
    int cur = 0;//当前层的个数
    int next = 0;//下一层的个数
    if(root!=NULL)
    {
        PushFront(&head,root);
        cur = 1;//第一层的个数
        max = root->val;
    }
    while(!is_empty(&head))
    {
        TNode* tail = head->prev->val;
        if(tail->val > max)
        {
            max = tail->val;
        }
        TNode* left = tail->left;
        TNode* right = tail->right;
        PopBack(&head);
        cur--;
        if(left != NULL)
        {
            PushFront(&head,left);
            next++;
        }
        if(right != NULL)
        {
            PushFront(&head,right);
            next++;
        }
        if(cur == 0)
        {
            //更新最大值
            arr[size++] = max;

            cur = next;
            next = 0;
            if(head!=NULL)
            {
                TNode* tail = head->prev->val;
                max = tail->val;
            }
        }
    }
    *returnSize = size;
    return arr;
}

下面的五、六题与第四题雷同。 对列代码也相同，下面就不给出了。

五、二叉树最底层最左边的值

题目分析

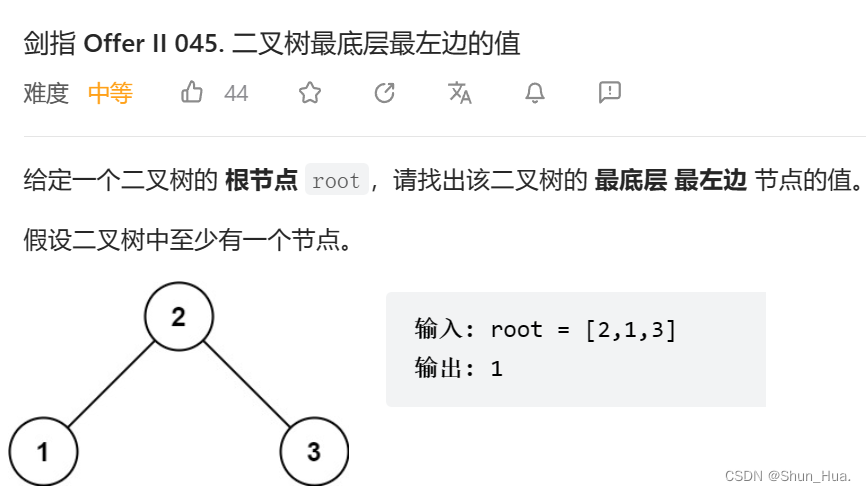
在这里插入图片描述

思路分析

思路与第四题，雷同，当进行换层时我们需要更新一下最左边的值，然后当next与cur都等于0时，此时保存的就是最左边的值。

代码

int findBottomLeftValue(struct TreeNode* root)
{
    QNode* head = NULL;
    PushFront(&head,root);
    int val_left = root->val;
    int cur = 1;
    int next = 0;
    while(!is_empty(&head))
    {
        TNode* Tail = head->prev->val;
        TNode* left = Tail->left;
        TNode* right = Tail->right;
        PopBack(&head);
        cur--;

        if(left != NULL)
        {
            PushFront(&head,left);
            next++;
        }
        if(right != NULL)
        {
            PushFront(&head,right);
            next++;
        }
        
        if(cur == 0)
        {
            if(next == 0)
            {
                //直接跳出循环即可。
                break;
            }

            cur = next;
            next = 0;
            if(head != NULL)
            {
                TNode* Tail = head->prev->val;
                val_left = Tail->val;
            }

        }
    }
    return val_left;
}

六、二叉树的右侧视图

题目分析

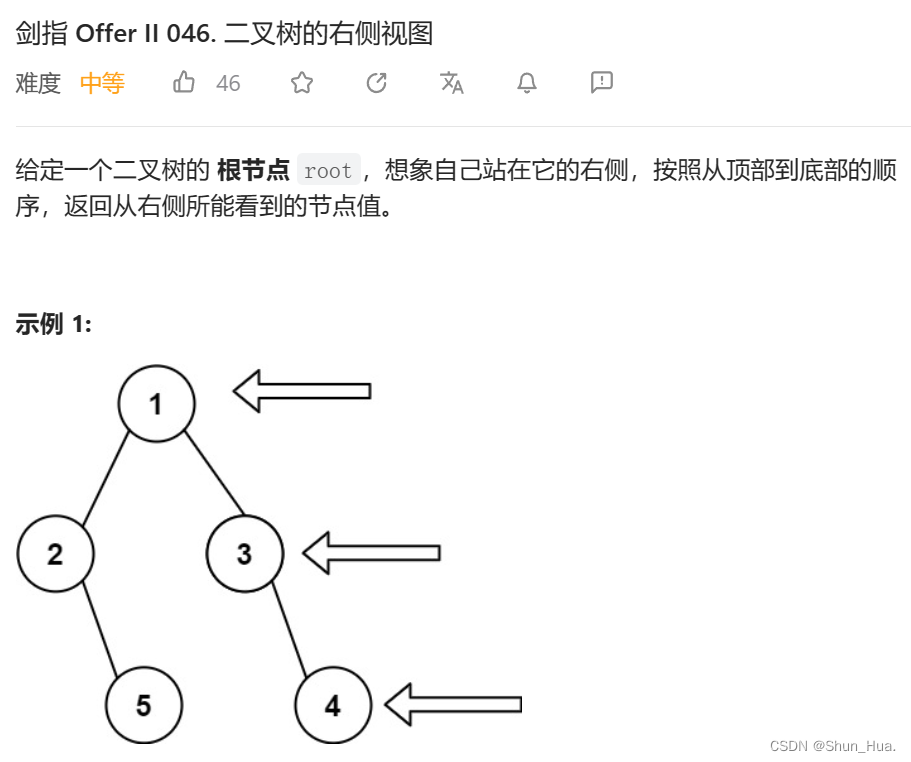
在这里插入图片描述

思路分析

 思路与第四题雷同，不过这里是，当cur等于0时，保存此层的最后一个结点的值。

代码

int* rightSideView(struct TreeNode* root, int* returnSize)
{
    QNode* head = NULL;

    int *arr = (int*)malloc(sizeof(int)*100);
    int size = 0;
    int cur = 0;
    int next = 0;
    if(root != NULL)
    {
        PushFront(&head,root);
        cur = 1;
    }
    while(!is_empty(&head))
    {
        TNode* Tail = head->prev->val;
        TNode* left = Tail->left;
        TNode* right = Tail->right;
        cur--;
        PopBack(&head);
        if(left != NULL)
        {
            PushFront(&head,left);
            next++;
        }
        if(right != NULL)
        {
            PushFront(&head,right);
            next++;
        }
        if(cur == 0)
        {
            arr[size++] = Tail->val;
            cur = next;
            next = 0;
        }
    }
    *returnSize = size;
    return arr;
}

总结

 今天的分享就到这里了，如果觉得文章不错，点个赞鼓励一下吧！我们下篇文章再见！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/671103.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

学习 WooCommerce REST API

学习 WooCommerce REST API

主要学习这个技术文档即可 WooCommerce REST API 技术文档 WooCommerce 官方文档 github : woocommerce/woocommerce 以下设置以及测试代码，都来自 WooCommerce REST API 技术文档 设置 REST API 设置 – 固定链接 （Settings > Permalinks.&#…
阅读更多...
MySQL - 第4节 - MySQL数据类型

MySQL - 第4节 - MySQL数据类型

目录 1.数据类型的作用 2.数据类型分类 3.数值类型 3.1.tinyint类型 3.2.bit类型 3.3.float类型 3.4.decimal类型 4.字符串类型 4.1.char类型 4.2.varchar类型 4.3.char和varchar比较 5.时间日期类型 6.enum和set类型 6.1.enum和set类型 6.2.调查表案例 6.3.通…
阅读更多...
二手车交易APP开发功能有哪些？

二手车交易APP开发功能有哪些？

二手车交易APP开发功能有哪些？ 1、车辆估价：在选购二手车时，了解车辆的市场价值是非常重要的。为了保证客户能够准确估计车辆的价值，二手车APP软件开发应该具备车辆估价功能。用户可以通过APP输入车辆的基本信息&#xff0…
阅读更多...
离线(内网)主机创建python项目运行环境

离线(内网)主机创建python项目运行环境

一、创建requirements.txt文件 文件中是python项目需要的依赖和版本号 二、把依赖下载到本地 准备一个能联网的pc，把依赖下载到本地 pip download -d ./venv -r requirements.txt -i https://pypi.mirrors.ustc.edu.cn/simple/这个命令会把依赖下载到venv文件夹…
阅读更多...
指数全线收跌，上证跌破3200点，仅4137只个股下跌！

指数全线收跌，上证跌破3200点，仅4137只个股下跌！

如题，端午假期前一天，A股指数全线收跌，上证指数跌破3200点，仅4137只个股下跌！就问你服不服？ 不要急，不要慌，我们来细细分析。 过去一两周，上证指数以震荡为主&#xff…
阅读更多...
嵌入式Linux学习入门

嵌入式Linux学习入门

大四毕业了，签了一份嵌入式开发的工作，现在准备入门了，搜集一些要学习的内容。 嵌入式开发学习路线 51单片机，arm，stm32在单片机上 在单片机上编程c语言和在嵌入式系统写c语言，有很大不同 gcc又与我们普…
阅读更多...
与反恐、反间谍科同级，美国国家安全部设立网络安全科

与反恐、反间谍科同级，美国国家安全部设立网络安全科

美国国家安全部（NSD）成立了一个新的网络部门，旨在能够更有力地应对高技术性的网络威胁。 这个新成立的部门，正式名称为国家网络安全科，是为了响应美国司法部 （DoJ） 2022 年全面网络审查中的核心…
阅读更多...
导致JVM内存泄露的ThreadLocal详解

导致JVM内存泄露的ThreadLocal详解

很常见的关于ThreadLocal的面试题的问法： 1.说说你对ThreadLocal的理解。 2.ThreadLocal 是什么？有哪 些使用场景？什么是线程局部变量？ 3.ThreadLocal内存泄漏分析与解决方案。 ps:想理解好ThreadLocal，必须先得理…
阅读更多...
Spring Boot命令行启动添加参数

Spring Boot命令行启动添加参数

一、Spring Boot命令行三种参数形式 通过java -jar启动springboot的jar项目时，可以动态传递参数来进行配置和开发，比如 java -jar xxx.jar --server.port8081 可以通过server.port修改项目启动的端口，通过命令行传递的参数具有更高的优先级…
阅读更多...
华为OD机试 JavaScript 实现【最优策略组合下的总的系统消耗资源数】【牛客练习题】，附详细解题思路

华为OD机试 JavaScript 实现【最优策略组合下的总的系统消耗资源数】【牛客练习题】，附详细解题思路

一、题目描述 在通信系统中有一个常见的问题是对用户进行不同策略的调度，会得到不同系统消耗的性能。 假设由N个待串行用户，每个用户可以使用A/B/C三种不同的调度策略，不同的策略会消耗不同的系统资源。 请你根据如下规则进行用户调度&…
阅读更多...
【Java-SpringBoot+Vue+MySql】Day3.2-RESTful风格

【Java-SpringBoot+Vue+MySql】Day3.2-RESTful风格

目录 一、RESTful风格介绍 1、知识轰炸 2、代码演练 （1）测试get接口 （2）测试Post接口 （3）测试Put接口 （4）测试delete接口 二、Swagger介绍 1、知识轰炸 2、实操演练 &#x…
阅读更多...
Android修行手册-多路USB外接摄像头

Android修行手册-多路USB外接摄像头

点击跳转>Unity3D特效百例点击跳转>案例项目实战源码点击跳转>游戏脚本-辅助自动化点击跳转>Android控件全解手册点击跳转>Scratch编程案例点击跳转>软考全系列 👉关于作者 专注于Android/Unity和各种游戏开发技巧，以及各种资源分享&…
阅读更多...
CSS3-盒子模型

CSS3-盒子模型

盒子模型的介绍 盒子概念 盒子组成 盒子内减 拓展 1. 盒子的概念 1 页面中的每一个标签，都可看做是一个 “盒子”，通过盒子的视角更方便的进行布局 2 浏览器在渲染（显示）网页时，会将网页中的元素看做是一个个的矩形区域…
阅读更多...
Selenium详解

Selenium详解

Selenium 环境配置好之后，我们就可以使用 Selenium 来操作浏览器，做一些我们想做的事情了。在我们爬取网页过程中，经常发现我们想要获得的数据并不能简单的通过解析 HTML 代码获取，这些数据是通过 AJAX 异步加载方式或经过 JS 渲染…
阅读更多...
Python高级系列教程：Python闭包和装饰器

Python高级系列教程：Python闭包和装饰器

今天我们将继续讲解 Python 中的闭包和装饰器。虽然我们还没有详细学习这两个概念，但在面向对象编程中，我们已经经常使用装饰器了。装饰器可以给函数增加额外的功能，就像语法糖一样甜。在 Python 中，装饰器的格式通常是在函数上方…
阅读更多...
三分钟学习一个python小知识1-----------我的对python的基本语法的理解

三分钟学习一个python小知识1-----------我的对python的基本语法的理解

文章目录 一、变量定义二、数据类型三、条件语句四、循环语句五、函数定义总结 一、变量定义 在Python中，使用等号（）进行变量的定义，并不需要声明变量的类型，Python会自动根据赋值的数据类型来判断变量的类型&#xf…
阅读更多...
算法篇——动态规划 完全和多重背包问题 (js版)

算法篇——动态规划 完全和多重背包问题 (js版)

一些分析总结 01 背包 问题和 完全背包 问题的不同点在于，所有的物品只能使用一次，判断 哪些物品 装进背包里 物品价值和 最大；而 完全背包 问题中，所有物品都能使用n次，判断 哪个物品 装 n 个进去 物品价值和 最大。…
阅读更多...
Mybatis源码分析_日志模块 （1）

Mybatis源码分析_日志模块 （1）

不得不承认，学习MyBatis的时间成本要比学习Spring低很多，Mybatis是我所了解过的代码量最小、整体架构最简单，但是又是最具有学习价值的一个框架。如果，你想快速的阅读一个框架的源码，并且掌握这个框架的精髓&#xff0…
阅读更多...
浅析GeoServer CVE-2023-25157 SQL注入

浅析GeoServer CVE-2023-25157 SQL注入

简介 GeoServer是一个开源的地图服务器&#xff0c;它是遵循OpenGIS Web服务器规范的J2EE实现&#xff0c;通过它可以方便的将地图数据发布为地图服务&#xff0c;实现地理空间数据在用户之间的共享。 影响版本 geoserver<2.18.7 2.19.0<geoserver<2.19.7 2.20.0…
阅读更多...
国内外八大敏捷开发工具盘点

国内外八大敏捷开发工具盘点

1、Leangoo领歌&#xff1b;官网&#xff1a;Leangoo领歌 - 高效企业必备的敏捷工具,Scrum工具,SAFe敏捷工具,敏捷项目管理,敏捷研发工具 2、VersionOne&#xff1b;官网&#xff1a;https://www.collab.net/products/versiononehttps://www.collab.net/products/versionone …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023