Leetcode
- Leetcode -617.合并二叉树
- Leetcode -1022.从根到叶的二进制数之和
Leetcode -617.合并二叉树
题目:给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意 : 合并过程必须从两个树的根节点开始。
示例 1:
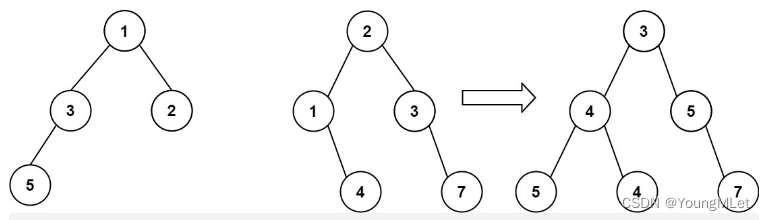
输入:root1 = [1, 3, 2, 5], root2 = [2, 1, 3, null, 4, null, 7]
输出:[3, 4, 5, 5, 4, null, 7]
示例 2:
输入:root1 = [1], root2 = [1, 2]
输出:[2, 2]
提示:
两棵树中的节点数目在范围[0, 2000] 内
- 10^4 <= Node.val <= 10^4
思路:化为子问题合并两棵树的根的左子树和右子树;结束条件为,如果其中一棵树的节点为空,就返回另外那棵树的节点;如果都不为空的情况,就 malloc 一个节点 newnode ,newnode 的 val 是当前两棵树的根的 val 的和,newnode 的 left 和 right 就继续分别递归两棵树的 left 和 right;
struct TreeNode* mergeTrees(struct TreeNode* root1, struct TreeNode* root2)
{
//如果 root1 为空,就返回 root2
if (!root1)
return root2;
//如果 root2 为空,就返回 root1
if (!root2)
return root1;
//都不为空的情况,malloc 一个节点,这个节点为 root1 和 root2 的 val 的和
struct TreeNode* newnode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
newnode->val = root1->val + root2->val;
//这个节点的左子树/右子树为 root1 与 root2 的左子树/右子树的合并,继续递归
newnode->left = mergeTrees(root1->left, root2->left);
newnode->right = mergeTrees(root1->right, root2->right);
//返回合并完的节点
return newnode;
}
Leetcode -1022.从根到叶的二进制数之和
题目:给出一棵二叉树,其上每个结点的值都是 0 或 1 。每一条从根到叶的路径都代表一个从最高有效位开始的二进制数。
例如,如果路径为 0 -> 1 -> 1 -> 0 -> 1,那么它表示二进制数 01101,也就是 13 。
对树上的每一片叶子,我们都要找出从根到该叶子的路径所表示的数字。
返回这些数字之和。题目数据保证答案是一个 32 位 整数。
示例 1:
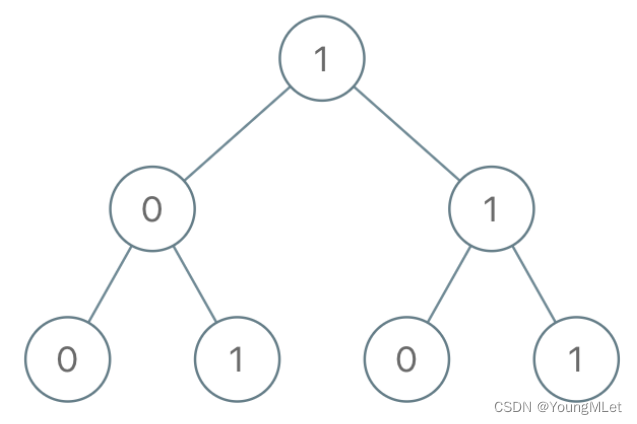
输入:root = [1, 0, 1, 0, 1, 0, 1]
输出:22
解释:(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22
示例 2:
输入:root = [0]
输出:0
提示:
树中的节点数在 [1, 1000] 范围内
Node.val 仅为 0 或 1
思路:化为子问题记录当前的 val ,把 val 递归当前根的左子树和右子树,返回左子树和右子树的二进制和;
int SumRoot(struct TreeNode* root, int val)
{
if (root == NULL)
return 0;
//val 向左移一位,按位或 root 的 val,得到 root 的 val
val = val << 1 | root->val;
//如果到叶子了,说明这条路径已经完了,返回这个二进制表示的数
if (root->left == NULL && root->right == NULL)
return val;
//每一次递归左子树和右子树之前,把当前的 val 递归进去,
//继续按位或它的左子树和右子树的 val,等待递归返回,
//就返回这个根的左子树和右子树的二进制和
return SumRoot(root->left, val) + SumRoot(root->right, val);
}
int sumRootToLeaf(struct TreeNode* root)
{
return SumRoot(root, 0);
}