之前好长一段时间都在写软著、写一些结课作业，就断断续续的在学，很少有时间把东西串起来，前些博文主要就是讲的说，做这个Z变换，今天就主要来看看其他的变换，当然，最重要的还是傅里叶变换，傅里叶变换到底是什么，我对书上的内容和看的几篇博客的内容总结了一下，大概意思就是说，现在有一个信号x(n)，我们已知的是，这个信号是由多个频率不同的信号叠加形成的，但是我们没有办法在时间域对他们进行分离，那怎么办呢，频域给我们提供了思路，因为我们知道的是这个合成信号各个组分的频率是不同的，那么在频域就能够很简单的将各个组分进行区分，当然，这只是我个人的简单理解，要深究的话，还是得回归课本，比如我在第一篇就提到的绿皮书，我感觉这本书应该是数字信号处理的集大成了，还有，我找了一篇博客，这个博主讲的很细致，也很通透，可以看一看：https://blog.csdn.net/qq_37568748/article/details/80402313?ops_request_misc=&request_id=&biz_id=102&utm_term=%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-2-80402313.142^v88^control_2,239^v2^insert_chatgpt&spm=1018.2226.3001.4187

简单的来看一个例子：现在，我们有一个由多个信号合成的信号：

from matplotlib import pyplot as plt 
from scipy import signal,fft,fftpack
import numpy as np
import cmath
import random
#这里展现的是个连续信号
n=np.linspace(-10,10,10000,dtype=float)
x1=np.cos(0.9*np.pi*n)
x2=np.sin(0.5*np.pi*n)
x3=np.cos(0.4*np.pi*n)
X=0.1*x1+0.2*x2+0.3*x3+random.randint(1,4)
figure=plt.figure(figsize=(15,15))
ax1=figure.add_subplot(2,3,1)
ax1.plot(X)
F=np.fft.fft(X)
ax2=figure.add_subplot(2,3,2)
ax2.plot(F)
ax3=figure.add_subplot(2,3,3)
ax3.plot(F.real)
ax4=figure.add_subplot(2,3,4)
ax4.plot(F.imag)
ax5=figure.add_subplot(2,3,5)
ax5.plot(F.real[0:15])
ax6=figure.add_subplot(2,3,6)
ax6.plot(F.real[9985:10000])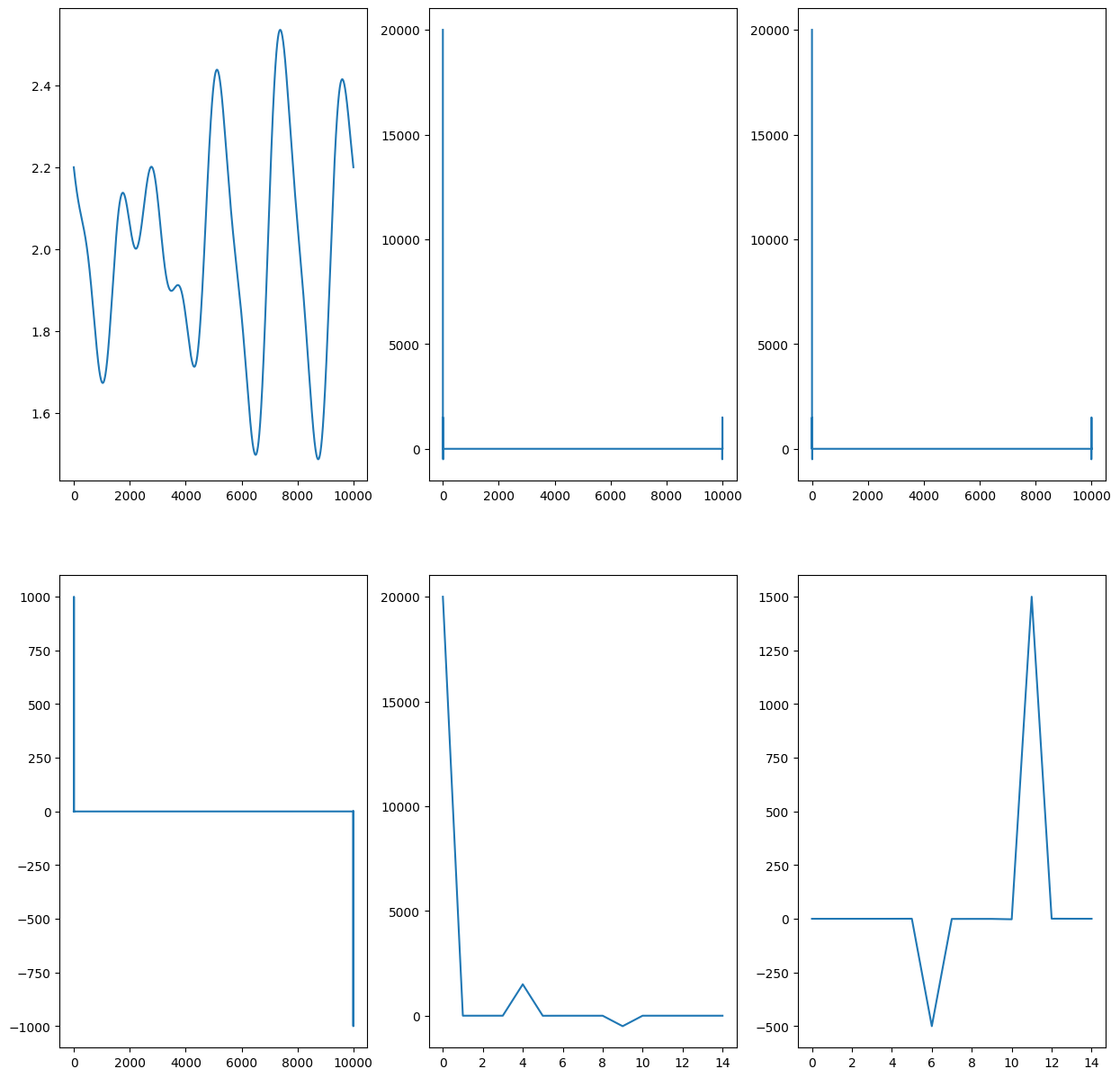

 傅里叶变换的性质，我就不多说什么了，在这讲公式还不如看看实际的。

对了，Python的好几个包都是由fft的，现在，以我来说用的多有：

假设我们现在有一个信号X(n)
#1、numpy的fft模块
import numpy as np
XFFT=np.fft.fft(x)
#逆变换
IXFFT=np.fft.ifft(XFFT)
2、scipy的fftpack模块
from scipy import fftpack
XFFT=fftpack.fft(x)
#逆变换
IXFFT=fftpack.ifft(XFFT)
3、scipy的fft模块
from scipy import fft
XFFT=fft.fft(x)
#逆变换
IXFFT=fft.ifft(XFFT)

他们的功能都是一模一样的，同时，也都有卷积功能，很方便。

 重点就来说说快速傅里叶变换，这是用的最多的，他有很多算法，比如说：基2时分、基2频分，甚至说基4xx，说实话，我看完讲解就感觉他的工作内容就是二分法，或者更简单一些就是我们学算法的时候说的那个分而治之思想。

我们来看一个一个叠加信号经过快速傅里叶变换之后的频谱图：

import numpy as np
from scipy import signal,fftpack
from matplotlib import pyplot as plt
#已知信号是x=0.5sin(2pi*20*t)+2sin(2pi*60*t),f1=20Hz,f2=60Hz,采样频率是100Hz，展现经过快速傅里叶变换之后的频谱图
fs=100
Ndata=32
Ndata2=136
N2=32
N2=128
N3=512
n=np.linspace(0,Ndata-1,Ndata,dtype=int)
t=n/fs
x=0.5*np.sin(2*np.pi*20*t)+2*np.sin(2*np.pi*60*t)
y=fftpack.fft(x,n=N2)
mag=np.abs(y)
f=np.linspace(0,N2-1,N2,dtype=int)*fs/N2
figure1=plt.figure(figsize=(15, 15))
ax1=figure1.add_subplot(2,2,1)
ax1.plot(f[:int(N2/2)],mag[:int(N2/2)]*2/N2)
ax1.set_xlabel('frequence/Hz')
ax1.set_ylabel('Amplitude')
ax1.set_title("Ndata=32,FFT's sample number=32")
f2=np.linspace(0,N2-1,N2,dtype=int)*fs/N2
y2=fftpack.fft(x,N2)
mag2=np.abs(y2)
ax2=figure1.add_subplot(2,2,2)
ax2.plot(f2[:int(N2/2)],mag2[:int(N2/2)]*2/N2)
ax2.set_xlabel('frequence/Hz')
ax2.set_ylabel('Amplitude')
ax2.set_title("Ndata=32,FFT's sample number=128")
n2=np.linspace(0,Ndata2-1,Ndata2,dtype=int)
t2=n2/fs
x2=0.5*np.sin(2*np.pi*20*t2)+2*np.sin(2*np.pi*60*t2)
y3=fftpack.fft(x2,N2)
mag3=np.abs(y3)
f3=np.linspace(0,N2-1,N2,dtype=int)*fs/N2
ax3=figure1.add_subplot(2,2,3)
ax3.plot(f3[:int(N2/2)],mag3[:int(N2/2)]*2/N2)
ax3.set_xlabel('frequence/Hz')
ax3.set_ylabel('Amplitude')
ax3.set_title("Ndata=136,FFT's sample number=128")
n3=np.linspace(0,Ndata2-1,Ndata2,dtype=int)
t3=n3/fs
x3=0.5*np.sin(2*np.pi*20*t3)+2*np.sin(2*np.pi*60*t3)
y4=fftpack.fft(x3,N3)
mag4=np.abs(y4)
f4=np.linspace(0,N3-1,N3,dtype=int)*fs/N3
ax4=figure1.add_subplot(2,2,4)
ax4.plot(f4[:int(N3/2)],mag4[:int(N3/2)]*2/N3)
ax4.set_xlabel('frequence/Hz')
ax4.set_ylabel('Amplitude')
ax4.set_title("Ndata=136,FFT's sample number=512")
ax1.grid(visible=True)
ax2.grid(visible=True)
ax3.grid(visible=True)
ax4.grid(visible=True)
plt.rcParams['figure.figsize']=(12.8, 7.2)
plt.show()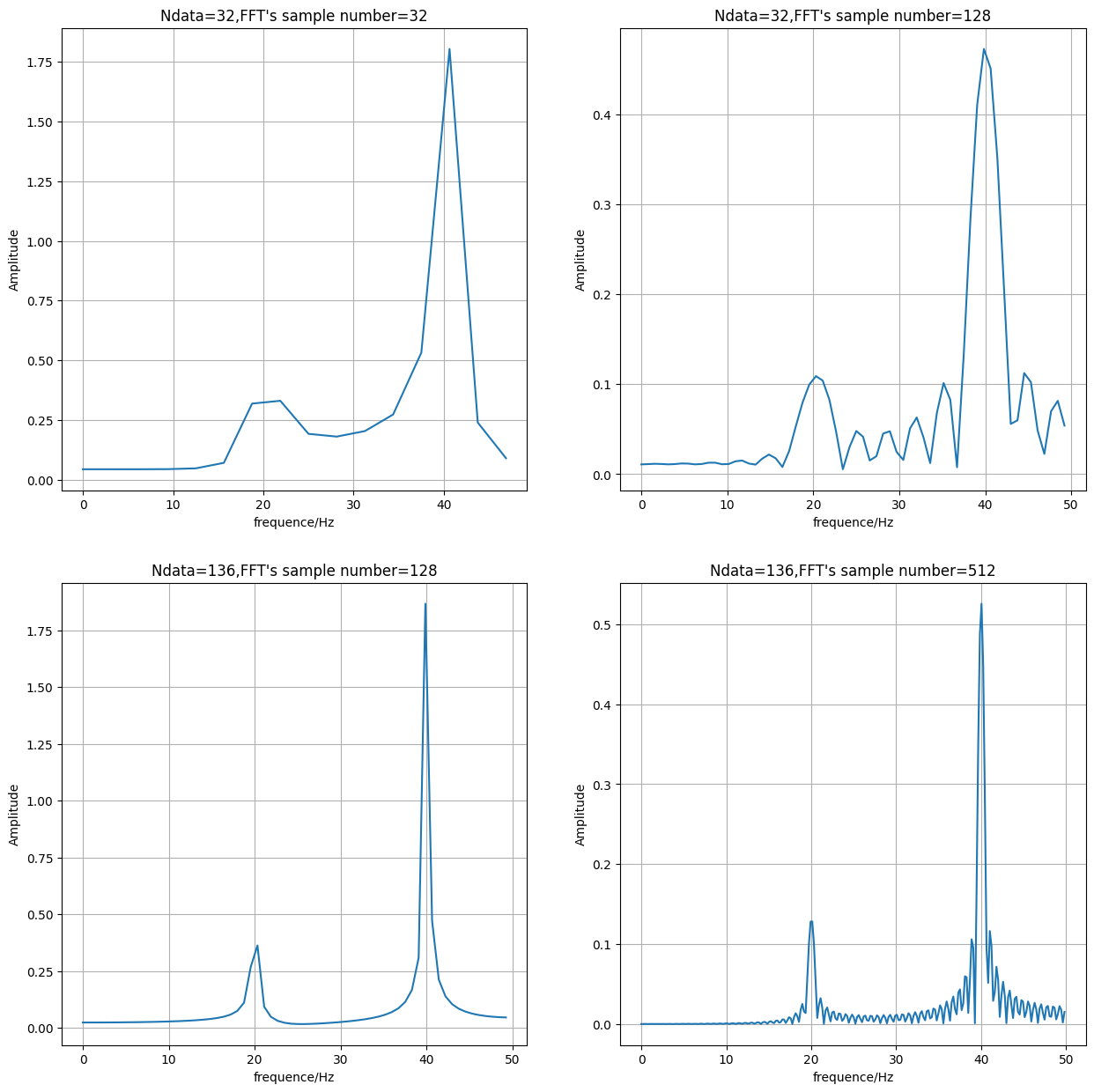

 再来看一个频谱分析的例子：

import numpy as np
from scipy import signal,fftpack
from matplotlib import pyplot as plt
import random
#对一个正弦信号、一个余弦信号、白噪声的叠加信号X(n)做频谱分析
N2=1024
f1=0.1
f2=0.2
fs=1
a1=5
a2=3
w=2*np.pi/fs
x=a1*np.sin(w*f1*np.linspace(0,N2-1,N2,dtype=int))+a2*np.cos(w*f2*np.linspace(0,N2-1,N2,dtype=int))+random.randint(1,N2)
#用FFT求频谱
fig=plt.figure(figsize=(10,10))
ax1=fig.add_subplot(2,1,1)
ax1.plot(x[0:int(N2/4)])
ax1.set_title("Original Signal")
f=np.linspace(-0.5,0.5,N2,dtype=float)
X=fftpack.fft(x,N2)
ax2=fig.add_subplot(2,1,2)
ax2.plot(f,fftpack.fftshift(np.abs(X)))
ax2.axis([-0.5,0.5,0,2000])
ax2.set_title('frequency signal')
ax1.grid(visible=True)
ax2.grid(visible=True)
plt.show()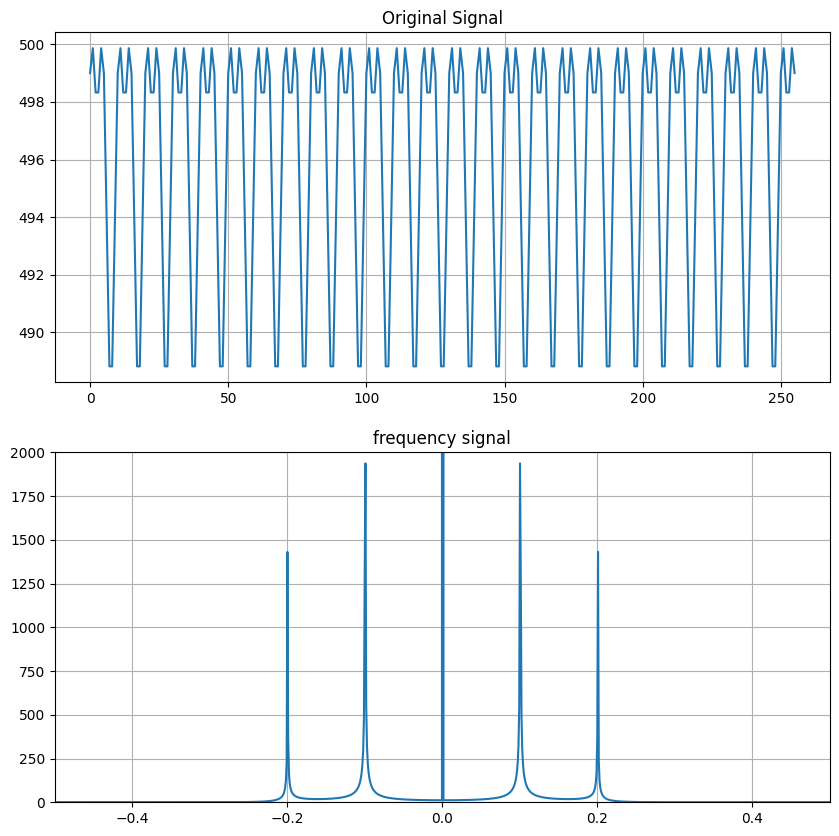

傅里叶逆变换：你不能老是让信号再频率域呆着，返回时域我们才能更好的分析，那么怎么回到时域呢，直接使用逆变换就好：

#逆FFT
import numpy as np
from scipy import signal,fftpack
from matplotlib import pyplot as plt
fs=200
N2=128
n=np.linspace(0,N2-1,N2,dtype=int)
t=n/fs
x=0.5*np.sin(2*np.pi*20*t)+2*np.sin(2*np.pi*60*t)
fig2=plt.figure(figsize=(12,12))
ax1=fig2.add_subplot(2,2,1)
ax1.plot(t,x)
ax1.set_xlabel('time/s')
ax1.set_ylabel('x')
ax1.set_title("Original Signal")
ax1.grid(visible=True)
y=fftpack.fft(x)
mag=np.abs(y)
f=n*fs/N2
ax2=fig2.add_subplot(2,2,2)
ax2.plot(f[:int(N2/2)],mag[:int(N2/2)]*2/N2)
ax2.set_xlabel('frequency/Hz')
ax2.set_ylabel('x')
ax2.set_title("Original Signal's FFT")
ax2.grid(visible=True)
xifft=fftpack.ifft(y)
realx=xifft.real
ti=np.linspace(0,len(xifft)-1,len(xifft),dtype=float)/fs
ax3=fig2.add_subplot(2,2,3)
ax3.plot(ti,realx)
ax3.set_xlabel('time/s')
ax3.set_ylabel('x')
ax3.set_title("using IFFT ")
ax3.grid(visible=True)
yif=fftpack.fft(xifft)
mag2=np.abs(yif)
f2=np.linspace(0,len(y)-1,len(y),dtype=float)*fs/len(y)
ax4=fig2.add_subplot(2,2,4)
ax4.plot(f2[:int(N2/2)],mag2[:int(N2/2)]*2/N2)
ax4.set_xlabel('frequence/Hz')
ax4.set_ylabel('Amplitude')
ax4.set_title("Using Ifft gain the FFT of the Signal")
ax4.grid(visible=True)
ax4.grid(visible=True)
ax1.axis([0,1,-2.5,2.5])
ax3.axis([0,1,-2.5,2.5])
plt.show()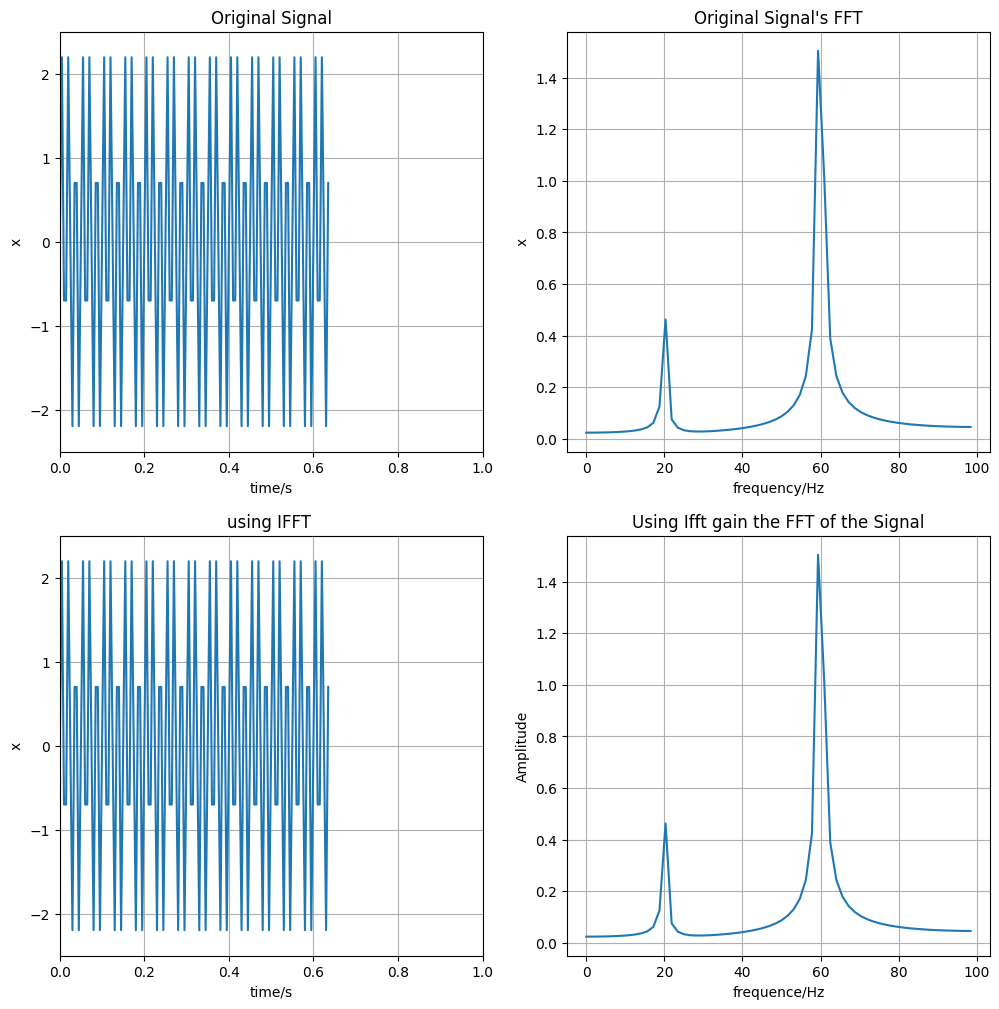

 说白了，我们要傅里叶变换和逆变换干啥呢，不就是供后期滤波嘛，所以，接下来看一个用傅里叶变换变换到频域，滤波后再用逆变换返回时域的例子，在这我贴个我做的一个很简单的例子，实际上，我对我的这个信号进行了高斯滤波，来看一下：

原始信号：

 

 

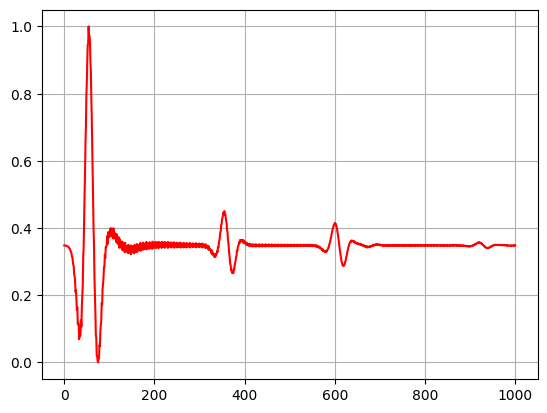
滤波后的信号：

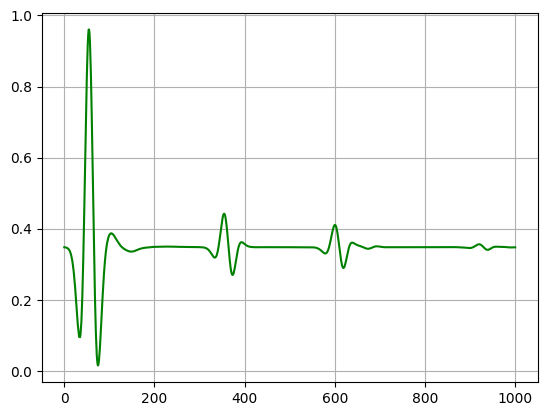
原始和滤波后的信号变换至频域：

1、实部：

红色为滤波后：

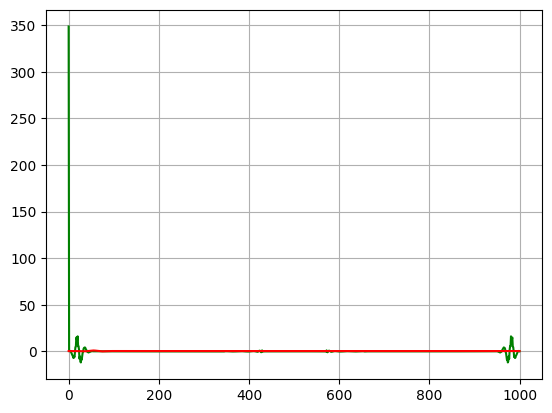
 但是啊，滤波后的信号实部不为零：

2、虚部： 

绿色为原始信号虚部：

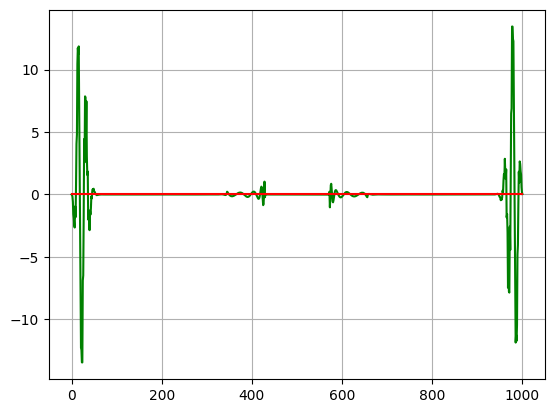
 滤波后的信号虚部：

 这里主要就是体现一下滤波操作，完整的代码如下：

import numpy as np
import matplotlib.pyplot as plt
import cv2
from math import ceil
d=np.genfromtxt("I:\Read\Signal\sig.data")
G=cv2.GaussianBlur(d,ksize=(ceil(2*3)+1,ceil(2*3)+1),sigmaX=3,sigmaY=3)
fftd=np.fft.fft(d)
fftG=np.fft.fft(G)
plt.figure()
plt.plot(fftd.imag,'g')
plt.plot(fftG.imag,'r')
plt.grid(True)
plt.figure()
plt.plot(fftd.real,'g')
plt.plot(fftG.real,'r')
plt.grid(True)
plt.figure()
plt.grid(True)
plt.plot(G,'g')
plt.figure()
plt.grid(True)
plt.plot(d,'r')
plt.figure()
plt.plot(fftG.real)
plt.figure()
plt.plot(fftG.imag)

注意，我在这里用了OpenCv的高斯滤波来去除原始信号里的随机噪声。

离散余弦变换，只要你学过傅里叶级数就能知道，这个离散余弦变换就是FFT的特殊情况：展开式中，被展开的函数是实偶函数，傅里叶级数只包含余弦项，离散化后就导出了余弦变换：

这里我们使用fft的dct函数就行，MATLAB里也有dct：

# distribution COS Transforms
import numpy as np
from scipy import signal,fftpack,fft
from matplotlib import pyplot as plt
n=np.linspace(1,100,100,dtype=int)
x=10*np.sin(2*np.pi*n/20)+20*np.cos(2*np.pi*n/30)
y=fft.dct(x)
fig4=plt.figure(figsize=(20,8))
ax1=fig4.add_subplot(1,2,1)
ax1.plot(x)
ax1.set_title("Original Signal")
ax2=fig4.add_subplot(1,2,2)
ax2.plot(y)
ax2.set_title("Dct")
plt.show()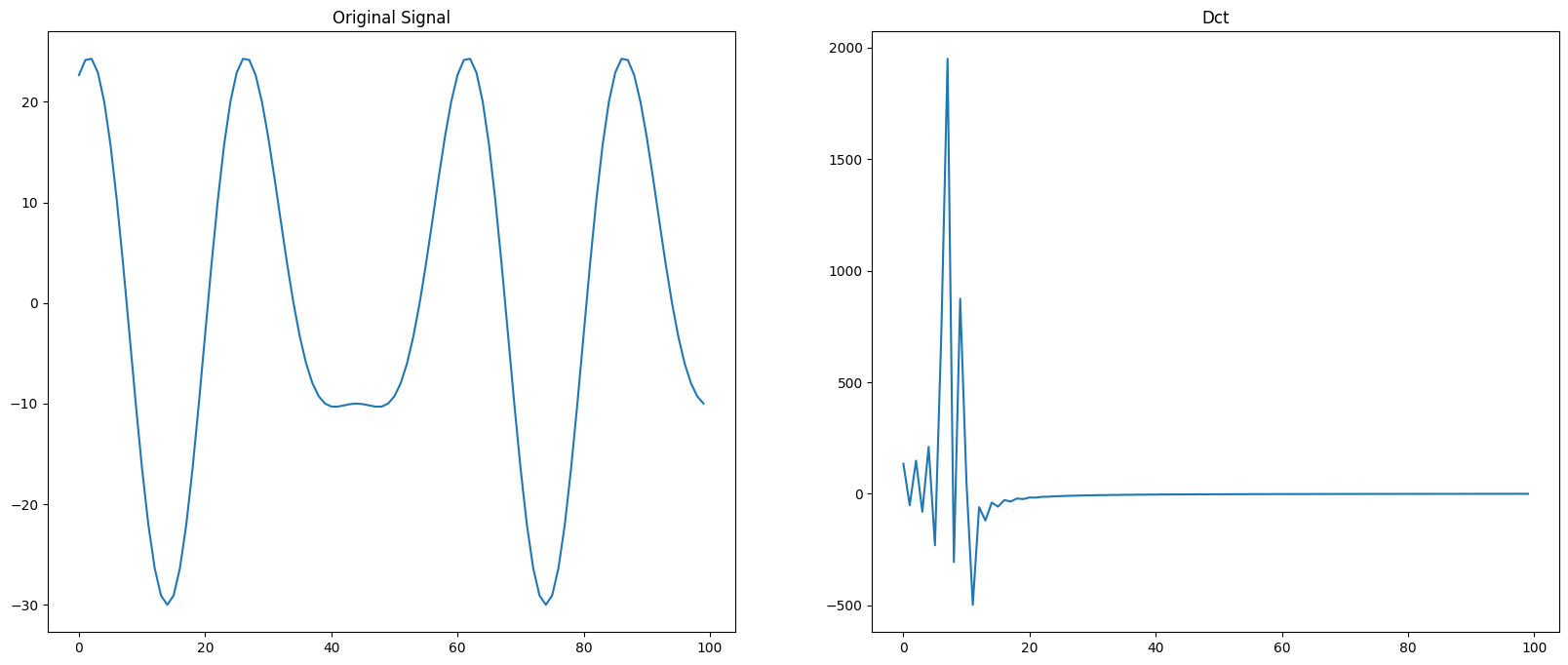

 来看看逆变换，这个有点问题，我的图和书上的还不太一样：

# Invert distribution COS Transforms
import numpy as np
from scipy import signal,fftpack,fft
from matplotlib import pyplot as plt
n=np.linspace(0,199,200,dtype=int)
f=200
fs=3000
x=np.cos(2*np.pi*n*f/fs)
y=fft.dct(x)
G=np.abs(y)
m=[]
for i in range(f):
    if G[i]<5:
        m.append(i)
for i in range(len(m)):
    y[m[i]]=0
z=fft.idct(y)
figure4=plt.figure(figsize=(20,8))
ax1=figure4.add_subplot(1,2,1)
ax1.plot(n,x)
ax1.set_xlabel("n")
ax1.set_title("Sequence x(n)")
ax2=figure4.add_subplot(1,2,2)
ax2.plot(n,z)
ax2.set_title("Sequence z(n)")
ax2.set_xlabel("n")
ax1.grid(True)
ax2.grid(True)
plt.show()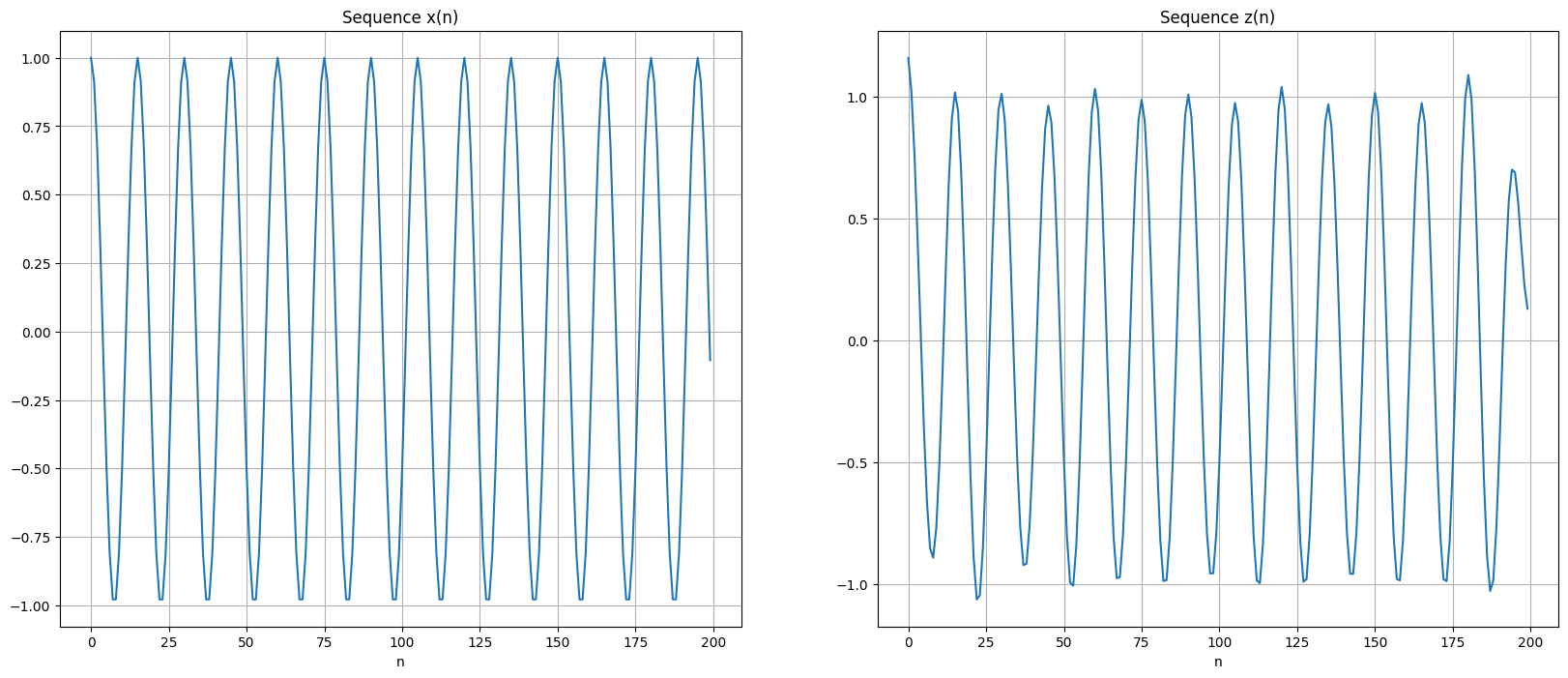

 最后我们来看看ChirpZ变换，czt函数就好：

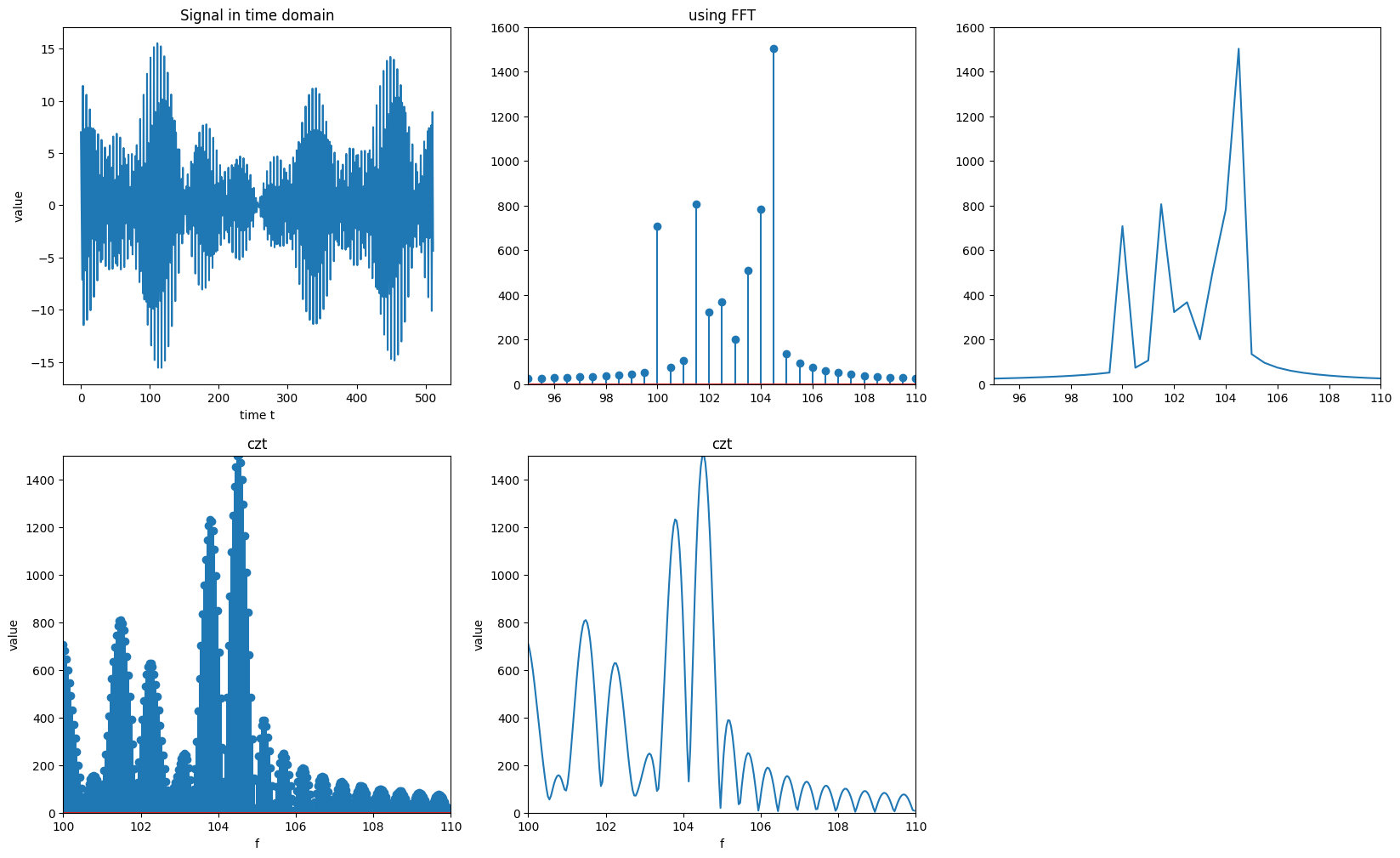
来看看使用CZT函数实现频率细化的例子：

#利用CZT函数实现频率细化
import numpy as np
from scipy import signal,fftpack,fft
from matplotlib import pyplot as plt
import cmath
fs=256
N=512
nfft=512
n=np.linspace(0,N-1,N,dtype=int)
I1=np.linspace(0,int(nfft/2)-1,int(nfft/2),dtype=int)
n1=fs*I1/nfft
x=3*np.sin(2*np.pi*100*n/fs)+3*np.cos(2*np.pi*101.45*n/fs)+2*np.sin(2*np.pi*102.3*n/fs)+4*np.cos(2*np.pi*103.8*n/fs)+5*np.sin(2*np.pi*104.5*n/fs)
figure=plt.figure(figsize=(20,12))
ax1=figure.add_subplot(2,3,1)
ax1.plot(n,x)
ax1.set_xlabel("time t")
ax1.set_ylabel("value")
ax1.set_title("Signal in time domain")
XX=np.fft.fft(x,nfft)
ax2=figure.add_subplot(2,3,2)
ax2.stem(n1,np.abs(XX[:int(nfft/2)]))
ax2.set_title("using FFT")
ax2.axis([95,110,0,1600])
ax3=figure.add_subplot(2,3,3)
ax3.plot(n1,np.abs(XX[:int(N/2)]))
ax3.axis([95,110,0,1600])
f1=100
f2=110
M=256
w=np.exp(-cmath.sqrt(-1)*2*np.pi*(f2-f1)/(fs*M))
a=np.exp(cmath.sqrt(-1)*2*np.pi*f1/fs)
xk=signal.czt(x,M,w,a)
h=np.linspace(0,M-1,M,dtype=int)
f0=(f2-f1)/M*h+100
ax4=figure.add_subplot(2,3,4)
ax4.stem(f0,np.abs(xk))
ax4.set_xlabel("f")
ax4.set_ylabel("value")
ax4.set_title("czt")
ax4.axis([100,110,0,1500])
ax5=figure.add_subplot(2,3,5)
ax5.plot(f0,np.abs(xk))
ax5.set_xlabel("f")
ax5.set_ylabel("value")
ax5.set_title("czt")
ax5.axis([100,110,0,1500])
plt.show()

 好了，大致就这样吧，还用很多我都还没学，学到哪算哪吧