Day40——Dp专题

文章目录

- 三、01背包
- - 8.分割等和子集
  - 9.最后一块石头的重量 II
  - 10.目标和
  - 11. 一和零

三、01背包

8.分割等和子集

题目链接：416. 分割等和子集 - 力扣（LeetCode）

思路：我们构造两个子集使得两个子集的和相等，其实就是让我们构造其中一个子集的和是否等于sum / 2，若存在说明能分割等和子集。如果sum为奇数，是不能分割等和子集的。

换句话说，题目就是让我们从nums[]中选择一些物品，使得物品的总和恰好为target(sum / 2)，为此可以转化为01背包问题

递归五部曲

确定dp数组以及下标含义

dp[j]表示背包总容量（所能装的总重量）是j，放进物品后，背的最大重量为dp[j]

确定递推公式

01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

本题，相当于背包里放入数值，那么物品i的重量是nums[i]，其价值也是nums[i]。

所以递推公式：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);

dp数组初始化

从dp[j]的定义来看，首先dp[0]一定是0，这样才能让dp数组在递归公式的过程中取的最大的价值，而不是被初始值覆盖了

确定遍历顺序

如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！

打印举例dp数组

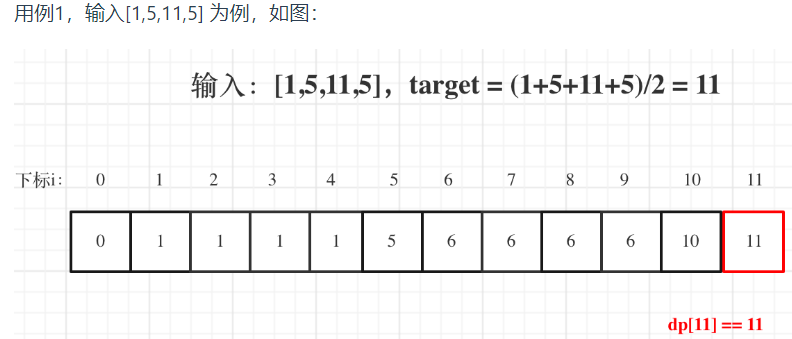
Code

一维

class Solution {
    public boolean canPartition(int[] nums) {
        if(nums == null || nums.length == 0) return false;
        int n = nums.length;
        int sum = 0;
        for(int num : nums){
            sum += num;
        }

        if(sum % 2 != 0) return false;
        int target = sum/2;
        int[] dp = new int[target+1];
        for(int i = 0; i < n; i++){
            for(int j = target; j >= nums[i]; j--){
                dp[j] = Math.max(dp[j],dp[j-nums[i]] + nums[i]);
            }
        }
        return dp[target] == target;
    }
}

二维

class Solution {
    public boolean canPartition(int[] nums) {
        int sum = 0;
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
        }

        if (sum % 2 == 1)
            return false;
        int target = sum / 2;

        //dp[i][j]代表可装物品为0-i，背包容量为j的情况下，背包内容量的最大价值
        int[][] dp = new int[nums.length][target + 1];

        //初始化,dp[0][j]的最大价值nums[0](if j > weight[i])
        //dp[i][0]均为0，不用初始化
        for (int j = nums[0]; j <= target; j++) {
            dp[0][j] = nums[0];
        }

        //遍历物品，遍历背包
        //递推公式:
        for (int i = 1; i < nums.length; i++) {
            for (int j = 0; j <= target; j++) {
                //背包容量可以容纳nums[i]
                if (j >= nums[i]) {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }

        return dp[nums.length - 1][target] == target;
    }
}

9.最后一块石头的重量 II

题目链接：1049. 最后一块石头的重量 II - 力扣（LeetCode）

思路：两个两个集合总和越平均越好，即尽量接近于各占一半

状态计算：f[j] = max(f[j], f[j - stones[i]] + stones[i])

最后一块石头的的最小重量：sum - 2 * f[half]

动规五部曲：

确定dp数组以及下标的含义

dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背最大重量为dp[j]

相对于 01背包，本题中，石头的重量是 stones[i]，石头的价值也是 stones[i] ，可以 “最多可以装的价值为 dp[j]” == “最多可以背的重量为dp[j]”

确定递推公式

本题中 f[j] = max(f[j], f[j - stones[i]] + stones[i])

dp数组初始化

dp[j]都初始化为0就可以了，这样在递归公式dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);中dp[j]才不会初始值所覆盖，dp数组的大小为target = sum/2 + 1

确定遍历顺序

如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！

打印并举例dp数组

最后dp[target]里是容量为target的背包所能背的最大重量。

那么分成两堆石头，一堆石头的总重量是dp[target]，另一堆就是sum - dp[target]。

在计算target的时候，target = sum / 2 因为是向下取整，所以sum - dp[target] 一定是大于等于dp[target]的。

那么相撞之后剩下的最小石头重量就是 (sum - dp[target]) - dp[target]。

Code

一维

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int sum = 0;
        int n = stones.length;
        for(int i : stones){
            sum += i;
        }
        int target = sum >> 1;
        int[] dp = new int [target+1];
        for(int i = 0; i < n; i++){
            for(int j = target; j >= stones[i]; j--){
                dp[j] = Math.max(dp[j],dp[j - stones[i]] + stones[i]);
            }
        }
        return sum - 2*dp[target];
    }
}

二维

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int sum = 0;
        for (int s : stones) {
            sum += s;
        }

        int target = sum / 2;
        //初始化，dp[i][j]为可以放0-i物品，背包容量为j的情况下背包中的最大价值
        int[][] dp = new int[stones.length][target + 1];
        //dp[i][0]默认初始化为0
        //dp[0][j]取决于stones[0]
        for (int j = stones[0]; j <= target; j++) {
            dp[0][j] = stones[0];
        }

        for (int i = 1; i < stones.length; i++) {
            for (int j = 1; j <= target; j++) {//注意是等于
                if (j >= stones[i]) {
                    //不放:dp[i - 1][j] 放:dp[i - 1][j - stones[i]] + stones[i]
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - stones[i]] + stones[i]);
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        System.out.println(dp[stones.length - 1][target]);
        return (sum - dp[stones.length - 1][target]) - dp[stones.length - 1][target];
    }
}

10.目标和

题目链接：力扣题目链接

思路：每个数前面加+ 或者 -可以联想01背包，要么0要么1我们将数组分为两部分，一部分为正数的p，一部分为负数的ne，

我们想要sum(p) + sum(ne) == S，而数组的和是已知的即sum(p) + sum(ne) == sum

两式相加化简得sum(p) = (sum + S) / 2 = targrt，也就是说我们要从nums[]里边选几个数使其和为target，

于是就转换为求容量恰好为taeget的01背包问题。

确定dp数组以及下标的含义

dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法

确定递推公式

例如：dp[j]，j 为5，

已经有一个1（nums[i]）的话，有 dp[4]种方法凑成容量为5的背包。
已经有一个2（nums[i]）的话，有 dp[3]种方法凑成容量为5的背包。
已经有一个3（nums[i]）的话，有 dp[2]中方法凑成容量为5的背包
已经有一个4（nums[i]）的话，有 dp[1]中方法凑成容量为5的背包
已经有一个5 （nums[i]）的话，有 dp[0]中方法凑成容量为5的背包

那么凑整dp[5]有多少方法呢，也就是把所有的 dp[j - nums[i]] 累加起来。

dp[j] += dp[j-nums[i]];

dp数组初始化

f[0] = 1，体积为0（和为0），那就是一个物品都不放，有一种方案。

确定遍历顺序

nums放在外循环，target在内循环，且内循环倒序。

 for(int i = 0; i < nums.length ;i++){
            for(int j = size; j >= nums[i]; j--){
                dp[j] += dp[j-nums[i]];
            }
        }

举例推导dp数组

输入：nums: [1, 1, 1, 1, 1], S: 3

bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4

dp数组状态变化如下：

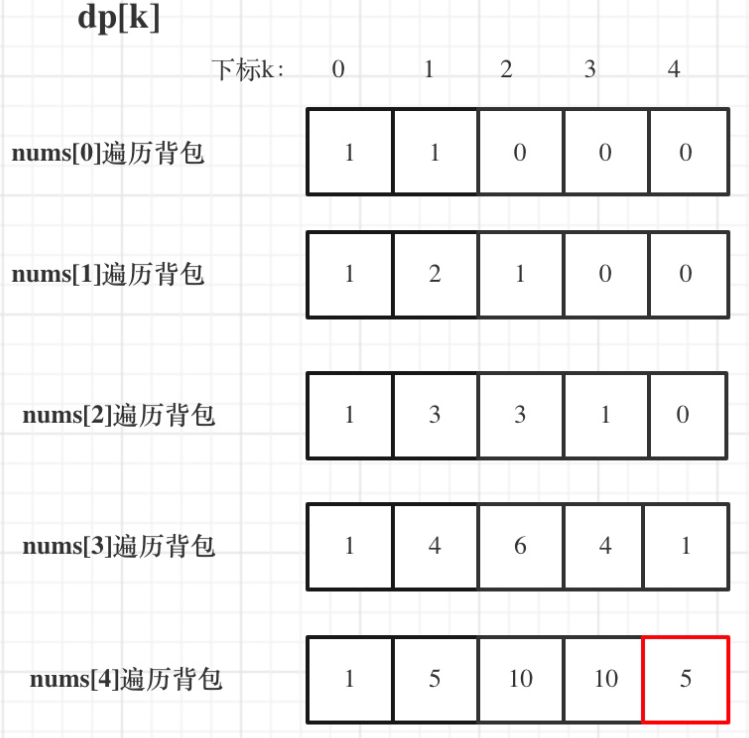
Code

一维

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum  = 0;
        for(int i : nums){
            sum += i;
        }
        int size = (target + sum) >> 1;
        if(target > sum || target < -sum || (target + sum) % 2 == 1){
            return 0;
        }
        int[] dp = new int[size + 1];
        dp[0] = 1;
        for(int i = 0; i < nums.length ;i++){
            for(int j = size; j >= nums[i]; j--){
                dp[j] += dp[j-nums[i]];
            }
        }
        return dp[size];
    }
}

11. 一和零

题目链接：474. 一和零 - 力扣（LeetCode）

动规五部曲

确定dp数组以及下标的含义

dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。

确定递推公式

trs里的字符串有zeroNum个0，oneNum个1。

dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。

然后我们在遍历的过程中，取dp[i][j]的最大值。

所以递推公式：dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

dp数组初始化

1背包的dp数组初始化为0就可以。

因为物品价值不会是负数，初始为0，保证递推的时候dp[i][j]不会被初始值覆盖

确定遍历顺序

for循环遍历物品，内层for循环遍历背包容量且从后向前遍历

举例推导dp数组

Code

二维

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int[][] dp = new int[m+1][n+1];
        int oneNum,zeroNum;
        for(String str : strs){
            oneNum = 0;
            zeroNum = 0;
            for(char ch : str.toCharArray()){
                if(ch=='0'){
                   zeroNum++; 
                }else{
                    oneNum++;
                }
            }
            //倒叙遍历
            for(int i = m; i >= zeroNum; i--){
                for(int j = n; j>=oneNum; j--){
                    dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum]+1);
                }
            }
        }
        return dp[m][n];
    }
}