目录

题目描述

输入描述

输出描述

用例

题目解析

算法源码

---

题目描述

给一个无向图染色，可以填红黑两种颜色，必须保证相邻两个节点不能同时为红色，输出有多少种不同的染色方案？

输入描述

第一行输入M(图中节点数) N(边数)

后续N行格式为：V1 V2表示一个V1到V2的边。

数据范围：1 <= M <= 15,0 <= N <= M * 3，不能保证所有节点都是连通的。

输出描述

输出一个数字表示染色方案的个数。

用例

输入	4 4 1 2 2 4 3 4 1 3
输出	7
说明	4个节点，4条边，1号节点和2号节点相连， 2号节点和4号节点相连，3号节点和4号节点相连， 1号节点和3号节点相连， 若想必须保证相邻两个节点不能同时为红色，总共7种方案。

题目解析

用例的染色方案，如下示意图：

相邻节点不能同时为红色

求一个连通图的染色方案，策略如下：
首先，必然有一种全黑方案。

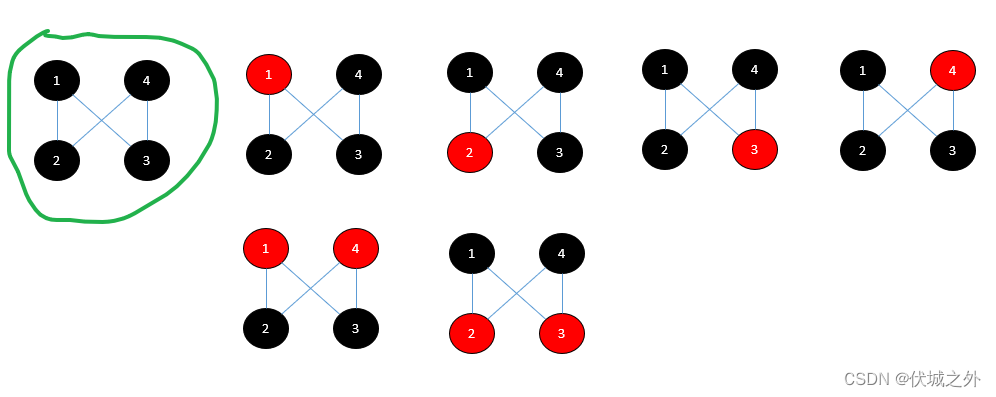
 然后，我们找第一个点，即点1，找它的不相邻点，只有一个4，因此我们可以选择只给1染色，或者只给4染色，或者给1，4同时染色，这三个方案都符合要求

其实，这就是求1，4的全组合个数，即求 C(n,1) + C(n,2) + C(n,3) + ...... + C(n,n-1) + C(n,n) = (2^n) - 1

比如1，4有两个数，即一共有 (2^2) - 1 = 3 种。

按照上面这种策略，

继续找第二个点，即点2，其不相邻的只有点3，因此一共有(2^2) - 1 = 3 种染色方案

继续找第三个点，即点3，其不相邻的只有点2，因此一共有(2^2) - 1 = 3 种染色方案

继续找第四个点，即点4，其不相邻的只有点1，因此一共有(2^2) - 1 = 3 种染色方案

此时，我们发现除了全黑的染色方案外，一共有3*4 = 12种染色方案，但是实际上只有6种

整整多了一倍。

原因很简单，我们在统计第一个点的染色方案时，其实把第四个点的也统计了。统计第二个点时，把第三个点的染色方案也统计了。

因此后面对于第三个点和第四个点染色方案统计是重复的。 

因此，可得连通图的染色方案数目统计代码如下：

入参arr，即图中所有边 [v1, v2]，

入参m，即图中点的数量

// 连通图的染色方案
function getDyeCount(arr, m) {
  const graph = {};

  for (let [v1, v2] of arr) {
    graph[v1] ? graph[v1].push(v2) : (graph[v1] = [v2]);
    graph[v2] ? graph[v2].push(v1) : (graph[v2] = [v1]);
  }

  let count = 0;
  for (let v in graph) {
    const n = m - graph[v].length;
    count += (1 << n) - 1; // (2 ^ n) - 1
  }

  return (count >>> 1) + 1; // +1 对应全黑染色方案，count >>> 1 即 count / 2
}

本题，到此还未结束，因为题目中有一句话：

不能保证所有节点都是连通的

这说明什么呢？即，可能会出现下面这种情况：

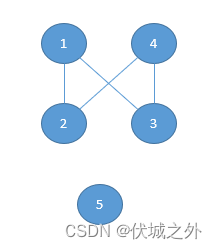
那么此时染色方案该如何统计呢？

题目和用例都没有说明清楚。。。。

我理解，应该统计每个连通分量的染色方案个数，然后求和作为题解。

即先统计1,2,3,4连通分量的染色方案个数为7，再统计5连通分量的染色方案为2，即一共有9个染色方案。

因此，本题还考察了连通分量的求解。

连通分量的求解可以使用并查集，关于并查集知识请看：华为机试 - 发广播_伏城之外的博客-CSDN博客 

算法源码

/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");

const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

const lines = [];
let m, n;
rl.on("line", (line) => {
  lines.push(line);

  if (lines.length === 1) {
    [m, n] = lines[0].split(" ").map(Number);
  }

  if (n !== undefined && lines.length === n + 1) {
    const arr = lines.slice(1).map((line) => line.split(" ").map(Number));

    console.log(getResult(arr, m));

    lines.length = 0;
  }
});

/**
 *
 * @param {*} arr 边，即[v1, v2]
 * @param {*} m 点数量
 */
function getResult(arr, m) {
  const ufs = new UnionFindSet(m);

  for (let [v1, v2] of arr) {
    ufs.union(v1, v2);
  }

  const cates = {}; // cates对象每个属性对应一个连通分量
  for (let i = 1; i < ufs.fa.length; i++) {
    let fa = (ufs.fa[i] = ufs.find(i));
    cates[fa] ? cates[fa].push(i) : (cates[fa] = [i]);
  }

  let count = 0;
  for (let k in cates) {
    // 连通分量中点的个数
    const len = cates[k].length;
    const set = new Set(cates[k]);
    // 如果输入1~n+1行的边中还有连通分量中的点，则将边计入同一个连通图connect中
    const connected = arr.filter(([v1, v2]) => set.has(v1) || set.has(v2));
    // 求连通图的染色方案个数
    count += getDyeCount(connected, len);
  }

  return count;
}

// 并查集
class UnionFindSet {
  constructor(n) {
    this.fa = new Array(n + 1).fill(0).map((_, i) => i);
  }

  find(x) {
    if (x !== this.fa[x]) {
      return (this.fa[x] = this.find(this.fa[x]));
    }
    return x;
  }

  union(x, y) {
    const x_fa = this.find(x);
    const y_fa = this.find(y);

    if (x_fa !== y_fa) {
      this.fa[y_fa] = x_fa;
    }
  }
}

// 连通图的染色方案
function getDyeCount(arr, m) {
  const graph = {};

  for (let [v1, v2] of arr) {
    graph[v1] ? graph[v1].push(v2) : (graph[v1] = [v2]);
    graph[v2] ? graph[v2].push(v1) : (graph[v2] = [v1]);
  }

  let count = 0;
  for (let v in graph) {
    const n = m - graph[v].length;
    count += (1 << n) - 1; // (2 ^ n) - 1
  }

  return (count >>> 1) + 1; // +1 对应全黑染色方案，count >>> 1 即 count / 2
}