大家好,我是北山啦,本文简单介绍Python数据结构的相关内容,简单就是很简单的那种
文章目录
- 查找
- 线性查找 O(n)
- 二分查找(Binary Search) O(logn)
- 排序
- 排序Low B三人组
- 冒泡排序
- 选择排序
- 插入排序
- 排序NB三人组
- 快速排序
- 归并排序
- 数据结构
- 栈和队列
- 栈
- 队列
- 应用
- 链表
- 贪心算法
- 例如:找零问题:钱数量最少
- 例子:背包问题:价值最多
- 例子:数字拼接问题:整数最大
- 活动选择问题:活动个数最多
- 动态规划
- 钢条切割问题
查找
线性查找 O(n)
def linear_search(li,val):
for ind,v in enumerate(li):
if v == val:
return ind
else:
return None
二分查找(Binary Search) O(logn)
二分查找:又叫这半查找,从有序列表的初始候选去li[0:n]开始,通过对待查找的值与候选去中间值的比较,可以使候选区减少一半
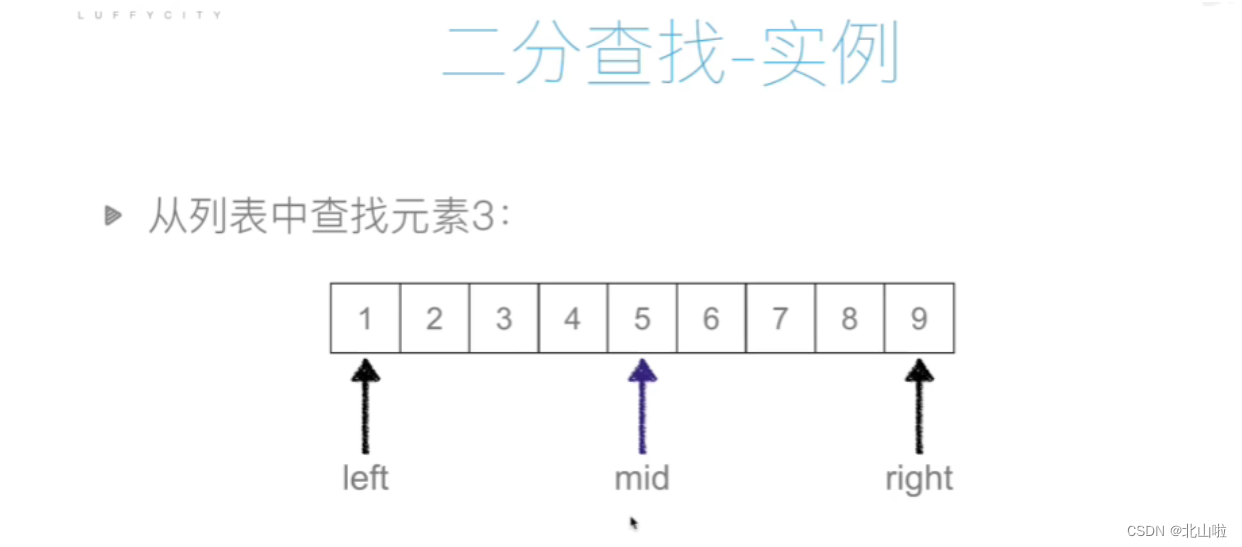
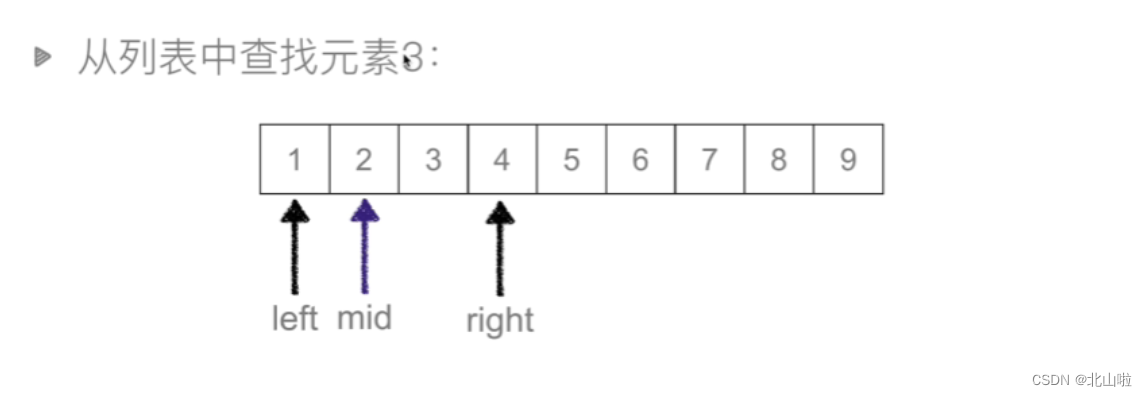
def binary_search(li,val):
left = 0
right = len(li) - 1
while left <= right: #候选区还有值
mid = (left + right) // 2
if li[mid] > val:
right = mid - 1
elif li[mid] < val:
left = mid +1
else:
return mid
else:
return None
#binary_search([1,23,2,5,4],1)
binary_search([1,23,2,5,4],1)
0
排序
- 排序就是将一组’无序’的记录顺序调整为有序的记录顺序,升序与降序,内置排序函数sort()

排序Low B三人组
- 冒泡排序
- 选择排序
- 插入排序
冒泡排序
列表每两个相邻的数,如果前面比后面的大,则交换这两个数
一趟排序完成之后,则无序区减少一个属,有序区增加一个数
关键词:躺、有序区、无序区范围
时间复杂度为O(n^2)
def bubble_sort(li):
for i in range(len(li) - 1):
for j in range(len(li) - i - 1):
if li[j] > li[j+1]:
li[j],li[j+1] = li[j+1],li[j]
import random
li = [random.randint(0,100) for i in range(100)]
print(li)
bubble_sort(li)
print(li)
[25, 55, 20, 14, 85, 57, 87, 21, 81, 15, 49, 97, 15, 64, 57, 6, 55, 12, 18, 79, 26, 84, 38, 45, 39, 74, 19, 2, 6, 60, 39, 27, 61, 53, 35, 73, 83, 84, 46, 62, 54, 83, 5, 76, 11, 13, 8, 73, 58, 79, 66, 96, 96, 39, 11, 56, 48, 84, 45, 94, 17, 41, 82, 34, 42, 45, 90, 70, 64, 32, 38, 7, 60, 76, 9, 38, 47, 75, 0, 48, 31, 47, 85, 23, 42, 57, 37, 29, 59, 56, 10, 25, 54, 90, 84, 32, 49, 61, 50, 63]
[0, 2, 5, 6, 6, 7, 8, 9, 10, 11, 11, 12, 13, 14, 15, 15, 17, 18, 19, 20, 21, 23, 25, 25, 26, 27, 29, 31, 32, 32, 34, 35, 37, 38, 38, 38, 39, 39, 39, 41, 42, 42, 45, 45, 45, 46, 47, 47, 48, 48, 49, 49, 50, 53, 54, 54, 55, 55, 56, 56, 57, 57, 57, 58, 59, 60, 60, 61, 61, 62, 63, 64, 64, 66, 70, 73, 73, 74, 75, 76, 76, 79, 79, 81, 82, 83, 83, 84, 84, 84, 84, 85, 85, 87, 90, 90, 94, 96, 96, 97]
冒泡排序改进
# l2 = [9,8,7,1,2,3,4,5,6]
# print(l2)
# bubble_sort(l2)
def bubble_sort(li):
for i in range(len(li) - 1):
exchange = False
for j in range(len(li) - i - 1):
if li[j] > li[j+1]:
li[j],li[j+1] = li[j+1],li[j]
exchange = True
if not exchange:
return
li = [1,2,3,4,5] #改进后只需要一趟,而改进前需要n-1趟
选择排序
每次选择最小or最大的加入新的列表当中
def select_sort_simple(li):
li_new = []
for i in range(len(li)):
min_val = min(li)
li_new.append(min_val)
li.remove(min_val)
return li_new
select_sort_simple([3,4,5,61,3,3])
[3, 3, 3, 4, 5, 61]
改进
def select_sort(li):
for i in range(len(li) - 1):#i是第几趟
min_loc = i
for j in range(i+1,len(li)):
if li[j] < li[min_loc]:
min_loc = j
li[i],li[min_loc] = li[min_loc],li[i]
return li
select_sort([3,4,5,61,3,3])
[3, 3, 3, 4, 5, 61]
插入排序
插入排序是一种简单直观的排序算法,其基本思想是将未排序的元素插入到已排序的序列中,从而得到一个新的排序序列。
插入排序的实现步骤如下:
将第一个元素看作已排序序列,从第二个元素开始遍历未排序序列;
每次遍历到一个新元素时,将它插入到已排序序列中的合适位置;
重复步骤2,直到遍历完所有未排序元素。
def insert_sort(li):
for i in range(1,len(li)):
j = i-1
temp = li[i]
while j >= 0 and li[j] > temp:
li[j+1] = li[j]
j -= 1
li[j+1] = temp
return li
排序NB三人组
- 快速排序
- 堆排序
- 归并排序
快速排序
快速排序是从冒泡排序演变而来的算法,但是比冒泡排序要高效得多,所以叫做快速排序。快速排序之所以快速,是因为它使用了 “分治法”。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WE7G9k05-1687183591926)(attachment:image.png)]](https://img-blog.csdnimg.cn/f0d07af8a562448db6470513cc617a9e.png)
具体思想:
def quick_sort(data,left,right):
if left < right:
mid = partiton(data,left,right)
quick_sort(data,left,mid-1)
quick_sort(data,mid+1,right)
代码实现:
def quick_sort(li):
if len(li) <= 1:return li
left,right = [],[]
mid = li[0]
for i in range(1,len(li)):
if mid > li[i]:
left.append(li[i])
else:
right.append(li[i])
return quick_sort(left) + [mid] + quick_sort(right)
print(quick_sort([1,23,1,2,14,3,2]))
[1, 1, 2, 2, 3, 14, 23]
归并排序
归并排序是创建在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用
分治法:
分割:递归地把当前序列平均分割成两半
集成:在保持元素顺序的同时将上一步得到的子序列集成到一起(归并)

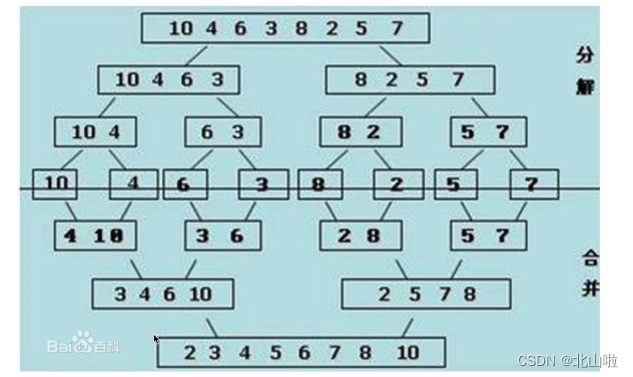
from heapq import merge
def merge_sort(li):
if len(li) <= 1:return li # 从递归中返回长度为1的序列
middle = len(li) // 2
left = merge_sort(li[:middle])
right = merge_sort(li[middle:])# 通过不断递归,将原始序列拆分成n个小序列
return list(merge(left,right))
merge_sort([11, 99, 33 , 69, 77, 88, 55, 11, 33, 36,39, 66, 44, 22])
[11, 11, 22, 33, 33, 36, 39, 44, 55, 66, 69, 77, 88, 99]
自己写的merge函数
def merge(left, right):
result = []
while len(left) > 0 and len(right) > 0:
# 左右两个数列第一个最小放前面
if left[0] <= right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
# 只有一个数列中还有值,直接添加
result += left
result += right
return result
merge_sort([11, 99, 33 , 69, 77, 88, 55, 11, 33, 36,39, 66, 44, 22])
[11, 11, 22, 33, 33, 36, 39, 44, 55, 66, 69, 77, 88, 99]
数据结构
数据结构是指相互之间存在着一种或者多种关系的数据元素的集合和该集合中数据元素之间的关系组成,简单来说,数据结构就是设计数据以何种方式组织并存储在计算机中
比如:列表、集合与字典等都是一种数据结构

栈和队列
栈

在Python中,一般使用列表结构即可实现栈
进栈:li.append()
出栈:li.pop()
取栈顶:li[-1]
队列


Python队列内置模块,使用方法:from collections import deque
-
创建队列:queue = deque()
-
进队:append()
-
出队:popleft()
-
双向队列队首进队:appendleft()
-
双向队列队尾出队:pop()
应用
栈的应用:括号匹配问题
括号匹配:给一个字符串,其中包括小括号、中括号、大括号,求该字符串中的括号是否匹配
参考代码:
https://blog.csdn.net/qq3342560494/article/details/128521756
https://cloud.tencent.com/developer/article/2040208
#定义要检查匹配的符号类型
brackets = {'}': '{', ']': '[', ')': '(', '>': '<'}
#将符号的正反向进行分类
bracket_l, brackets_r = brackets.values(), brackets.keys()
#定义一个检查字符串的方法
def check(str1):
alist = [] #定义一个空列表
for c in str1:
if c in bracket_l:
alist.append(c)#将左符号压入栈内
elif c in brackets_r:#右符号要么出栈,要么匹配失败,不做处理
if alist and alist[-1] == brackets[c]:#判断alist不会空且alist最后一个字符等于左符号对应的右符号时
alist.pop() #就做出栈操作
else:
return False
return True #传入空的字符串直接返回true
if __name__ == '__main__':
print(check("6c[*]{7b +[(8e -s3) * (d4+t5)]}<<>>"))
print(check("6c*{7b+ [8e- 9f]}<>"))
print(check(""))
True
True
True
栈和队列的应用–迷宫问题

栈–深度优先搜索-回溯法
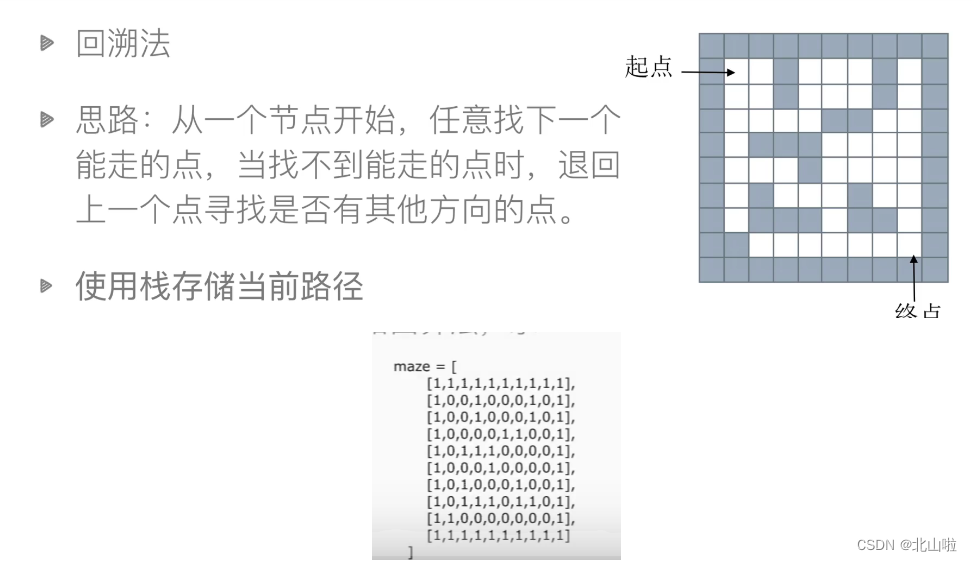
maze = [
[1,1,1,1,1],
[1,0,1,0,1],
[1,0,0,1,1],
[1,1,0,0,1],
[1,0,1,0,1]
]
#表示四个方向
dirs = [
lambda x,y:(x+1,y),
lambda x,y:(x-1,y),
lambda x,y:(x,y+1),
lambda x,y:(x,y-1)
]
def maze_path(x1,y1,x2,y2):
stack = []
stack.append((x1,y1))
while len(stack) > 0:
curNode = stack[-1] #出发位置
"""找到了终点,打印路线"""
if curNode[0] == x2 and curNode[1] == y2:
for p in stack:
print(p)
return True
for dir in dirs:
nextNode = dir(curNode[0],curNode[1])#走四个方向:x-1,y;x+1,y;x,y-1;x,y+1
#如果下一个节点能走
if maze[nextNode[0]][nextNode[1]] == 0:#0表示能走
stack.append(nextNode)#存入栈中
maze[nextNode[0]][nextNode[1]] = 2 #标记走过了的路
break
else:
maze[nextNode[0]][nextNode[1]] = 2
stack.pop()
else:
print('没有路')
return False
maze_path(1,1,3,3)
(1, 1)
(2, 1)
(2, 2)
(3, 2)
(3, 3)
True
链表
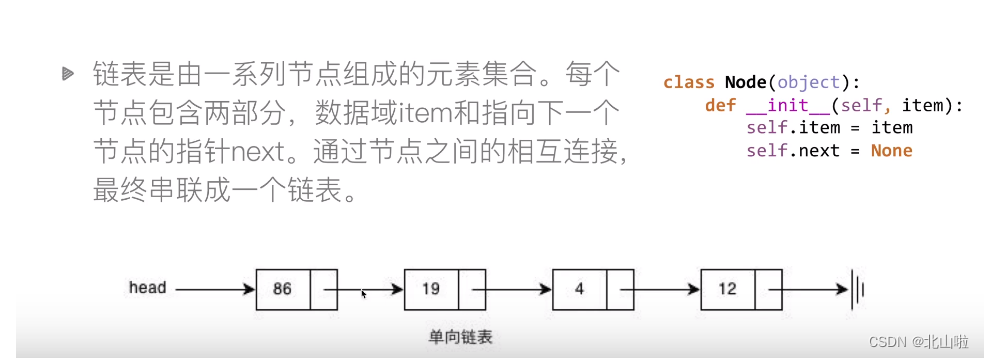
class Node:
def __init__(self,item):
self.item = item
self.next = None
a = Node(1)
b = Node(2)
c = Node(3)
a.next = b
b.next = c
print(a.next.next.item)
当然,链表的相关问题还很多,大家自行学习吧
贪心算法

例如:找零问题:钱数量最少
假设商家老板需要找零n元钱,钱币的面额又有:100元、50元、20元、5元、1元,如何找零使得所需钱币的数量最少?
t = [100,50,20,5,1]
def change(t,n):
m = [0 for _ in range(len(t))]
for i,money in enumerate(t):
m[i] = n // money
n = n % money
return m,n #m:对应t中的个数,n:表示剩余
change(t,35)
([0, 0, 1, 3, 0], 0)
例子:背包问题:价值最多
一个小偷在某个商店发现有n个商品,第i个商品价值vi元,重wi千克。他希望拿走的价值尽量高,但他的背包最多只能容纳w千克的东西,他应该拿走那些商品
- 0-1背包:对于一个商品,小偷要么把它完整拿走,要么留下,不能之拿走一部分,或把一个商品拿走多次。(金条)
- 分数背包:对于一个商品,小偷可以拿走其中任意一部分。(金沙)

对于分数背包问题,贪心算法是最优的
对于0-1背包问题,就不是了
goods = [(60,10),(100,20),(120,30)]#每个商品元组表示:(价格,重量)
goods.sort(key = lambda x:x[0]/x[1],reverse=True)
goods = [(60,10),(100,20),(120,30)]
goods.sort(key=lambda x:x[0]/x[1],reverse=True)
def fractional_backpack(goods,w):
m = [0 for _ in range(len(goods))]
total_value = 0
for i,(prize,weight) in enumerate(goods):
if w >= weight:
m[i] = 1
w -= weight
total_value += m[i]*prize
else:
m[i] = w / weight
total_value += m[i]*prize
w = 0
break
return total_value,m
print(fractional_backpack(goods,50))
(240.0, [1, 1, 0.6666666666666666])
对于0-1背包问题,贪心做不了,要用到动态规划
例子:数字拼接问题:整数最大
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-c0eRSwSn-1687183591968)(attachment:image.png)]](https://img-blog.csdnimg.cn/01a597710605424f9b69ddfb8d14b168.png)
a + b if a+b> b+a else b+a
from functools import cmp_to_key
li = [32,94,128,6,71]
def xy_cmp(x,y):
if x+y < y+x:
return 1
elif x +y > y +x:
return -1
else:
return 0
def number_join(li):
li = list(map(str,li))
li.sort(key = cmp_to_key(xy_cmp))
return ''.join(li)
print(number_join(li))
9471632128
def largest_number(nums):
nums = [str(num) for num in nums]
nums.sort(key=lambda x: x*10, reverse=True)
return ''.join(nums)
活动选择问题:活动个数最多
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3jLGL2nx-1687183591970)(attachment:image.png)]](https://img-blog.csdnimg.cn/5c1048a9bc8b4786b7ce8f5354b2c7e0.png)
利用反证法来证明:最先结束的活动一定是最优解的一部分
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-erUcBwBR-1687183591971)(attachment:image-2.png)]](https://img-blog.csdnimg.cn/9332056ba8e34d9cbb529469008e605c.png)
activities = [(1,4),(3,5),(0,6),(5,7),(3,9),(5,9),(6,10),(8,11),(8,12),(2,14),(12,16)]
activities.sort(key=lambda x:x[1])
def activities_selection(a):
res = [a[0]]
for i in range(1,len(a)):
if a[i][0] >= res[-1][1]:
res.append(a[i])
return res
print(activities_selection(activities))
[(1, 4), (5, 7), (8, 11), (12, 16)]
动态规划
利用递归来解决斐波拉契问题
def fibnacci(n):
if n== 1 or n==2:
return 1
return fibnacci(n-1) + fibnacci(n-2)
动态规划(DP)的思想 = 递推式 + 重复子问题
#动态规划的思想
def fibnacci_no_recurision(n):
f = [0,1,1]
if n >2:
for i in range(n-2):
num = f[-1] + f[-2]
f.append(num)
return f[n]
print(fibnacci_no_recurision(40))
102334155
钢条切割问题
某公司出售钢条,出售价格与钢条长度之间的关系如下:

问题:现有一段长度为n的钢条和上面的价格表,求切割钢条方案,使得总利益最大




#p = [0,1,5,8,9,10,17,17,20,21,23,24,26,27,27,28,30,33,36,39,40]
p = [0,1,5,8,9,10,17,17,20,24,30]
递归的方法来解决
def cut_rod_recurision_1(p,n):
if n == 0:
return 0
else:
res = p[n]
for i in range(1,n):
res = max(res,cut_rod_recurision(p,i) + cut_rod_recurision(p,n-i))
return res
cut_rod_recurision_1(p,9)
25
def cut_rod_recurision_2(p,n):
if n == 0:
return 0
else:
res = 0
for i in range(1,n+1):
res = max(res,p[i] + cut_rod_recurision_2(p,n-i))
return res
cut_rod_recurision_2(p,9)
25
![[Day 3 of 17]Building a document scanner in OpenCV](https://img-blog.csdnimg.cn/ebf4ca234a8948de9503262c55651dae.png)