FOC控制之小A小B小C是如何追求小D的

1、写在前面

随着电动汽车的热火，关于FOC控制技术的文章这几年在网络上可谓是一搜一大把，各种理论分析，公式推导，应有尽有。通过这些文章，可以看出大佬还是很多的。另外也有FOC的开源硬件。而在大几年前，第一次做这种项目的时候，想找个开源硬件参考下代码，搜遍了全球最大的同性交友网站（github），也没有找到。只找到一些开环的VF控制的。

而大几年前关于FOC控制技术，是各个芯片公司的独家秘笈。一般是不外传的，只对合作方开放。比如TI的电机控制库，ST的motor control workbench3.0 4.0啥的，英飞凌也有，现在想不起来是什么了，特别是ST的库，以及ST举办的开发者技术交流论坛，流传的一个PPT，是众多电机开发者入门的宝典，包括我个人。在此也要感谢ST，现在用的国产芯片，他们电机库我看了一遍，有一种直觉，这就是ST的复刻版啊。

再写一篇理论性的文章，我个人觉得完全没有必要，一方面是网络上确实是太多了，多我一篇不多，少我一篇不少。另一方面，写这种文章比较耗费精力，画图，列公式，推导，写这种理论文章的意义就是自己再复习一遍。所以这里就不写了。就把一些优质资源列出来供大家参考，意义更大一些。

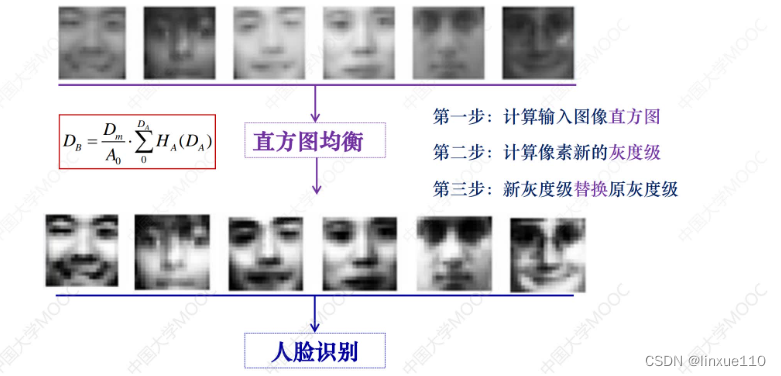
ABC是电机的三相，Q是力矩，D是磁链。

2、FOC的一些概念

2.1、BLDC和PMSM

关于电机，很多人开始的时候容易搞混BLDC和PMSM的概念，本质上这两种电机其实从结构形式上是一样的。唯一的区别是转子上的磁钢，一个是方波一个是正弦波。再准确点的讲，BLDC一般是用多块磁钢贴在转子上，这就导致了磁场是不连续的，形成了方波磁场。而PMSM的转子磁钢是一个整体圆环，充磁的时候径向正弦波充磁，充出我们需要的极对数。下图这种就是典型的BLDC。
在这里插入图片描述

大家看了很多文章，知道PMSM的转矩波动小，BLDC的转矩波动大。而决定这个转矩波动的就是充磁方式和磁钢安装方式决定的。通过几种方式我们可以轻易的分别这两种电机。一个是用手去转转子，感受齿槽效应，很小，甚至感受不到的一般都是PMSM，最稳妥的办法就是直接拿示波器测量旋转反电动势。反电动势波形是正弦波的就是PMSM，方波的就是BLDC。

FOC是一种矢量控制算法，这两种电机都可以控制，从我的实践看来，BLDC转起来会有轻微顿感，而PMSM是非常顺滑的。

2.2、控制流程

2.2.1 、从有刷电机到六步换向到FOC

我们知道一个直流有刷电机，给他通一个电他就开始转起来了，电压越高转的越快。小时候拆过玩具里面马达的都可以看到，这种电机后面是有一个碳刷换向器的，当然了，我们拆的那种就是两个铁片，没有碳刷。其实我们这种控制方式就是电流控制。如果用PWM调制一个电压来控制有刷直流电机，就可以轻松的改变电机旋转速度。

而三根线的这种无刷电机，直接这样通电，电机是不会转的，你给其中两根线通电，电机会卡死在某一个位置。你如果不断电的话，电机就会发热，最后可能烧毁。这个时候你再换两根线通电，电机会卡在另外一个位子，你再换两根线，电机又换一个位子，你如果速度足够快的去换着通电，电机就会按照你这个足够快的速度转起来，这就是6步换向控制。这是几年前大多数BLDC的控制方式。而实际控制过程中换向点需要比较准确，所以还要检测反向电动势过了中点。如果这个电机是一对级的，换一次相，那么电机走60度，六步换向刚好360度。那么在这个60度之间，我如果想让电机走15度或者走5度怎么办呢。通过六步换向这种方式明显是做不到了，这个时候我们就要用FOC控制了。FOC的中文翻译就是磁场向量控制。我们用一个很浅显的方式来理解他。如下图所示，如果A使出全部的力量，那么转子就转到A的位置，B使出全部力量，那么转子就靠在B的位子，如果A使出一半的力，B使出一半的力，那么转子就停在A和B的中间。这就好比，小A和小B一起追求小D，假设小D的人品有问题，小A发力的时候，小D就靠近小A，小B发力的时候，小D就靠近小B，而小A和小B一起发力，且势均力敌，小D就游走中间。这样的话，控制好小A和小B的发力尺度，通过三角函数，我们就能算出小D游走在哪个位子。如果小D走到了小B和小C的区间，那么小D就会受到小B和小C的拉扯了。这就是FOC控制的精髓。这样的话，我们就可以控制转子运动到任何一个地方了。
在这里插入图片描述

2.2.2、如何做到FOC

如何轻松控制小A和小B的发力程度呢，电机三根线，究竟该如何控制呢。上世纪七十年代，西门子公司的工程师Blaschke发表了一篇论文，如下所示：

在这里插入图片描述

巧妙的把三根电机线的控制等效成类似于有刷电机的两根线控制。那么具体是如何等效的，其实初中的知识就可以做到了。就是一个clark变换。如下图所示，Ia，Ib，Ic转换到α和β的直角坐标系。
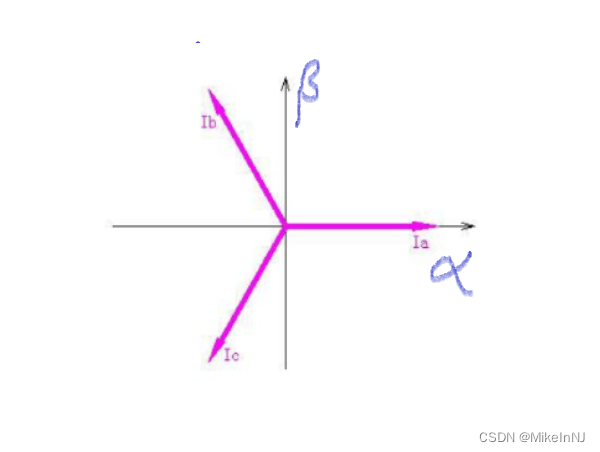
在这里插入图片描述

Iα 等于Ia减去Ib和Ic在α轴上的分量，Ib乘以cosθ就是Ib在阿尔法轴上的投影。所以：
$I α = I a - c o s θ * I b - c o s θ * I c$
而θ很明显是60度。同理可以得到：
$I β = s i n θ * I b - s i n θ * I c$

写成矩阵形式就是：

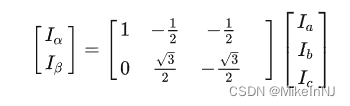
在这里插入图片描述

为什么要写成矩阵形式？是不是有病，装高深，其实并不是，因为转成两个控制量，是方便了我们进行控制，但是最后还是要去控制实实在在的三根线啊，所以最后还要再转回去。一个向量乘以一个矩阵变成另一个向量，那么再变回去，我们就用另一个向量乘以这个向量的逆矩阵（线性代数）。这样就不用我们再傻不拉几的反着推导了。现在这个αβ坐标系是个静止的，我们要让他转起来，所以我们要把他变成旋转的坐标DQ坐标。如下图（借用了稚晖君的图，参考文献会给出稚晖君的链接）所示，如何旋转呢，三角函数大法继续，这个转换就是park变换。

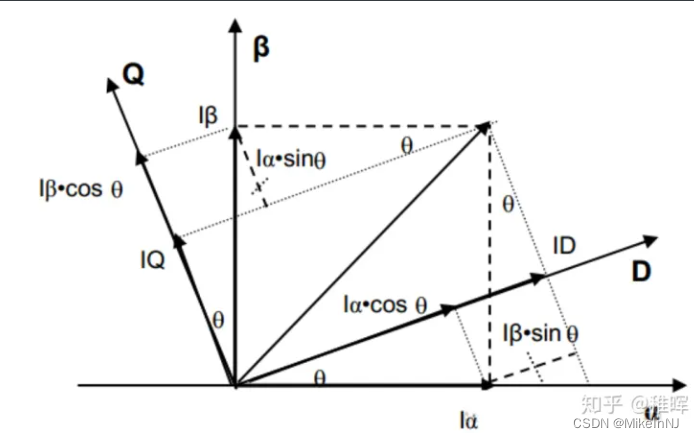
在这里插入图片描述

公式如下：

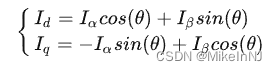
在这里插入图片描述

这个θ角度，可以通过编码器得到，或者反电动势估算，所以，这个θ角其实是已知的。这个时候，我们发现只要我们给Id和Iq一个值，然后给一个θ角度，然后反park变换，是不是我们就可以得到Ia，Ib，Ic三个控制量的值了。这就是FOC控制的核心思想和核心公式。

2.2.3、到底如何控制那三根线

看看FOC的经典控制过程图：

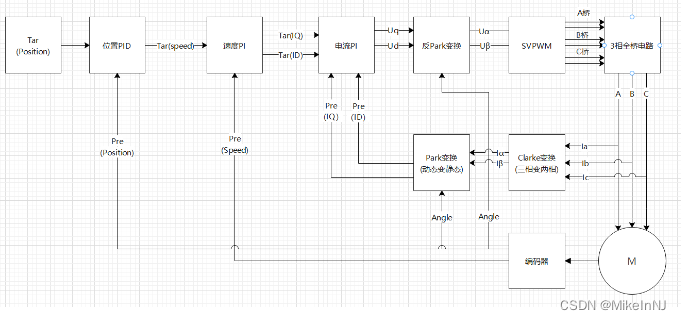
在这里插入图片描述

我们可以看到后面有一个SVPWM，这是个什么东西，其实这个SVPWM，是一个反clark变换器，同时也是一个pwm的调制器，先了解下pwm调制，占空比大，电压就大，占空比小电压就小。如下图所示，通过调节PWM的占空比，我们是不是就可以得到一个正弦波。你用示波器去测量电机的三个线，你会发现，里面其实就是这种波形。当然了，没有负半轴，这里的负半轴是为了方便理解。
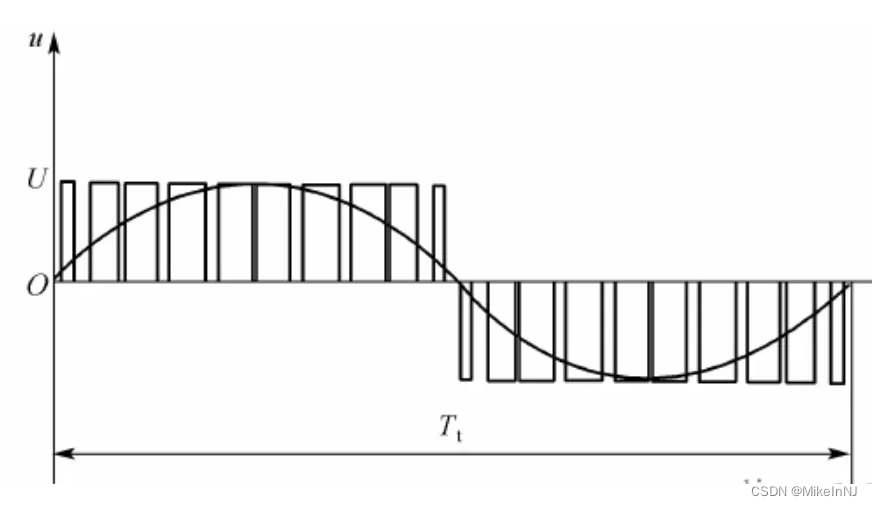
在这里插入图片描述

为了方便理解，我们取某一个时刻来看，这个时刻ABC三根线的电压是不变的，也就是小A和小B还有小C，他们之间的发力关系是不变的，这个时候小Q在那个θ角的位置。我们现在要让小Q在360°均匀游走，雨露均沾，我们就给Iq一个值，并且把对应的θ角实时的反馈到变换公式里，这样，小Q就会转起来。我们给的这个Iq值越大，小Q就转的越快。

SVPWM一句话来概括，就是根据Uα，Uβ（电流到电压是线性的）产生脉宽调制波形送给电机，而小A和小B具体发力的多少，其实是用时间来划分的，在单位时间内，小A作用时间长，那么小A做的功就多，伏秒平衡原则。具体参考下面这篇文章。涉及到互补性PWM，全桥控制电路等。

https://zhuanlan.zhihu.com/p/414721065