CABAC编解码原理分析

文章目录

CABAC编解码原理分析
一、二进制算数编码
二、CABAC编码
三、CABAC编解码与普通的二元算术编码的区别
四、 CABAC编解码中各个变量的计算：
五、一些其他问题：
六、总结：
七、参考资料

一、二进制算数编码

cabac是一种特数的二进制算数编码，假设我们有由“0”和“1”组成的字符串需要编码，且“0”和“1”的出现的概率概率分别为0.4和0.6，那么我们分配如下初始概率区间：

0	1
[0, 0.4)	[0.4, 1]

我们按照这个概率区间对“1100”进行编码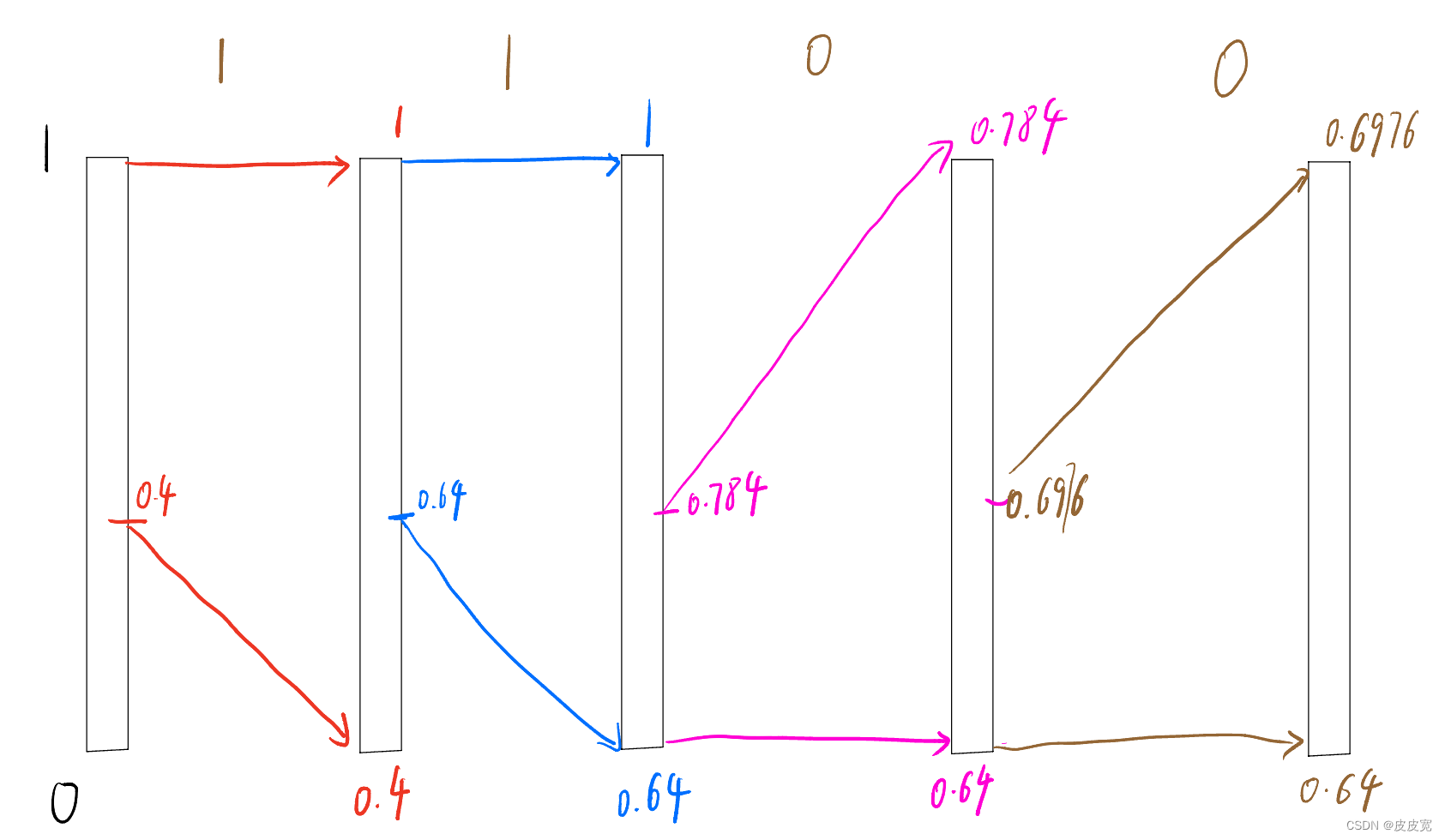请添加图片描述

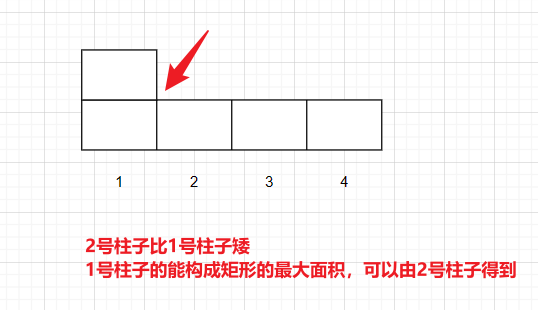
1，如图所示，编码第一个“1”时，区间长度为1，（0，0.4）为“0”的编码区间，（0.4，0.6）为“1”的编码区间，因此第一个“1”编码完成后，区间长度L变为0.6（0.4~1）；此时重新划分编码区间区间长度 $L = 1 - 0.4 = 0.6$ ; 因此“0”的编码区间变为(0.4，0.4+L*0.4),也就是（0.4，0.64）；
2，依次类推。将 1100这四个数编码完成后，编码区间为（0.64，0.6976），我们取这个区间的任意一个数，就能在知道长度和编码概率的情况下，恢复这个数；
3，假设我们取0.65，解码端恢复这个数时，首先判断0.65在（0.4，1）这个区间，因此第一位为“1”，再判断其在（0.64，1）这个区间，因此第2位也是“1”，依次类推，可恢复编码前的数据“1100”，当然了，这种编码方式需要知道原始数据的长度和编码后的区间，不然会一直判断下去；

二、CABAC编码

🐺我们以上的编码是按照，0出现的概率为0.4，1出现的概率为0.6来进行编码的，但实际应用中，我们怎么得到这个真实的概率呢？
🐰CABAC中我们根据如下几个条件对其进行分类，有一张大的查找表look_up确定每个分类的“0”和“1”的概率：

1，不同的语法元素
2，该宏块(MB)的上方宏块，左面宏块的情况；
3，该语法元素的比特位

举个例子，假设一个4bit的语法元素，syn;

🐸首先我们判断上方宏块的情况condA（上方宏块可访问则condA为1，否则为0）, 和左面宏块的编码情况condB(上方宏块可访问则condB为1，否则为0), syn语法元素的基准值为Ctxoffset(查表确定，这里假设为0)，偏差Ctxinc = f(condA, condB, bin), 这里的bin代表当前编码是第几个比特，f(condA, condB, bin)的表达式每个语法元素都不一样，需要翻书确认（详见参考资料【4】）本文假定Ctxinc = f(condA, condB, bin) = condA + condB + bin，总的查表地址如下所示
$Ct x i d x = Ct x o ff se t + Ct x in c = Ct x o ff se t + f (co n d A, co n d B, bin)$
🐯假设syn为1100，且上方和左方的宏块都不可获取（比如最左上角的宏块），

我们编码第一个“1”时，计算Ctxidx = 0，从 look_up[0]中获取此时1和0的概率，进行编码，由于编码的是“1”，因此我们编码完成后需要增大look_up[0]中“1”的概率，减小0的概率；
编码第二个“1”时，Ctxidx = 1, 我们同样先从 look_up[1]中获取此时1和0的概率，进行编码，由于编码的是“1”，因此我们编码完成后需要增大look_up[1]中“1”的概率，减小0的概率；
我们编码第三个“0”时，计算Ctxidx = 2，从 look_up[2]中获取此时1和0的概率，进行编码，由于编码的是“0”，因此我们编码完成后需要增大look_up[2]中“0”的概率，减小1的概率；
编码第四个“0”时，Ctxidx = 3, 我们同样先从 look_up[3]中获取此时1和0的概率，进行编码，由于编码的是“0 ”，因此我们编码完成后需要增大look_up[3]中“0”的概率，减小1的概率；

也就是说, CABAC会在编码过程中不断的更新该情况下“0”“1”出现的概率，以求编码时用到的概率趋近于真实的概率；
至于概率和编码的关系，就需要参考香农定理了，网上有很多，这里就不多做解释了；

三、CABAC编解码与普通的二元算术编码的区别

2.1 cabac里面1，和0出现的概率是不断变换的：
🐶cabac编码为每个语法元素的每个bit都分配了一个概率模型；每个语法元素的概率模型的基地址为Ctxoffset，根据上方和左边LCU的情况，计算出每个比特的偏移地址ctxinc，从而得到ctxIdk = ctxoffset + ctxinc;
🐭在一个slice开始时，为每个模型分配一个初始概率值，每编码1bit，对该bit的概率模型进行更新；
2.2 cabac输出编码区间的溢出情况：
🐹普通二元算术编码的编码区间越来越小，最终输出一个很小的区间；
🐰cabac则是设定区间大小为【0，510】，当区间小于256时，就扩大区间，并输出0/1的方式，记录扩大区间的情况（书中称为“归一化”）。
🐸解码时，初始区间为【0，510】，根据编码端扩大区间时输出的码流（书中记为OFFSET，也就是“区间归一化”过程输出的码流），来还原区间变化过程，从而达到解码的作用；
🐶这个归一化的过程有点复杂，可以简单理解为当编码区间变为（0.6，1）时，那么无论后面怎么编码，最终的编码出的值都肯定大于0.5，我们就现输出一个0.5，即小数位的第一个比特是1，当编码区间变为（0.6，0.75）时，无论后面怎么编码，肯定都小于0.75，因此小数位第二位肯定是0，此时就可以先输出个“0”，虽然不准确，但大概就是这么个意思；

四、 CABAC编解码中各个变量的计算：

🐨LPS ：低概率符号（0或1，如1.1所说，概率是会变化的）
🐻MPS ：高概率符号（1，或0，与LPS相反）
🐷L，Ｒ：区间左边界和区间长度；【0，510】就是L=0，R=510；
🐽 $R_{LPS}$ ： LPS编码区间的长度；
🐮 $R_{MPS}$ ：MPS编码区间的长度；
🐗编码区间【L ， L+R】 = 【L，L+R—LPS】【L+R—LPS， L+R】
🐵 $\sigma$ ：代表MPS的概率，这个值越大，MPS对应的概率越大
🐒 $o ff se t$ : 初始为编码出来的前9bit码流；
🐴readbits(1) : 表示读入1bit码流，用于解码时更新offset值，从而更新编码区间

🐎 🐫 🐑 🐘 🐼 🐍 🐦 🐤 🐥 🐣 🐔 🐧 🐢 🐛 🐝 🐜 🐞 🐌 🐙 🐠

五、一些其他问题：

5.1 怎么判断一个语法元素结束了呢？
🐎 这个和二值化的方式有关，比如FL二值化，有cmax；U则是0为一个语法元素的最后1bit;
5.2 怎么判断当前编码或解码的元素是什么？
🐫编码时，语法元素有严格的编码条件和编码顺序，比如h264的编码，若为p帧，第一个一定是编码mb_skip_flag，若mb_skip_flag为0，下一个必定编码mb_type，若mb_type为pcm，则必定编码残差系数;
🐑解码端同理，若为p帧，第一个一定解码mb_skip_flag，若解码出的mb_skip_flag为0，下一个语法元素一定是mb_type，否则是end_of_slice_flag，知道下一个编码的语法元素，自然就知道其对应的ctxoffset，二值化方式等信息了;