6 从0开始学PyTorch | 构建模型、损失函数、广播机制

前面都在学一些PyTorch的基本操作，从这一节开始，真正进入到模型训练的环节了。原作者很贴心的一步步教我们实现训练步骤，并且还从一个最简单的例子出发，讲了优化方案。

宏观上的训练过程

image.png

当然这里所说的训练还没有到深度学习那一步，如上图所示，有一批输入数据，这些数据是有噪声的。数据分成两份，一个是训练集，一个是验证集。在构建训练的时候，我们需要先预设一个模型，假定通过这个模型能够得到我们想要的结果。把训练集数据输入到模型里面（称为forward前向传播），然后观察模型输出的结果跟我们预先已知的结果（称为ground truth）进行对比，得到预测结果和实际结果的差距（称为loss），然后分析如何改变我们的模型权重（weight）来减小这个差距，这里会涉及到一个概念gradient（梯度），分析的方法是使用复合函数的导数链式法则，称为backward（反向传播）。这些概念不懂没关系，后面会讲，我也会仔细学习，有不对的地方也欢迎大家指正。

再说到下面的一小撮验证集，这些数据也用模型去进行运算，但是对它们的运算结果并不进行反向传播，从而不会影响模型的训练，只是用来检测模型在未知数据上的效果，这里就会有过拟合和欠拟合的概念。

一个例子

大概的流程介绍了，我们还是来实际搞一个项目吧。
项目背景：我去外面旅游买了一个温度计，上面有一些刻度值，但是这些值跟我平时用的摄氏温度明显不一样，我想搞一个模型来研究怎么把这个温度计的数字转换成我熟悉的摄氏温度，从而能够让我在看这个温度计的时候看得明白。

这时候我取出已经包浆的82年温度计，这个温度计是以摄氏温度进行计数的，因此我能够很容易明白，在同一时刻分别记录这两个温度计的数值，多记录几轮就构建起了我们的数据集。

在Jupyter上先设定好引用及配置

%matplotlib inline
import numpy as np
import torch
torch.set_printoptions(edgeitems=2, linewidth=75)

看下我们收集的数据，t_c表示Celsius temperature摄氏温度，t_u表示Unknown temperature 未知温度，总共11组。然后把这数据转换成tensor。

t_c = [0.5,  14.0, 15.0, 28.0, 11.0,  8.0,  3.0, -4.0,  6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c)
t_u = torch.tensor(t_u)

这里我们把这个温度的散点图画出来

import matplotlib.pyplot as plt

 # 创建画布
fig = plt.figure()
plt.scatter(t_u, t_c, c='b', edgecolors='r')
plt.show()

用未知温度作为x轴，摄氏温度作为y轴。按说如果两个温度计都是非常精确的，那么所有的点应该都落在一条直线上，不过那样的话就没办法解释我们后面要做的一堆操作了，所以这里算是给数据增加了一些噪声，可以看到这些点有一个整体的趋势，但也不是特别的精确，在实际解决的问题中一般都是不精确的，不然还用啥深度学习模型，直接写一个公式就解决了。

image.png

根据图上的结果，这里我们假设一个情况，就是t_u和t_c符合线性相关，就像下面这种公式
t_c = w * t_u + b，这里的w就是权重，b是偏置（bias），这是一种理想情况，就是有确定的w和b使得所有的t_u经过运算之后恰好等于t_c。接下来要做的就是想办法估算出w和b的具体值，实际情况是通过w和b运算，使得输出的结果尽可能接近t_c，因为我们前面也看到了数据并不是一条直线。

损失函数

损失函数也可以叫代价函数，前面简单提到了，损失函数就是计算预测结果和实际结果差距的函数，机器学习的过程就是试图将损失函数的值降到最小。

上面我说t_c = w * t_u + b这个公式是一个理想状况，实际上输出是一个预测结果，我们认为是t_p=w*t_u + b。loss函数就是要衡量t_p和t_c之间的差距。最简单的，我们可以取他们的差，比如|t_p - t_c|，这个计算方法是很常见的损失计算方法，也可以称为l1 loss，即平均绝对误差MAE，关于loss的事情就先不说太多了，后面可以考虑单独搞一个章节来讲loss，这里就知道这样去计算就ok了。除了直接相减，还可以用均方误差(t_p-t_c)的平方。

这两个loss function的图像如下，在差值为0的时候，这俩函数都有一个最小值，当t_c和t_p差距越来越大时，这两个函数都是单调递增的，且从0开始，斜率也是逐渐增加，当然对于左边这个，除了0点，其他位置的斜率是一样的。所以这俩都是凸函数。对于这种函数很容易找到最小值，但是如果我们处理的是自然语言这种东西，损失都不会是凸函数，所以在处理的时候也复杂的多。那些让人头大的问题先往后放放，这里我们先看今天的问题怎么解决。

image.png

先用代码实现我们的模型，有三个输入，即未知类型温度值，权重w和偏置b，输出1个结果就是我们前面说的t_p

def model(t_u, w, b):
    return w * t_u + b

然后编写损失函数，这里虽然定义的输入参数看起来是两个值，以及上面的model的输入看起来也都是单个数值，但实际上我们可以直接把tensor传进去进行运算，这就涉及到一个PyTorch的广播机制（深度学习里也会经常用到）。

def loss_fn(t_p, t_c):
    squared_diffs = (t_p - t_c)**2
    return squared_diffs.mean()

设定好了模型函数和损失函数，下面我们给一组初始化的参数，来运算一下，看看效果怎么样。从下面的代码可以看到，我们给出了w初始化为1，b初始化为0，然后进行运算，计算出了所有的t_p，然后计算均方误差高达1763，这显然不是我们想要的。

w = torch.ones(())
b = torch.zeros(())

t_p = model(t_u, w, b)
t_p

outs:tensor([35.7000, 55.9000, 58.2000, 81.9000, 56.3000, 48.9000, 33.9000,
        21.8000, 48.4000, 60.4000, 68.4000])

loss = loss_fn(t_p, t_c)
loss
outs:tensor(1763.8846)

我们肯定是期望这个loss越小越好，现在这么大的差距肯定是没办法接受的，我们可能想着去手动试探的修改参数，看看效果是否比之前好了，比如我们把w也设为0，这个时候给出的温度预测值也都是0，但是这个时候均方误差也要比之前强一些，甚至降到了之前的10分之一，只有187，真是让人激动啊。是不是觉得只要我们够勤奋，就能够找出最佳的参数。

w = torch.zeros(())
b = torch.zeros(())

t_p = model(t_u, w, b)
t_p
outs:tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])
loss = loss_fn(t_p, t_c)
loss
outs:tensor(187.3864)

不过实际的训练过程肯定不能这么傻，让你手动去修改参数值，像现在流行的预训练模型动辄有上亿的参数，你手动能改几个。不过关于自动化的进行运算和模型优化我们先留到下次介绍，这里先来理解一下广播机制。

广播机制（broadcasting）

我们先看看官方文档

In short, if a PyTorch operation supports broadcast, then its Tensor arguments can be automatically expanded to be of equal sizes (without making copies of the data).
翻译过来就是，如果一个PyTorch操作支持广播机制，输入这个操作的tensor参数会自动的扩展成相同的尺寸，并且没有实际复制数据。

这里先回顾一下大一的线性代数的知识：
对于两个尺寸不相同的矩阵是不能够进行加减运算的；
矩阵的相乘，它只有当左边矩阵的列数和右边矩阵的行数相同时才有意义比如AB(矩阵A乘以矩阵B)，而矩阵的除，我们一般是通过对右边的矩阵B求逆，最后和左边的矩阵A相乘得出结果

通过上面的两条小知识，可以看出，如果size不一样的tensor是很难进行运算的，而这里的广播机制就是制定了一些规则，使得在某些情况下，你不需要去手动构建符合运算的两个tensor，PyTorch会根据它自己识别到的情况进行自动的补全，并完成运算，而不去实际复制数据则节约了很多空间。

image.png

如果是正常的矩阵相加，需要向上面这个图所示的情况，而有了广播机制，下面图的情况也可以进行矩阵加法运算。

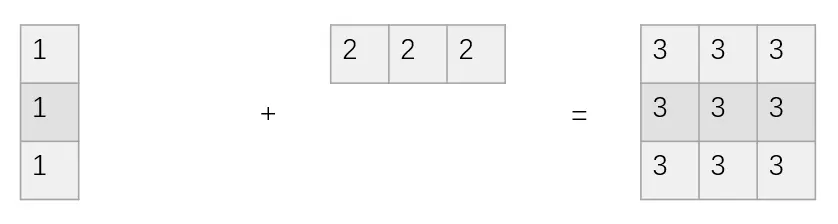
image.png

广播语法规则详情

规则原文

(1) Each tensor has at least one dimension.
(2) When iterating over the dimension sizes, starting at the trailing dimension, the dimension sizes must either be equal, one of them is 1, or one of them does not exist.

这个规则有两条，

第一条规定要使用广播机制，每个tensor至少有1维。
第二条规则规定当进行维度扩充的时候，从最后一个维度开始看起，然后维度要符合三种情况
A.两个维度size相等，那么就进行正常的运算。
B.其中一个维度的size为1，那么PyTorch会用这个维度上的单个项与另一个张量在这个维度上的每一项进行运算。
C.其中一个维度不存在，也就是一个张量的维度比另一个张量的维度大，那么另一个张量上的所有项将和这些维度上的每一项进行运算。

看一下代码

x = torch.ones(()) #关于这个用法我还没搞清楚，看起来产生了一个标量
y = torch.ones(3,1) #2维
z = torch.ones(1,3) #2维
a = torch.ones(2, 1, 1) #3维
print(f"shapes: x: {x.shape}, y: {y.shape}")
print(f"        z: {z.shape}, a: {a.shape}")
print("x * y:", (x * y).shape) #向量和标量运算，每一个直接乘上标量值，我理解这个不涉及广播
print("y * z:", (y * z).shape) #这个符合规则情况B，从最后一个维度看起，其中一个维度size为1，那么用y这个维度的单项与z这个维度的每一项相乘，然后倒数第二个维度z的size为1，同理，这个结果就是一个3*3的tensor。
print("y * z * a:", (y * z * a).shape) #然后这个符合情况C，a的维度数量和y * z的维度数量不一样
outs:shapes: x: torch.Size([]), y: torch.Size([3, 1])
        z: torch.Size([1, 3]), a: torch.Size([2, 1, 1])
x * y: torch.Size([3, 1])
y * z: torch.Size([3, 3])
y * z * a: torch.Size([2, 3, 3])

再举一个不符合要求的例子，这里倒数第三个维度上，两个size都不为1，就没办法运算了，这里就给出了一个错误，说这个2和3是不匹配的。

x = torch.ones(5, 2, 4, 1) 
y = torch.ones(3, 1, 1) 
x + y
---------------------------------------------------------------------------
RuntimeError                              Traceback (most recent call last)
<ipython-input-20-fd770c371507> in <module>
      1 x = torch.ones(5, 2, 4, 1)
      2 y = torch.ones(3, 1, 1)
----> 3 x + y

RuntimeError: The size of tensor a (2) must match the size of tensor b (3) at non-singleton dimension 1

说了这么多广播机制，我觉得对广播机制的实现还不是那么的熟悉理解，不过应该会随着具体应用的时候逐渐了解它。

今天这节就先写这么多，我累了。