柱状图中最大的矩形

⛅前言

大家好，我是知识汲取者，欢迎来到我的LeetCode热题100刷题专栏！

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。在此专栏中，我们将会涵盖各种类型的算法题目，包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等，并会提供详细的解题思路以及Java代码实现。如果你也想刷题，不断提升自己，就请加入我们吧！QQ群号：827302436。我们共同监督打卡，一起学习，一起进步。

LeetCode热题100专栏🚀：LeetCode热题100

Gitee地址📁：知识汲取者 (aghp) - Gitee.com

题目来源📢：LeetCode 热题 100 - 学习计划 - 力扣（LeetCode）全球极客挚爱的技术成长平台

PS：作者水平有限，如有错误或描述不当的地方，恳请及时告诉作者，作者将不胜感激

🔒题目

原题链接：84. 柱状图中最大的矩形

🔑题解

解法一：暴力枚举（中心扩散算法）

暴力枚举的思路比较简单，每次枚举一个柱子，以这个柱子为中心，并且以当前这个柱子为最短板，向左右两边扩散，如果遇到小于当前柱子高度的柱子，则停止扩散，因为要确保中心的柱子是最短版，这样做就能保障每一个柱子都能得到一个最大矩形面积，而我们最终的结果就包含在这每一个柱子求出来的最大矩形面积，因此我们还需要使用一个变量来更新迭代得到最终的结果(●ˇ∀ˇ●)

我们现在对上面的话进行一个精简，总结起来就是如下几步：
- Step1：枚举每一个柱子
- Step2：中心扩散。选定我们枚举的柱子，以它为中心往左右扩散，保障中心的柱子是最短的
- Step3：计算并迭代最大矩形面积。每次枚举一个柱子都能得到以该柱子为中心的最大矩形的面积，同时比较当前的最大矩形面积，如果比当前最大矩形面积还大，就更新最大面积；如果更小，就保留原有的最大矩形面积
但是这题是困难题，一般暴力枚举是很难通过的，所以这里也就只是提供一个思路，锻炼一下逻辑思维

PS：关于中心扩散算法还可以看【打卡第5天：5.最长回文子串】

示例1数据的图解：
```
/**
 * @author ghp
 * @title
 */
class Solution {
    public int largestRectangleArea(int[] heights) {
        // 遍历每一个柱子
        int ans = 0;
        for (int i = 0; i < heights.length; i++) {
            // 往左遍历
            int l = i;
            while (l > 0 && heights[l - 1] >= heights[i]) {
                l--;
            }
            // 往右遍历
            int r = i;
            while (r < heights.length - 1 && heights[r + 1] >= heights[i]) {
                r++;
            }
            // 计算当前柱子能形成矩形的最大面积
            int width = r - l + 1;
            // 更新矩形的最大面积
            ans = Math.max(ans, width * heights[i]);
        }
        return ans;
    }
}
```
复杂度分析：
- 时间复杂度： $O(n^2)$
- 空间复杂度： $O (1)$
其中 $n$ 为数组中元素的个数
解法二：单调栈

这题考的基础模型其实就是：在一维数组中对每一个数找到第一个比自己小的元素。这类“在一维数组中找第一个满足某种条件的数”的场景就是典型的单调栈应用场景。——摘自LeetCode上一位大佬的评论

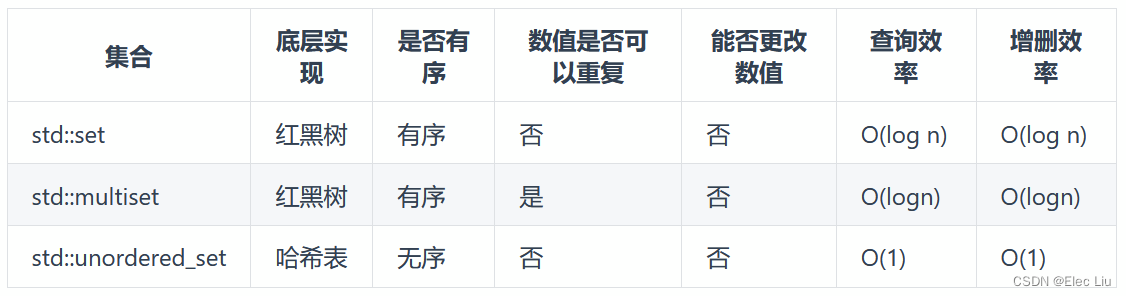
什么是单调栈？单调栈（Monotonic Stack）是一种特殊的栈数据结构，用于解决一类相关的问题，例如寻找下一个更大元素或者下一个更小元素等。单调栈的特点是栈中维持的元素满足某种单调性，可以是递增也可以是递减（本题是递增单调栈）。

单调栈的主要思路：使用一个栈，从左往右记录每一个柱子，当发现当前柱子比上一个柱子要矮，就计算上一个柱子能够得到的最大矩形的面积，为什么可以这样呢？因为当发现当前柱子比上一个柱子要矮时，说明上一个柱子的高度被限制了，上一个柱子能够组成的最大矩形的面积可以由当前这个较矮的柱子组成，这里画个图加以理解：

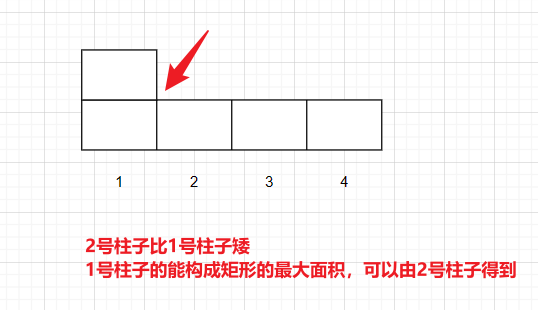
这样通过层层的迭代，就可以得到这一连串柱子能够组成矩形的最大面积了(●’◡’●)，而这个栈是一个递增的栈，栈中的柱子是递增的，发现矮的柱子就需要出栈，直到栈重新是递增的为止。

上面的话，总结起来就下面几步：
- Step1：从左往右枚举柱子。
- Step2：寻找比先入栈柱子的较矮柱子。发现较矮柱子，就可以计算最先入栈柱子的最大矩形面积，因为栈中的柱子的连续递增的，所以矩形的高是最先入栈的柱子，宽是当前柱子的索引减去最先入栈柱子的索引
- Step3：计算最大矩形面积，通过Step1和Step2可以计算出每一个柱子可以构成的最大矩形的面积，然后通过迭代更新，得出最终的结果
单调栈的思路很容易理解，但是实现起来感觉挺麻烦的，有很多需要注意的地方，比如：我们需要在栈的第一个元素和最后一个元素，添加一个0，用于最后的强制出栈，这一步是十分关键的，一般也很难想到，需要有一定的做题经验（大佬除外），所以说这一道困难题还是很有水准的 O(∩_∩)O
```
import java.util.ArrayDeque;
import java.util.Arrays;
import java.util.Deque;

/**
 * @author ghp
 * @title
 */
class Solution {
    public int largestRectangleArea(int[] heights) {
        int res = 0;
        Deque<Integer> stack = new ArrayDeque<>();
        int[] new_heights = new int[heights.length + 2];
        for (int i = 1; i < heights.length + 1; i++) new_heights[i] = heights[i - 1];
        System.out.println(Arrays.toString(new_heights));
        for (int i = 0; i < new_heights.length; i++) {
//            System.out.println("------------------------");
//            System.out.println("栈弹出前:"+stack.toString());
            while (!stack.isEmpty() && new_heights[stack.peek()] > new_heights[i]) {
                int cur = stack.pop();
//                System.out.println("栈弹出后:"+stack.toString());
//                System.out.println("面积为："+(i - stack.peek() - 1) * new_heights[cur]);
                res = Math.max(res, (i - stack.peek() - 1) * new_heights[cur]);
            }
            stack.push(i);
        }
        return res;
    }
}
```
复杂度分析：
- 时间复杂度： $O (n)$
- 空间复杂度： $O (n)$
其中 $n$ 为数组中元素的个数