【论文阅读】Adap-𝜏: Adaptively Modulating Embedding Magnitude for Recommendation

1. 来源

• 2023 WWW CCFA
• https://arxiv.org/pdf/2302.04775.pdf
• https://github.com/junkangwu/Adap_tau

2. 介绍

近年来，基于嵌入式嵌入的方法在推荐系统中取得了巨大的成功。

• 尽管它们的性能不错，但我们认为这些方法的一个潜在局限性——嵌入幅度没有被明确调制，这可能会加剧流行偏差和训练不稳定性，阻碍模型做出好的推荐。
• 它激励我们利用推荐中的嵌入规范化。通过将用户/项目嵌入规范化到一个特定的值，我们在四个真实世界的数据集上观察到令人印象深刻的性能提高（平均9%）。
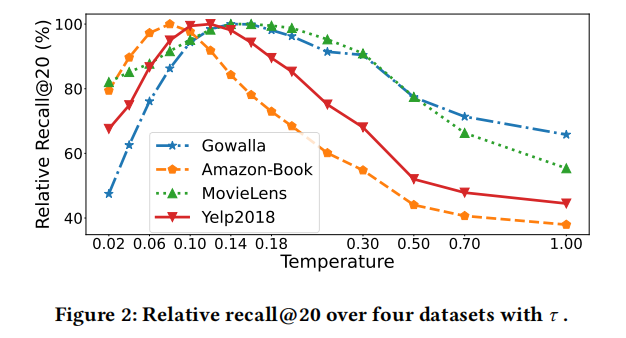
• 虽然令人鼓舞，但我们在推荐中应用归一化时也揭示了一个严重的限制——性能对控制归一化嵌入规模的温度 𝜏 的选择高度敏感。
• 为了充分培养归一化的优点，同时规避其局限性，本文研究了如何自适应地设置适当的 𝜏。为此，我们首先对𝜏进行了全面的分析，以充分了解其在推荐中的作用。然后，我们开发了一种自适应细粒度策略 Adap-𝜏，它满足四种理想的特性，包括自适应、个性化、效率和模型不可知。
• 作者进行了广泛的实验来验证该提案的有效性。该代码可以在 https://github.com/junkangwu/Adap_tau 上找到。

3. 模型解读

3.1 准备工作

在本节中，我们将介绍一些推荐系统的背景。

3.1.1 任务说明

假设我们有一个带有用户集 $U$ 和项目集 $I$ 的推荐系统。让 𝑛 和 𝑚 表示RS中的用户数量和项目的数量。收集到的隐式反馈可以用矩阵 𝑌∈{0,1}${}^{n\times m}$来表示，其元素 $y_{ui}$ 表示用户 $u$ 是否与一个项目 $i$ 进行了交互（例如，点击）。为方便起见，我们将整个交互的数据收集为 D={（𝑢，𝑖）|𝑦𝑢𝑖= 1}；将每个用户𝑢（项目𝑖）的交互项（用户）收集为P𝑢≡{𝑖|𝑦𝑢𝑖=1}（P𝑖≡{𝑢|𝑦𝑢𝑖= 1}）。RS的任务是为每个用户推荐他可能感兴趣的项目。

3.1.2 基于嵌入的模型

基于嵌入的方法在RS中得到了广泛的应用。他们首先将用户/项目特征（如id）转换为向量化表示（即e𝑢、e𝑖），然后根据嵌入的相似度进行预测。被广泛使用的相似度函数包括内积和神经网络。为了方便起见，本工作只采用具有代表性的内积进行分析，即模型预测可以表示为：

3.1.3 损失函数

训练推荐模型有多种损失函数选择，包括点态损失（如BCE、MSE）、成对损失（如BPR）和Softmax损失。最近的工作发现，Softmax损失可以减轻人气偏差，实现良好的训练稳定性，并与排名度量很好地一致。它通常比其他更好的性能，因此吸引了对推荐的兴趣。此外，Softmax损耗可以被认为是常用的BPR损耗的扩展。因此，我们将Softmax视为代表损失来作分析，可以表述为：

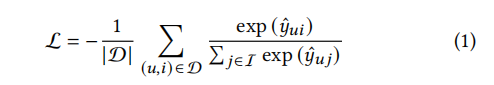
在实践中，经常包含一个日志操作，并进行负采样或小批处理策略来加速。但它们不是我们的重点，这里我们只是参考原始损失进行理论分析。

3.1.4 嵌入归一化

本工作研究了在推荐中嵌入规范化的性质。在内积的基础上，我们在预测中利用嵌入规范化如下：

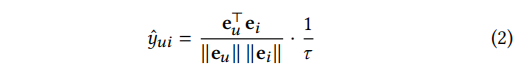
其中，用户/项目嵌入的大小已被重新调整。第一个因素：

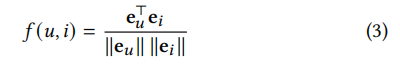
可以理解为余弦相似度，其中的大小已经被隔离；第二个因子 1/𝜏 重新调整了归一化嵌入。我们注意到，我们没有直接引入一个控制尺度的参数，而是在对比学习中借用了类似的想法，并利用了传统的温度。这种排列可以使我们的发现更好地推广到其他领域。

3.2 分析嵌入的规范化

在本节中，我们首先验证了在RS中利用嵌入规范化的本质。（3.2.1)，然后确定一个潜在的限制(3.2.2).最后，我们对温度进行了全面的分析，并揭示了它的两个重要作用 (3.2.3)。

3.2.1 规范化的必要性

• 理论分析。

  • 我们从理论分析开始，表明如果没有标准化，流行项目的大小比不受欢迎的项目增长得快得多。事实上，我们有：
    • 引理1。通过选择不控制大小的内积，我们在每次迭代中都有项目嵌入大小 𝛿𝑖 的变化：
      
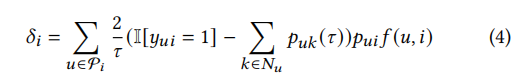
      在训练程序的早期阶段，𝛿𝑖 遵守：
      
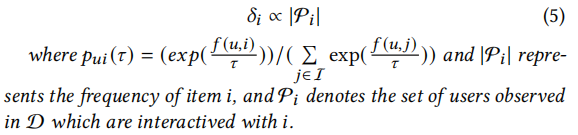
      该引理的证明方法见原文附录B.1。我们可以从Lamma 1中得出一个观察结果：请注意，在训练过程的早期阶段，用户和项目都是均匀分布的。换句话说，$p_{ui}f(u,i)$ 不能区分出显著的差异，${\sum }_{k\in N_u}{p}_{uk}(\tau )$相对较小，而流行项目的规模将获得 $|P_i|(I[y_{ui}=1])$ 的爆炸性上升。

• 实证分析。

  • 从引理1中，我们知道这个大小与项目的受欢迎程度相关。在本小节中，我们通过丰富的实验来探讨其对推荐的负面影响。
  • 实验设计。为了展示自由变化幅度的影响，这里我们进行了四个实验：
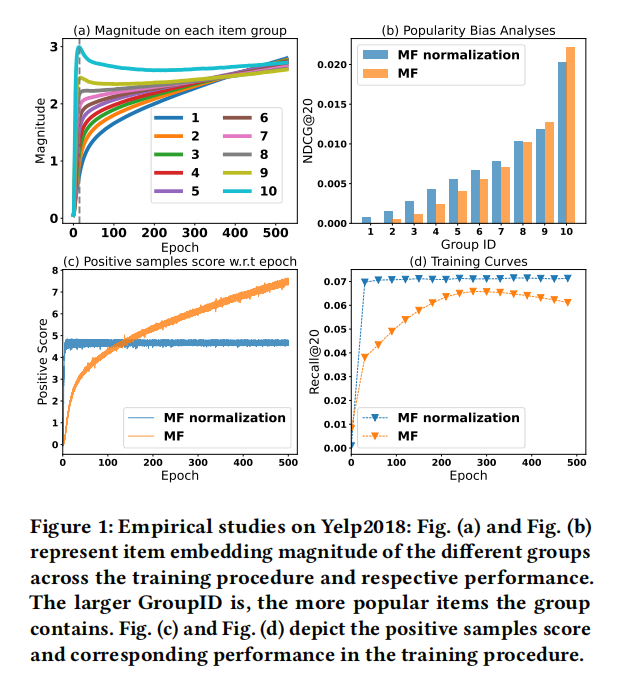
    • (1) 我们首先在训练过程中可视化不同项目受欢迎程度的项目嵌入的幅度（图1 a）。在这里，我们根据项目的受欢迎程度将项目分为十组。较大的组ID表示该组包含更多流行的项目。
    • (2) 我们还报告了不同项目组的表现（图1 b）。
    • (3) 具有训练时期的积极实例的预测分数为如图1 c. 所示。
    • (4) 我们可视化了有无归一化的MF的性能（图1 d）。所有实验均在MF主干和Yelp2018 数据集上进行。
    • 类似的结果也可以在其他模型（如LightGCN）和数据集上观察到。实验设置的详细信息可参考第5.1节。
  • 自由变化的幅度加剧了人气偏见。如果我们关注于训练的早期阶段(图1 (a))，流行物品的数量迅速上升，这与理论证明相一致。因此，流行的项目容易获得更高的分数，因为大小直接有助于模型预测。此外，不同的大小也损害了用户嵌入的训练。用户嵌入的梯度可以写成：𝜕𝜕𝐿e𝑢=I𝑢，𝑖𝜕𝑓𝜕𝐿（𝑢，𝑖）e𝑖，其中规模较大的流行项目会发挥过度的贡献，并可能压倒来自他人的信号。这个模型会陷入有偏差的结果。图1：(b)提供了证据。这个模型会陷入有偏差的结果。可以看出，有归一化的模型比没有归一化的模型产生了更公平的结果。
  • 自由变化的幅度损害了收敛性。如果我们将注意力转向图1 ©中的训练结束时，我们观察到，即使有许多epoch（例如，500），香草MF的预测分数和嵌入幅度仍然处于上升而不是收敛的状态，而性能持续下降（图1 (d)）。但是当我们利用在MF中的规范化时，我们观察到令人印象深刻的改进——模型以更少的epoch（即20）快速收敛，并且在更多的epoch时表现稳定。
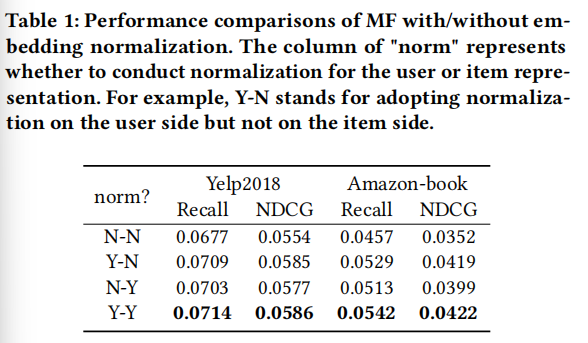
  • 规范化可以提高性能。为了进一步验证规范化的优点，在这里，我们直接测试了无论是否对用户或项目嵌入进行规范化时的推荐性能（表1）。可以看出，具有双边归一化的模型（即Y-Y)的性能明显优于具有单边归一化的模型（即Y-N或N-Y)，而且它们都超过了未进行归一化的模型（N-N）。

• 文章很枯燥，不想看了，屮。想看去自己看原文吧。