斐波那契数列的概念

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（LeonardodaFibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=0，F(1)=1,F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从 1963年起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

递归求解第N个斐波那契数

通过对斐波那契数的了解，我们很容易写出下面这个通项公式：

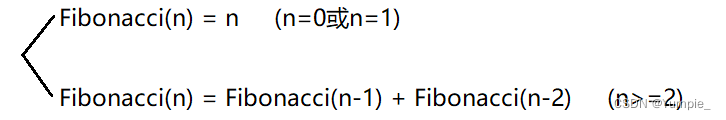
写出通项公式后用递归方法来实现就比较简单了：

long long Fibonacci(int n)
{
	if (n == 0 || n == 1)
		return n;
	else
		return Fibonacci(n - 1) + Fibonacci(n - 2);
}//递归

迭代求解第N个斐波那契数

迭代也就是我们通常所说的循环，即用循环的方法来求第n个斐波那契数：

long long Fibonacci(int n)
{
	if (n == 0)
		return 0;
	else if (n == 1)
		return 1;
	long long a = 0;
	long long b = 1;
	long long c = 1;
	while (n - 2)
	{
		a = b;
		b = c;
		c = a + b;
		n--;
	}
	return c;
}//迭代法

递归法和迭代法的比较

看到递归法与迭代法的实现之后，那么你认为哪一种方法比较好呢？

如果只看表面上的代码量，你可能以为递归法的实现更为简单，但在运行时，当你要求第50个斐波那契数的时候，递归法迟迟给不出运行结果，而迭代法不要说是求第50个斐波那契数，就算是求第100个，第1000个，第10000个斐波那契数，都是秒出结果。那这是什么原因呢？

其实，在递归法中，我们要求第50个斐波那契数，就要先求第49个和第48个斐波那契数，而要求第49个斐波那契数，又要先求第48个和第47个斐波那契数，要求第48个斐波那契数，就要先求第47个和第46个斐波那契数…

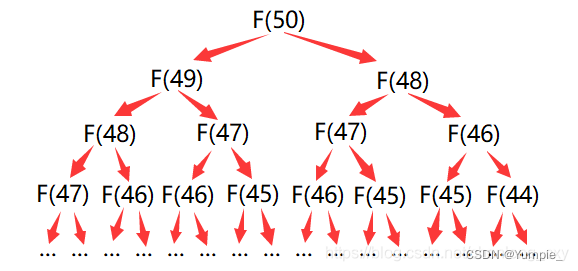
在图中我们可以看到，递归法中做了很多“无用功”，即对同一斐波那契数进行了多次求解。这里可以用一个代码来说明：

#include <stdio.h>
int count = 0;
long long Fibonacci(int n)
{
	if (n == 0)
		count++;
	if (n == 0 || n == 1)
		return n;
	else
		return Fibonacci(n - 1) + Fibonacci(n - 2);
}//递归
int main()
{
	Fibonacci(20);
	printf("%d\n", count);
	return 0;
}

这里我们要求第20个斐波那契数，我们用一个变量count来记录这个过程中Fibonacci(0)被执行的次数，结果惊人的发现：
在求第20个斐波那契数的过程中，我们仅仅对Fibonacci(0)就执行了4181次，更不用说还有Fibonacci(1)、Fibonacci(2)、Fibonacci(3)等等，而且这只是求第20个斐波那契数的过程就这样“艰难”了，更不用说求第50个斐波那契数的过程了。所以，用递归法计算第50个斐波那契数时出现迟迟没有结果的现象也是有原因的，因为计算机确实在努力计算了，只是做了太多重复计算。

而迭代法就不一样了，无论你求第几个斐波那契数，该函数只会调用一次，最主要的是：迭代法不会对同一个斐波那契数进行重复计算。

总结：

1.递归法虽然写法简单，但求解斐波那契数时会对同一斐波那契数进行多次计算，做了太多“无用功”。
2.迭代法虽然代码量相比递归法要多，但它对同一斐波那契数只会计算一次，避免了做“无用功”。