ZeroQuant-V2 LLM权重与激活量化

news2024/11/25 12:23:56

ref

ZeroQuant-V2: Exploring Post-training Quantization in LLMs from Comprehensive Study to Low Rank Compensation

4bit量化为什么重要

The case for 4-bit precision: k-bit Inference Scaling Laws

这篇文章研究表明4bit通常是最优的量化方法：同样的量化后模型大小情况下，4bit模型的精度更高。比特数越低，能够使能更大参数的模型，但是低比特导致量化精度损失也更大，相当于实现了最佳折中。同样大压缩后的模型，2倍参数量模型4bit压缩与1倍参数量模型8bit压缩的精度往往前者更高。

激活量化为什么重要

GPTQ等方法成功把模型参数压缩到4bit并得到广泛应用，但是该方法主要针对权重量化。当前比较缺乏有效的激活量化方法，很大因素是权重量化加上激活量化后会导致精度更大的损失。

但是缺乏激活量化，矩阵乘、卷积计算仍然需要float/half浮点计算，而且权重需要进行int到浮点的反量化，这导致性能较差，而且内存占用大。

ZeroQuant-V2的贡献

给出了一些比较有价值的洞察，并且给出了一个提升激活+权重量化精度的方法。

we undertake an exhaustive examination of the impact of PTQ on weight-only, activation-only, and combined weight-and-activation quantization. This investigation incorporates a range of PTQ methods, including round-to-nearest (RTN), GPTQ [12], ZeroQuant [36], and their respective variants. To broaden the scope of our analysis, we focus on two distinct model families, OPT [40] and BLOOM [28], spanning model sizes from 125M to a massive 176B.

In summary, we make the following contributions:
(1) We provide a thorough sensitivity analysis to demonstrate that a) Activation quantization is generally more sensitive to weight quantization; Smaller models usually have better activation quantization performance than the relative larger model. b) Different model families show different INT8 activation quantization behaviors; Particularly for large models, BLOOM-176B has small accuracy drops (about 1 perplexity or PPL) but OPT-30B and -66B experience worse performance.

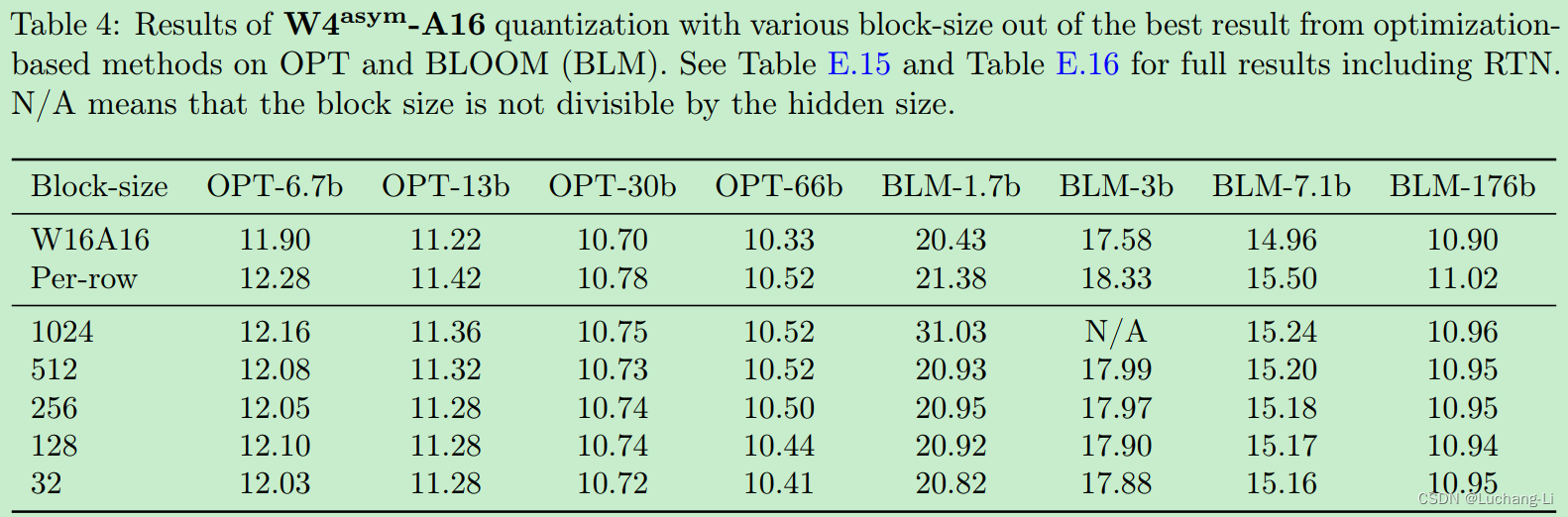
(2) We carry out a detailed evaluation and comparison of current PTQ methods, utilizing optimal configurations to maximize model size reduction while minimizing accuracy impact. We found that the current existing method can barely achieve less than 0.1 PPL points degradation for quantization with either INT4-weight or INT4-weight-and-INT8-activation (W4A8). To recover the 0.1 PPL, we strive to push the boundaries of employing fine-grained quantization (FGQ) techniques. We observe FGQ is able to recovered points degradation of <0.1 PPL for large models (>13B) for INT4 weight quantization, but there are still non-negligible model quality drops.

(3) Based on the above understanding, we further optimize existing methods and introduce a technique called Low Rank Compensation (LoRC), which employs low-rank matrix factorization on the quantization error matrix. Complementary to FGQ, LoRC plays a crucial role in enhancing the full model quality recovery, while there is little increase of the model size.

using LoRC on top of PTQ methods from [36, 12] and fine-grained quantization, we set a new quantization Pareto frontier for LLMs.
Meanwhile, we recommend the following setting for quantizing LLMs with LoRC (Note that activation quantization should be only applied if necessary):

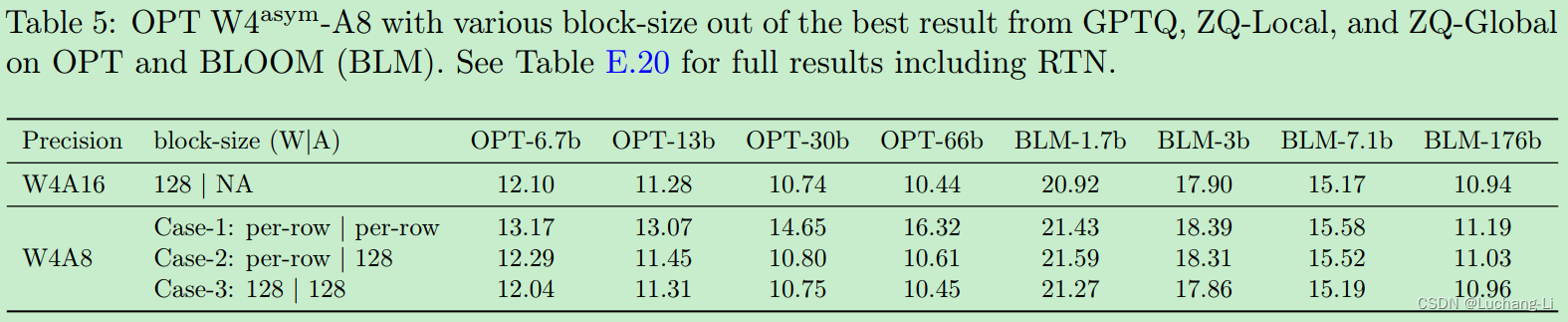
(1) For larger models (>10B), fine-grained (block size 64–256) 4-bit weight quantization plus 8-bit activation quantization (block size 64–256) with PTQ can be used for real deployment;

(2) For middle-size models (<10B and >1B), per-row INT8 quantization plus fine-grained (block size 64–256) INT8 activation quantization can be used with PTQ from [12, 36];

(3) For smaller models (<1B), per-row W8A8 (INT8 weight and INT8 activation) RTN is enough based on [36].

We employ both symmetric and asymmetric quantization to gauge the quantization sensitivity and highlight the advantage of asymmetric quantization.

Particularly, we implement per-row quantization [12] for weight quantization and per-token quantization for activation [36].

Robustness of Weight-only Quantization for Large Models.

INT8 weight-only quantization, either symmetric or asymmetric, results in negligible accuracy loss (less than 0.05, i.e., Class-1).
For INT4 quantization, the asymmetric method outperforms the symmetric approach in accuracy, attributable to its superior utilization of the quantization range. Interestingly, larger models exhibit better tolerance to low-precision quantization (i.e., INT4) than smaller models, with a few exceptions such as OPT-66B.

Challenge Encountered in Activation Quantization for Large Models.

Activation quantization has consistently proven more difficult than weight quantization
When compared to weight-only quantization, activation-only quantization indicates that asymmetric quantization can significantly improved performance over symmetric quantization. Moreover, contrary to weight-only quantization, smaller models typically exhibit better tolerance to activation quantization, as their hidden dimension is smaller and the activation dynamic range is also narrower than larger models [36].

existing quantization methods optimally harnessing the potential to minimize LLMs sizes

Fine-grained Quantization and Its Evaluation
finer-grained quantization schemes [5], where every k elements possess their own scaling factor and/or zero point.
For models of considerable size, specifically those equal to or exceeding 1B, the application of such fine-grained activation quantization (Case-1) results in a substantial reduction in quantization error compared to per-row activation (Case-2). By implementing fine-grained activation quantization with weight quantization (Case-3), we are able to almost restore the performance to the level of their W4A16 counterparts.
A trend of superior accuracy is observed with smaller block sizes in contrast to larger ones. However, the enhancement in performance reaches a saturation point when the size smaller or equal to 256, which corresponds to the range of values INT8 can represent. Despite INT8’s capability to signify 256 distinct values, activation quantization errors persist due to the application of uniform quantization.

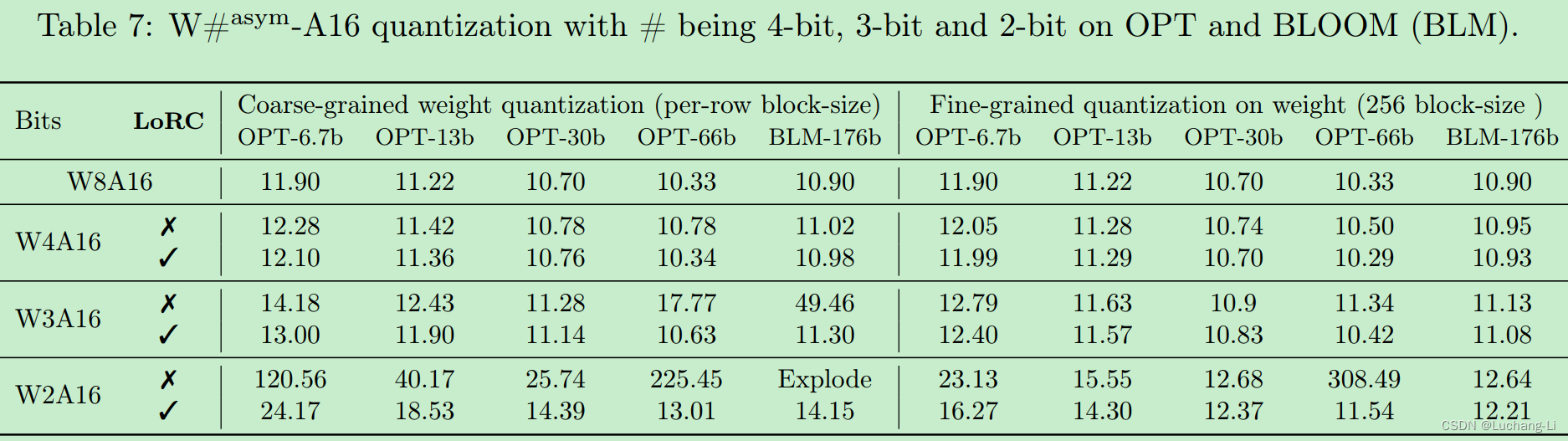
LoRC (Low Rank Compensation)

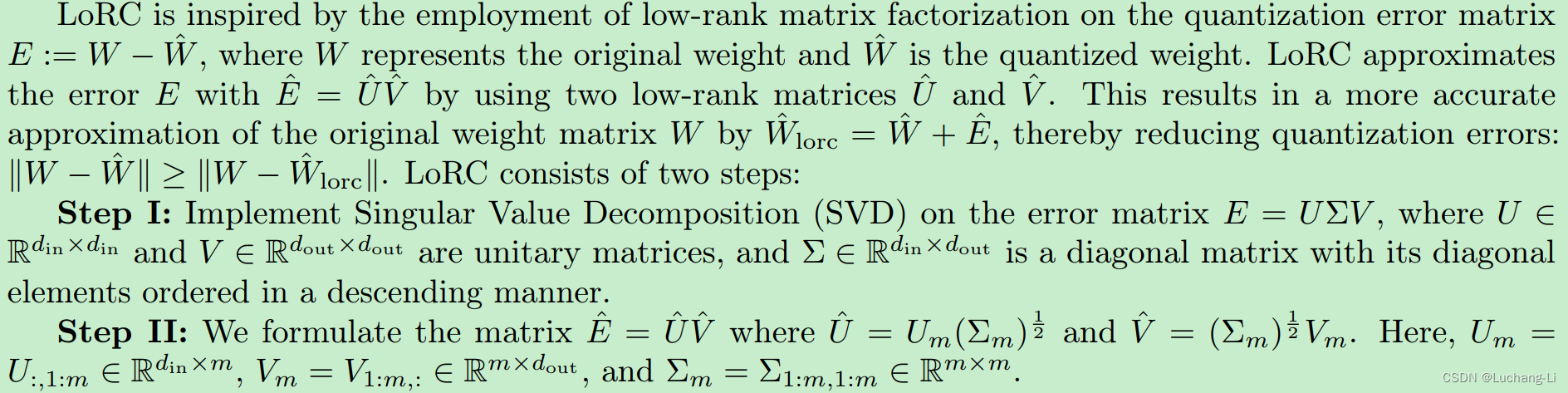
LoRC can be viewed as a supplementary feature to existing quantization methodologies such as RTN, GPTQ, and ZeroQuant-Local/Global, and can be seamlessly integrated with FGQ.
low-rank dimension m can be as small as 4 or 8
the two low-rank matrices, Uˆ and Vˆ , can be quantized to 8-bit without any performance discrepancy

the combination of fine-grained quantization with LoRC yields the most impressive results, underscoring the efficacy of LoRC when integrated with FGQ. Overall, the results emphasize the benefits of using LoRC for enhanced performance in weight quantization and its compatibility with FGQ. Notably, recovering the last 0.05-0.1 perplexity can be challenging, but with LoRC, we are able to nearly recover the original model quality for INT4 quantization.

这个U V计算得到后又怎么用？这个细节文章并没有讲！

只提到