0 写在前面

机器学习强基计划聚焦深度和广度，加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理；“广”在分析多个机器学习模型：决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。强基计划实现从理论到实践的全面覆盖，由本人亲自从底层编写、测试与文章配套的各个经典算法，不依赖于现有库，可以大大加深对算法的理解。

🚀详情：机器学习强基计划(附几十种经典模型源码)

---

1 字典学习

人类社会一切已发现或未发现的知识都必须通过字、词、句进行表示，而整体的知识量非常庞大——人类每天产生的新知识约2T；换言之，无论人类的知识多么浩瀚，一本新华字典或牛津字典也足以表达人类从古至今乃至未来的所有知识——字典中字、词、句的排列组合。所以字典相当于庞大数据集的一种降维表示，且蕴藏样本背后最本质的特征。现代神经科学表明，哺乳动物大脑的初级视觉皮层主要工作就是进行图像的字典表示。

考虑样本矩阵的一种分解

$$\mathbf{X}=\mathbf{DA}$$

其中$\mathbf{X}=\left[\begin{array}{cccc}{\mathbf{x}}_1& {\mathbf{x}}_2& \cdots & {\mathbf{x}}_m\end{array}\right]\in {\mathbb{R}}^{d\times m}$是样本矩阵；$\mathbf{A}=\left[\begin{array}{cccc}{\mathbf{\alpha }}_1& {\mathbf{\alpha }}_2& \cdots & {\mathbf{\alpha }}_m\end{array}\right]\in {\mathbb{R}}^{k\times m}$是样本$\mathbf{X}$的编码矩阵，其中${\mathbf{\alpha }}_i$是${\mathbf{x}}_i$的编码；$\mathbf{D}=\left[\begin{array}{cccc}{\mathbf{d}}_1& {\mathbf{d}}_2& \cdots & {\mathbf{d}}_k\end{array}\right]\in {\mathbb{R}}^{d\times k}$称为字典(dictionary)，${\mathbf{d}}_i$称为字典的一个原子(atom)，通常经过归一化处理，$k$称为字典的词汇量，可由用户指定。设样本相当于字典而言相当庞大，即$m\gg k$

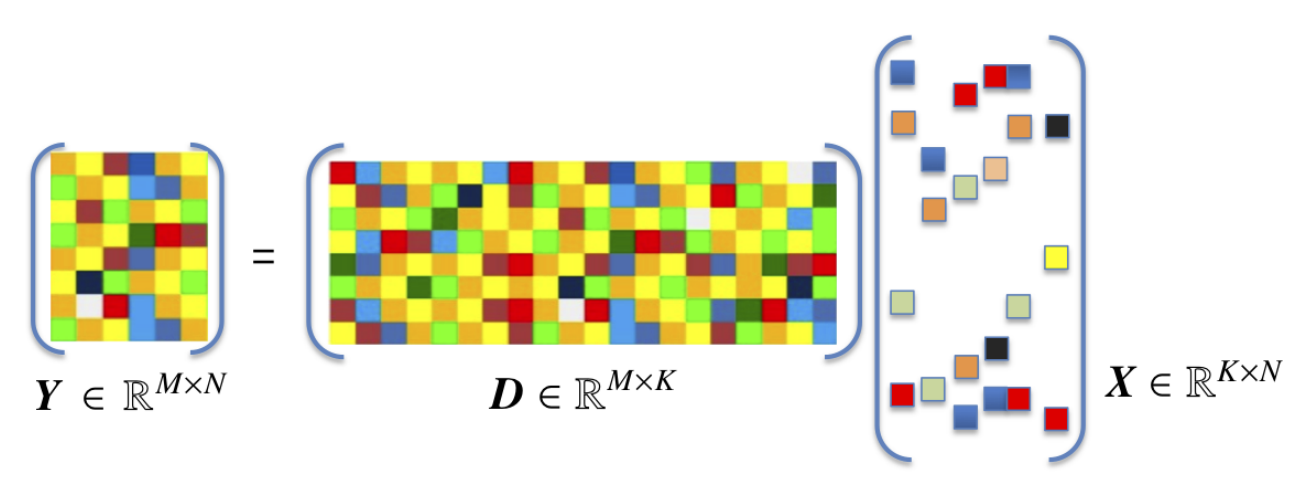
考察样本的编码形式：

• 若$k<d$，则$\mathbf{D}$称为欠完备字典，相当于特征选择或线性降维技术；
• 若$k>d$，则$\mathbf{D}$称为过完备字典，编码维度增大似乎违背了避免维数灾难的原则，但此时约束${\mathbf{\alpha }}_i$是${\mathbf{x}}_i$的稀疏表示(sparse representation)——含有大量零元素。

2 稀疏表示与稀疏编码

类比真实的《现代汉语字典》，其中约有3500个常用字，而一篇文档可能只使用了其中15%的字，若将每个文档看作一个样本，每个字作为一个特征，字在文档中出现的频率作为特征取值，那么一篇文档的特征向量约有85%的零元素。但不同主题的文档使用的主要词汇可能相差很大(比如古风诗词和科幻小说)，导致稀疏分布不同

因此稀疏表示不会掩盖真实特征，相反，甚至可能使困难的学习问题变得线性可分，而且得益于计算机科学对稀疏矩阵的研究，稀疏化使机器学习在计算和存储方面更高效

那这里稠密和稀疏的概念与维数灾难有什么关系呢？

机器学习任务中通常面临高维特征空间，若特征维数为40，则要实现密采样就需要$10^{80}$个样本——相当于宇宙中基本粒子的总数。所以密采样在高维特征空间中无法实现，换言之，高维特征样本分布非常稀疏，给机器学习训练、算法采样优化带来了困难。这种高维情形下机器学习任务产生严重障碍现象称为维数灾难(curse of dimensionality)，维数灾难还会以指数级的规模造成计算复杂度上升、存储占用大等问题，具体可见机器学习强基计划8-1：图解主成分分析PCA算法(附Python实现)

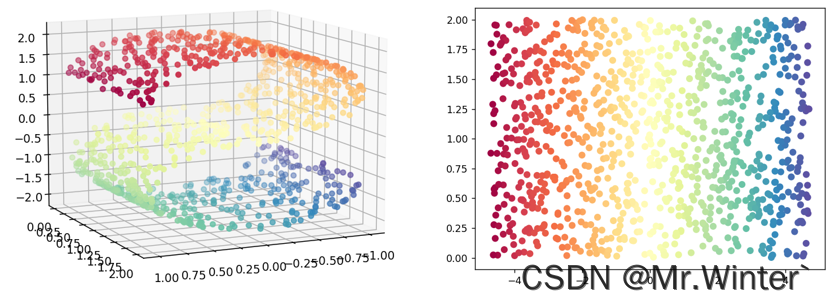
所以本节研究的对象是特征的稠密与稀疏，而维数灾难里讨论的是特征空间中样本的稠密与稀疏

稀疏编码(sparse coding)研究给定字典时如何用尽量稀疏的表示还原样本，形式化为

$${\mathbf{\alpha }}_i^{\ast }=\arg \underset{{\mathbf{\alpha }}_i}{\min }{\Vert {\mathbf{x}}_i-{\mathbf{D\alpha }}_i\Vert }_2^2\mathrm{s}.\mathrm{t}.{\Vert {\mathbf{\alpha }}_i\Vert }_0⩽L$$

必须指出，${\Vert {\mathbf{\alpha }}_i\Vert }_0$的存在导致该优化是NP难问题。由于每个样本的稀疏编码相互独立，故优化过程可并行进行。可以证明，当${\mathbf{\alpha }}_i$充分稀疏时，上述优化问题有唯一解，且和

$${\mathbf{\alpha }}_i^{\ast }=\arg \underset{{\mathbf{\alpha }}_i}{\min }{\Vert {\mathbf{x}}_i-{\mathbf{D\alpha }}_i\Vert }_2^2+\lambda {\Vert {\mathbf{\alpha }}_i\Vert }_1$$

同解，此时可采用PGD等凸优化技术求解。然而因为不能保证${\mathbf{\alpha }}_i$充分稀疏，即非凸优化与凸优化的求解不一定等价，因此本节介绍基于贪心策略的非凸优化求解方法

3 匹配追踪MP算法

匹配追踪(Matching Pursuit, MP)的核心思想是挑选少数几个影响力最大的字典原子重构原始样本，其余字典原子置零，在稀疏化的同时保证主要信息不丢失。MP采用样本在字典原子方向的投影绝对值衡量影响力，其原理类似余弦相似度

$$h\left({\mathbf{d}}_i,\mathbf{r}\right)=\left|\frac{⟨{\mathbf{d}}_i,\mathbf{r}⟩}{\left|{\mathbf{d}}_i\right|}\right|$$

其中$\mathbf{r}$为残差(residual)或重构误差，衡量了基于稀疏表示的样本与原始样本间的误差。初始时刻$\mathbf{r}=\mathbf{x}$，当字典原子单位化后，贪心策略要求选择满足

$$i^{\ast }=\arg \underset{i}{\max }\left|⟨{\mathbf{d}}_i,\mathbf{r}⟩\right|$$

的字典原子并用相应影响力更新编码向量，更新后的稀疏表示应比前几轮迭代更逼近原始样本，所以当重构误差小于阈值时即得最优的稀疏表示。如图所示为算法示意图，直观地，残差不断减小。

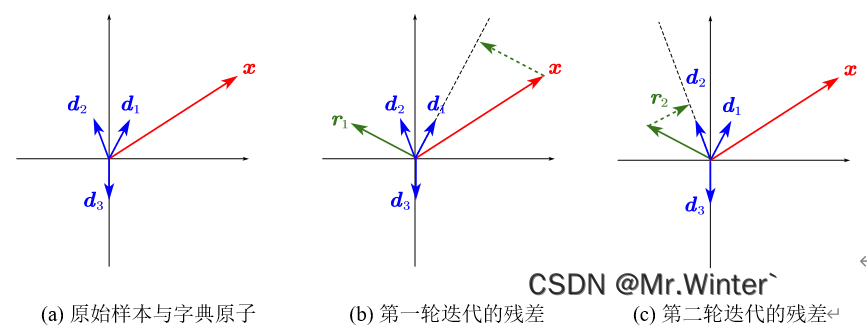
算法流程如下所示

4 正交匹配追踪OMP算法

MP算法的缺陷在于残差只与本轮迭代选择的字典原子正交，即同一字典原子可能在迭代中被重复选择，例如上图第二轮迭代后的残差${\mathbf{r}}_2$与${\mathbf{d}}_1$夹角最小，导致${\mathbf{d}}_1$被再次选择。若MP中对同一字典原子的选择可以合并为一次，即每次循环中都选择不同的原子，则可以大大减少迭代次数。正交匹配追踪(Orthogonal Matching Pursuit, OMP)通过引入正交性质克服了MP算法收敛速度慢的缺陷，改进算法如表所示

与MP算法最大的区别在于最小二乘编码的计算，使得

$${\mathbf{D}}_{\Gamma }^T\mathbf{r}={\mathbf{D}}_{\Gamma }^T\left(\mathbf{x}-{\mathbf{D}}_{\Gamma }{\mathbf{\alpha }}_{\Gamma }^{\ast }\right)=0$$

即残差与字典原子正交，保证了更新的效率。采用最小二乘法而非施密特正交化的原因是对整个字典正交化的计算复杂度太高，且造成计算浪费(未被选择的原子也被正交化)

完整代码通过下方名片联系博主获取

---

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇