【元胞自动机】格子波尔兹曼模型及其应用研究（Matlab代码实现）

news2024/11/22 10:31:50

👨‍🎓个人主页：研学社的博客

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🌈3 Matlab代码实现

🎉4 参考文献

💥1 概述

格子波尔兹曼模型（Lattice Boltzmann Model,LBM）是近年来兴起的一种求解偏微分方程的数值工具。目前,LBM在流体力学领域中的应用已经和传统的数值方法并驾齐驱,得到了国际上的广泛关注。LBM和传统的求解偏微分方程的数值方法的区别在于其出发点是系统的微观模型,使LBM的宏观方程与偏微分方程保持一致,并在对系统进行模拟的同时,实现对偏微分方程的求解。虽然目前LBM在图像处理领域中的应用鲜有报道,但实际上LBM在图像处理领域有着很大的应用潜力。首先,从上世纪六十年代开始,作为LBM发展前身的传统元胞自动机在图像处理领域中就已经得到广泛应用。其次,LBM继承了传统元胞自动机方法在图像处理中的优点,如算法实现简单,计算并行度高,模型稳定性好。再次,LBM是一个非常有效的数值工具,在流体力学中它被广泛用来求解各种偏微分方程。借鉴基于偏微分方程理论的图像处理模型与方法,利用LBM求解偏微分方程,可以实现包括图像去噪,图像边缘检测和图像分割在内的各种图像处理。

📚2 运行结果

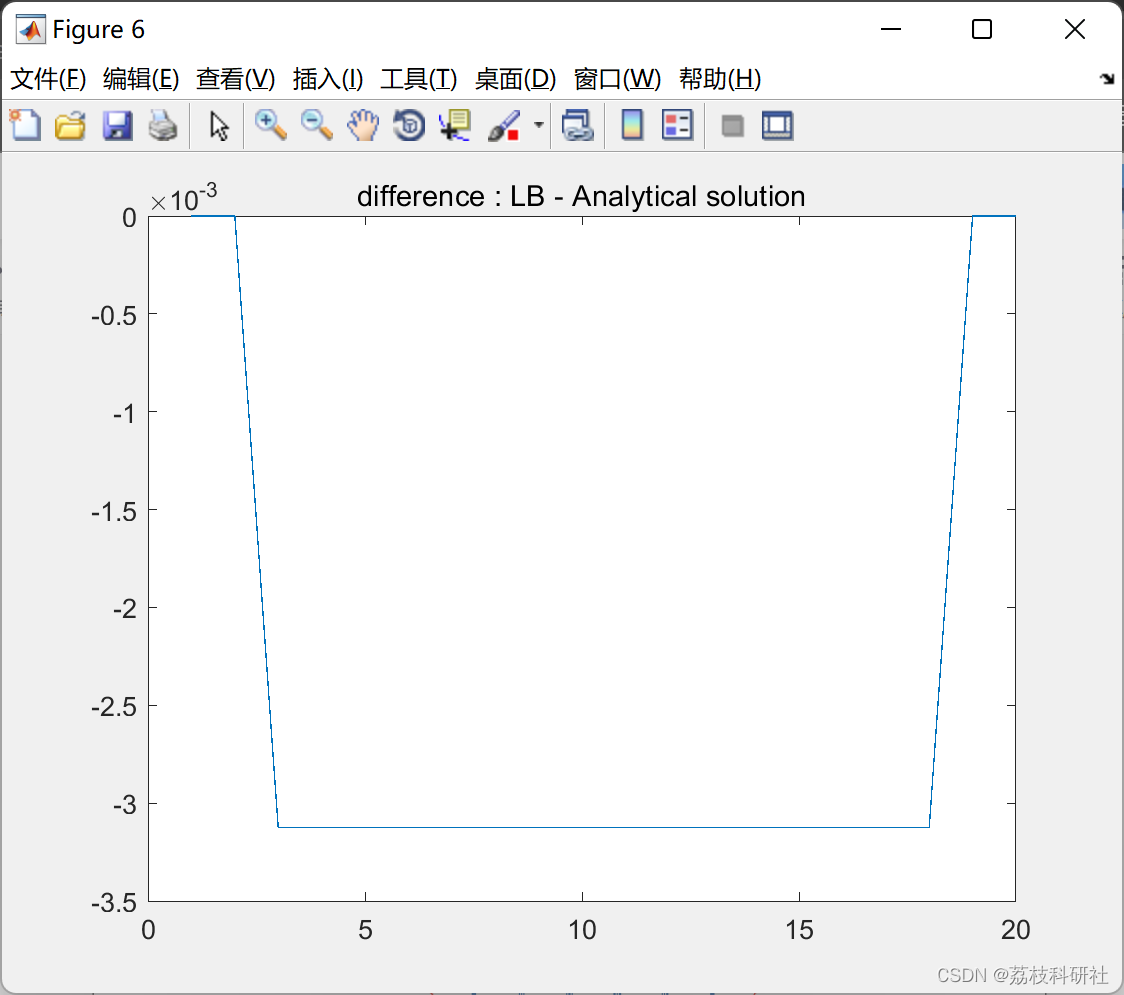
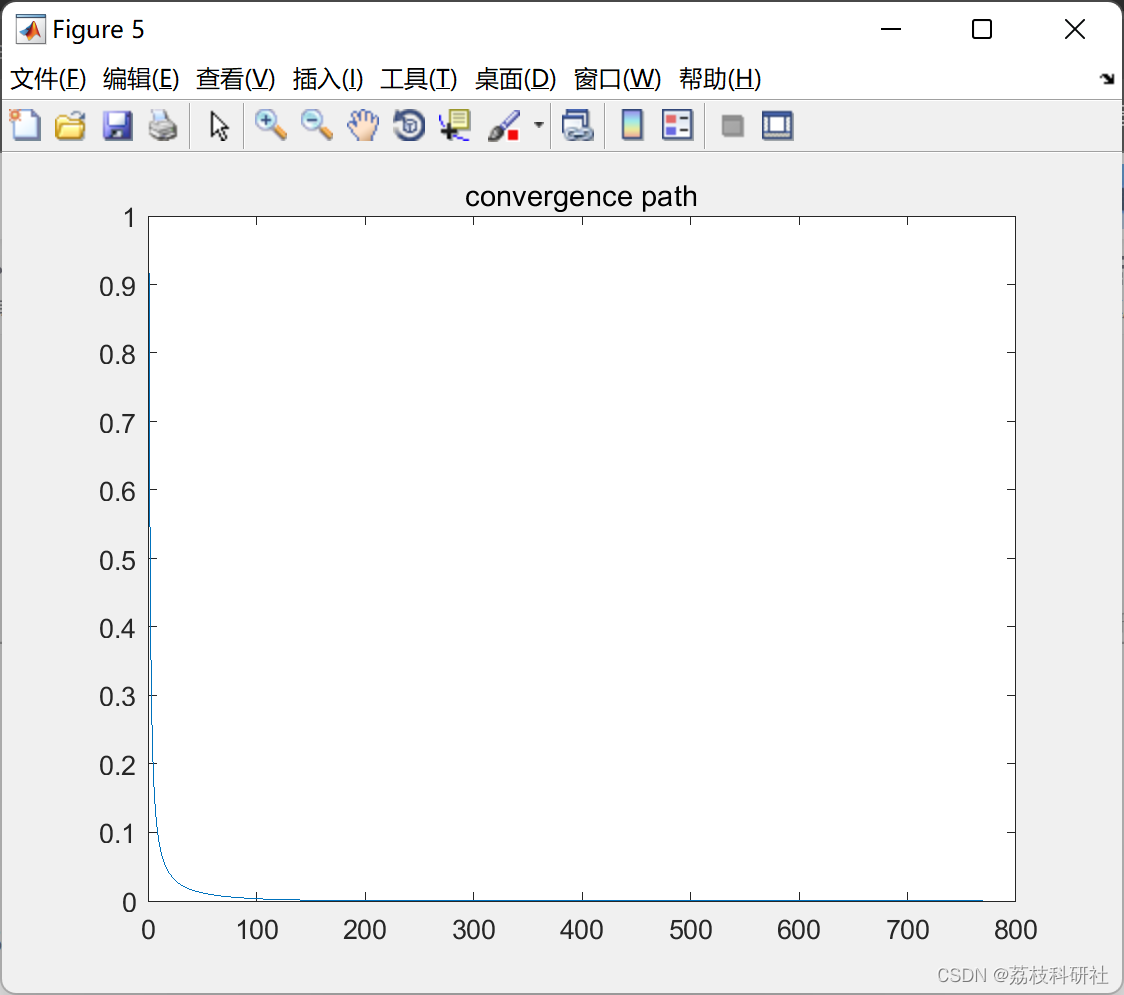
部分代码：

% Pores in 2D : Wet and Dry locations (Wet ==1 , Dry ==0 )
wXh_Dry=[3,1];wXh_Wet=[3,4];

if obs_regolare, % with internal obstacles

A=repmat([zeros(wXh_Dry),ones(wXh_Wet)],[1,3]);A=[A,zeros(wXh_Dry)];
B=ones(size(A));
C=[A;B] ; D=repmat(C,4,1);
D=[B;D]
end

if obs_irregolare, % with int obstacles
A1=repmat([zeros(wXh_Dry),ones(wXh_Wet)],[1,3]);
A1=[A1,zeros(wXh_Dry)] ;
B=ones(size(A1));
C1=repmat([ones(wXh_Wet),zeros(wXh_Dry)],[1,3]); C1=[C1,ones(wXh_Dry)];
E=[A1;B;C1;B];
D=repmat(E,2,1);
D=[B;D]
end

if ~Pois_test
figure,imshow(D,[])
Channel2D=D;
Len_Channel_2D=size(Channel2D,1); % Length
Width=size(Channel2D,2); % should not be hod
Channel_2D_half_Width=Width/2,
end

% test without obstacles (i.e. 2D channel & no obstacles)

if Pois_test
%over-writes the definition of the pore space
clear Channel2D
Len_Channel_2D=36, % lunghezza canale 2d
Channel_2D_half_Width=8; Width=Channel_2D_half_Width*2;
Channel2D=ones(Len_Channel_2D,Width); % define wet area
%Channel2D(6:12,6:8)=0; % put fluid obstacle
imshow(Channel2D,[]);
end

[Nr Mc]=size(Channel2D); % Number rows and Munber columns

% porosity
porosity=nnz(Channel2D==1)/(Nr*Mc)

% FLUID PROPERTIES
% physical properties
cs2=1/3; %
cP_visco=0.5; % [cP] 1 CP Dinamic water viscosity 20 C
density=1.; % fluid density
Lky_visco=cP_visco/density; % lattice kinematic viscosity
omega=(Lky_visco/cs2+0.5).^-1; % omega: relaxation frequency
%Lky_visco=cs2*(1/omega - 0.5) , % lattice kinematic viscosity
%dPdL= Pressure / dL;% External pressure gradient [atm/cm]

uy_fin_max=-0.2;
%dPdL = abs( 2*Lky_visco*uy_fin_max/(Channel_2D_half_Width.^2) );
dPdL=-0.0125;
uy_fin_max=dPdL*(Channel_2D_half_Width.^2)/(2*Lky_visco); % Poiseuille Gradient;
% max poiseuille final velocity on the flow profile
uy0=-0.001; ux0=0.0001; % linear vel .. inizialization

%
% uy_fin_max=-0.2; % max poiseuille final velocity on the flow profile
% omega=0.5, cs2=1/3; % omega: relaxation frequency
% Lky_visco=cs2*(1/omega - 0.5) , % lattice kinematic viscosity
% dPdL = abs( 2*Lky_visco*uy_fin_max/(Channel_2D_half_Width.^2) ); % Poiseuille Gradient;
%

uyf_av=uy_fin_max*(2/3);; % average fluid velocity on the profile

x_profile=([-Channel_2D_half_Width:+Channel_2D_half_Width-1]+0.5);
uy_analy_profile=uy_fin_max.*(1- ( x_profile /Channel_2D_half_Width).^2 ); % analytical velocity profile

av_vel_t=1.e+10; % inizialization (t=0)
%PixelSize= 5; % [Microns]
%dL=(Nr*PixelSize*1.0E-4); % sample hight [cm]

%
% EXPERIMENTAL SET-UP
% inlet and outlet buffers
inb=2, oub=2; % inlet and outlet buffers thickness
% add fluid at the inlet (top) and outlet (down)
inlet=ones(inb,Mc); outlet=ones(oub,Mc);
Channel2D=[ [inlet]; Channel2D ;[outlet] ] ; % add flux in and down (E to W)