Letbook Cookbook题单——数组二分与双指针

1. 两数之和

难度：简单

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那两个整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

提示：

2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案

**进阶：**你可以想出一个时间复杂度小于 O(n2) 的算法吗？

暴力

两重循环

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
    for (int i = 0; i < numsSize; ++i) {
        for (int j = i + 1; j < numsSize; ++j) {
            if (nums[i] + nums[j] == target) {
                int* ret = malloc(sizeof(int) * 2);
                ret[0] = i, ret[1] = j;
                *returnSize = 2;
                return ret;
            }
        }
    }
    *returnSize = 0;
    return NULL;
}

哈希表

这题原来想用双指针，但是后面仔细想了下，如果双指针要存储下标就要开结构体，然后对结构体根据元素大小排序，再双指针，还是比较麻烦，最后还是hash好

用一个map，键为元素大小，值为下标

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int>mp;
        for(int i=0;i<nums.size();i++)
        {
        if(mp.find(target-nums[i])!=mp.end())
        return {mp[target-nums[i]],i};
          mp[nums[i]]=i;
        }
        return {};
    }
};

4. 寻找两个正序数组的中位数

难度：困难

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

提示：

nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106

直接去题解区看题解吧，边界问题太复杂。脑子：我会了！手：？？？写了一会后，脑子：？？？反正就是懂了后代码写的又臭又长

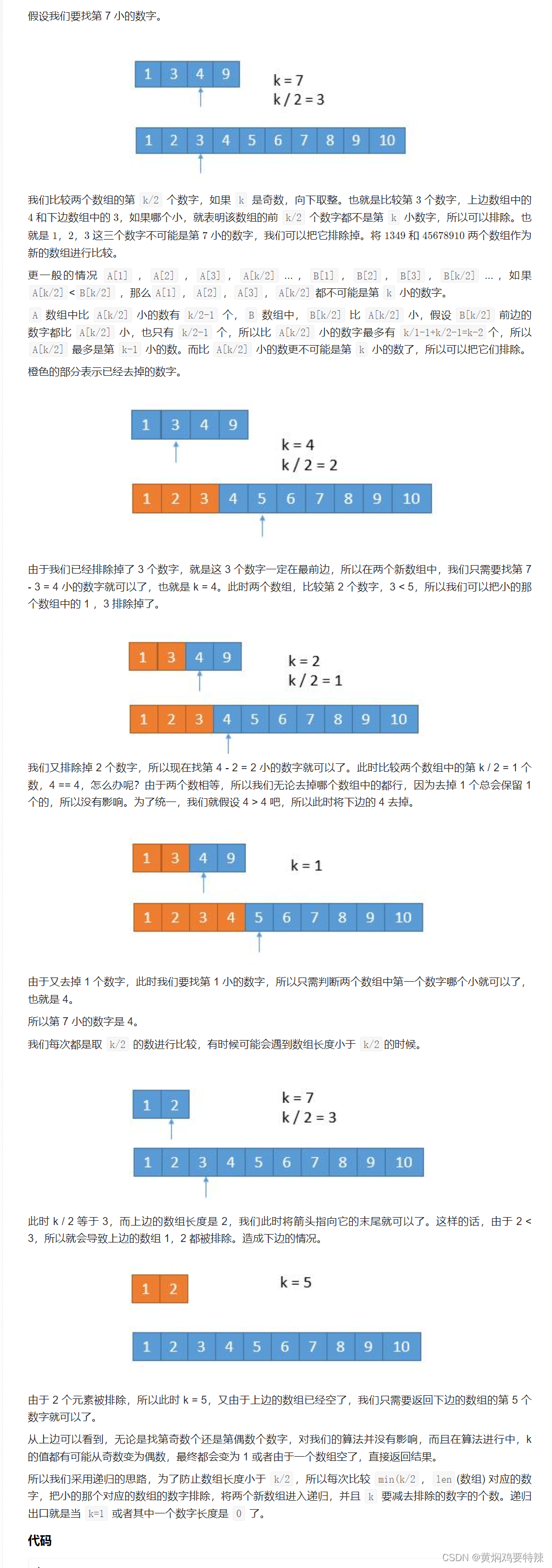
这里分享一个自认为最容易理解的解法——第k小数解法

第k小数解法

在这里插入图片描述

class Solution {
public:
    int getKthElement(const vector<int>& nums1, const vector<int>& nums2, int k) {
        /* 主要思路：要找到第 k (k>1) 小的元素，那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
         * 这里的 "/" 表示整除
         * nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
         * nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
         * 取 pivot = min(pivot1, pivot2)，两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
         * 这样 pivot 本身最大也只能是第 k-1 小的元素
         * 如果 pivot = pivot1，那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums1 数组
         * 如果 pivot = pivot2，那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums2 数组
         * 由于我们 "删除" 了一些元素（这些元素都比第 k 小的元素要小），因此需要修改 k 的值，减去删除的数的个数
         */

        int m = nums1.size();
        int n = nums2.size();
        int index1 = 0, index2 = 0;

        while (true) {
            // 边界情况
            if (index1 == m) {
                return nums2[index2 + k - 1];
            }
            if (index2 == n) {
                return nums1[index1 + k - 1];
            }
            if (k == 1) {
                return min(nums1[index1], nums2[index2]);
            }

            // 正常情况
            int newIndex1 = min(index1 + k / 2 - 1, m - 1);
            int newIndex2 = min(index2 + k / 2 - 1, n - 1);
            int pivot1 = nums1[newIndex1];
            int pivot2 = nums2[newIndex2];
            if (pivot1 <= pivot2) {
                k -= newIndex1 - index1 + 1;
                index1 = newIndex1 + 1;
            }
            else {
                k -= newIndex2 - index2 + 1;
                index2 = newIndex2 + 1;
            }
        }
    }

    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int totalLength = nums1.size() + nums2.size();
        if (totalLength % 2 == 1) {
            return getKthElement(nums1, nums2, (totalLength + 1) / 2);
        }
        else {
            return (getKthElement(nums1, nums2, totalLength / 2) + getKthElement(nums1, nums2, totalLength / 2 + 1)) / 2.0;
        }
    }
};

11. 盛最多水的容器

难度中等

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

**说明：**你不能倾斜容器。

示例 1：

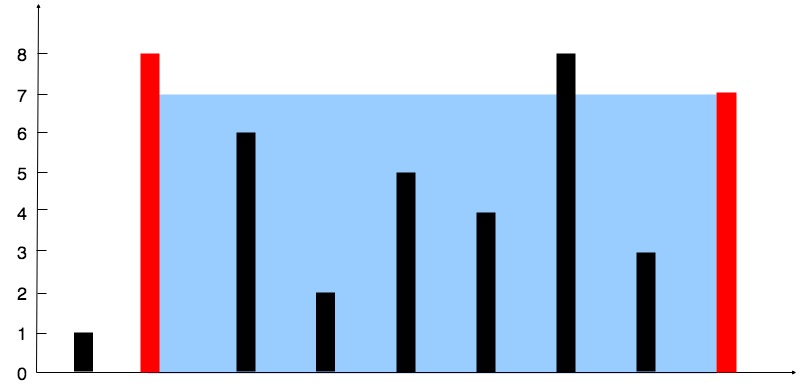
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

n == height.length
2 <= n <= 105
0 <= height[i] <= 104

贪心+双指针

面积为 min(h[a], h[b]) * (b - a)，双指针应该移动哪个呢？h[a] 和 h[b] 二者必然有长边和短边，则若短边向中间靠拢，则有可能因短边边长，而使面积变大，但若长边向中间靠拢，则一定会让面积变小，因此，应将短边向中间靠拢

class Solution {
public:
    int maxArea(vector<int>& h) {
        int ans=0;
        int l=0,r=h.size()-1;
        while(l<r)
        {
            ans=max(min(h[l],h[r])*(r-l),ans);
            if(h[l]<=h[r])
            l++;
            else
            r--;
        }
        return ans;
    }
};

15. 三数之和

难度中等

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

**注意：**答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

提示：

3 <= nums.length <= 3000
-105 <= nums[i] <= 105

双指针+去重

先对数组进行排序，然后固定一个元素a，在其后面的位置寻找和为target-a的两个元素，因为数组已经排好序了，所以我们可以用双指针优化为n，但是要注意去重的问题，最简单的是使用map，但那显得太没水平了。只要判断每个元素前面一个是否和它相等的就行了，如果相等就没必要选了，因为之前选择的时候已经过它了

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>>ans;
        sort(nums.begin(),nums.end());
        for(int i=0;i<nums.size()-1;i++)
        {
            if(i==0||nums[i]!=nums[i-1])
            {
            int l=i+1,r=nums.size()-1;
            while(l<r)
            {
                if(nums[l]+nums[r]+nums[i]==0)
                {
                ans.push_back({nums[i],nums[l],nums[r]});
                l++,r--;
                while(l<nums.size()&&nums[l-1]==nums[l])
                l++;
                while(r>i&&nums[r]==nums[r+1])
                r--;
                }
                else if(nums[r]+nums[l]+nums[i]>0)
                r--;
                else
                l++;
            }
            }
        }
        return ans;
    }
};

16. 最接近的三数之和

难度中等1300收藏分享切换为英文接收动态反馈

给你一个长度为 n 的整数数组 nums 和一个目标值 target。请你从 nums 中选出三个整数，使它们的和与 target 最接近。

返回这三个数的和。

假定每组输入只存在恰好一个解。

示例 1：

输入：nums = [-1,2,1,-4], target = 1
输出：2
解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。

示例 2：

输入：nums = [0,0,0], target = 1
输出：0

提示：

3 <= nums.length <= 1000
-1000 <= nums[i] <= 1000
-104 <= target <= 104

双指针

和15题有点类似，只不过变成了最接近的和

用两个指针i和j。先对数组进行排序，i 从头开始往后面扫。这里同样需要注意数组中存在多个重复数字的问题。具体处理方法很多，可以用 map 计数去重。i 在循环的时候和前一个数进行比较，如果相等，i 继续往后移，直到移到下一个和前一个数字不同的位置。j，k 两个指针开始一前一后夹逼。j 为 i 的下一个数字，k 为数组最后一个数字，由于经过排序，所以 k 的数字最大。j 往后移动，k 往前移动，逐渐得出最接近 target 的值。

class Solution {
public:
    int threeSumClosest(vector<int>& nums, int target) {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        int ans = nums[0] + nums[1] + nums[2];
        for(int i = 0; i < n - 2; i ++)
        {
            int ll = i + 1, rr = n - 1;
            while(ll < rr)
            {
                int temp = nums[i] + nums[ll] + nums[rr];
                if(temp == target)
                    return target;
                else
                {
                    if(abs(temp - target) < abs(ans - target))
                        ans = temp;
                    if(temp > target)
                        rr --;
                    else
                        ll ++;
                }
            }
        }
        return ans;
    }
};

18. 四数之和

难度中等

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

0 <= a, b, c, d < n
a、b、c 和 d 互不相同
nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按 任意顺序 返回答案。

示例 1：

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：

输入：nums = [2,2,2,2,2], target = 8
输出：[[2,2,2,2]]

提示：

1 <= nums.length <= 200
-109 <= nums[i] <= 109
-109 <= target <= 109

和三数之和几乎一模一样了

双指针

using LL = long long;

class Solution {
public:
    // 思路：类比三数之和，先排序，然后枚举并固定a b，利用首尾指针寻找 c d
    vector<vector<int>> fourSum(vector<int>& nums, int x) {
        if(nums.size()<4)return {};
        vector<vector<int>> res;
        sort(nums.begin(),nums.end());
        for(int i=0;i<nums.size()-3;++i){
            // 由于nums[i]对应的元素值已经枚举过了，不需要再次枚举了
            if(i>0&&nums[i]==nums[i-1])continue;
            // 以下代码与 三数之和 一样
            for(int j=i+1;j<nums.size()-2;++j){
                // 由于nums[i]对应的元素值已经枚举过了，不需要再次枚举了
                if(j>i+1&&nums[j]==nums[j-1])continue;
                // 首尾指针来寻找c d
                int l=j+1,r=nums.size()-1;
                while(l<r){
                    LL sum=0LL+nums[i]+nums[j]+nums[r]+nums[l];
                    if(sum>x)r--;// sum太大，向左逼近
                    else if(sum<x)l++;// sum太小，向右逼近
                    else{
                        // 添加结果
                        res.push_back({nums[i],nums[j],nums[l],nums[r]});
                        // 缩小区间
                        l++,r--;
                        while(l<r&&nums[l]==nums[l-1])l++;
                        while(l<r&&nums[r]==nums[r+1])r--;
                    }
                }
            }
        }
        return res;
    }
};

26. 删除有序数组中的重复项

难度简单

给你一个 升序排列 的数组 nums ，请你原地删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持一致。

由于在某些语言中不能改变数组的长度，所以必须将结果放在数组nums的第一部分。更规范地说，如果在删除重复项之后有 k 个元素，那么 nums 的前 k 个元素应该保存最终结果。

将最终结果插入 nums 的前 k 个位置后返回 k 。

不要使用额外的空间，你必须在 原地修改输入数组 并在使用 O(1) 额外空间的条件下完成。

判题标准:

系统会用下面的代码来测试你的题解:

int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案

int k = removeDuplicates(nums); // 调用

assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
    assert nums[i] == expectedNums[i];
}

如果所有断言都通过，那么您的题解将被通过。

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

提示：

1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按升序排列

快慢指针

看到一个比较有趣的解释：

可以看作一个喜新厌旧的人的一个排队列过程。这个人比较喜新厌旧，看到没有见过的数字，就把它按顺序从左到右排好，如果是已经见过的数字就直接忽略掉。比如0 4 4 7 7 7 9 第一个数字保持不动。然后往后面看看到第一个4，没见过，是第一次看到4，于是把它排到0的后面。再往后看，又看到一个数字4，老面孔直接忽略掉。再往后看看到一个数字7，是新面孔。于是把她拉到最左边，放在紧跟着0 4的位置。再往后看是7，直接忽略，接着又是7，直接忽略。直到看到新的数字9，然后把然后把放到0 4 7的后面。可以理解为左边是所有的新面孔的队列，而快指针就是评审官，负责找到新面孔。

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int n = nums.size();
        if (n == 0) {
            return 0;
        }
        int fast = 1, slow = 1;
        while (fast < n) {
            if (nums[fast] != nums[fast - 1]) {
                nums[slow] = nums[fast];
                ++slow;
            }
            ++fast;
        }
        return slow;
    }
};

27. 移除元素

难度简单1586收藏分享切换为英文接收动态反馈

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

说明:

为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以**「引用」**方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参作任何拷贝
int len = removeElement(nums, val);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3]
解释：函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。

提示：

0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100

双指针

和上面一个题差不多

这里数组的删除并不是真的删除，只是将删除的元素移动到数组后面的空间内，然后返回数组实际剩余的元素个数，最终判断题目的时候会读取数组剩余个数的元素进行输出

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
      int low=-1,fast=0,len=nums.size();
      while(fast<len)
      {
          if(nums[fast]!=val)
          {
              swap(nums[++low],nums[fast]);
          }
          fast++;
      }
      return low+1;
    }
};

33. 搜索旋转排序数组

难度中等

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

提示：

1 <= nums.length <= 5000
-104 <= nums[i] <= 104
nums 中的每个值都 独一无二
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-104 <= target <= 104

很有意思的二分查找

二分查找

题目要求 O(logN)O(logN) 的时间复杂度，基本可以断定本题是需要使用二分查找，怎么分是关键。
由于题目说数字了无重复，举个例子：
1 2 3 4 5 6 7 可以大致分为两类，
第一类 2 3 4 5 6 7 1 这种，也就是 nums[start] <= nums[mid]。此例子中就是 2 <= 5。
这种情况下，前半部分有序。因此如果 nums[start] <=target<nums[mid]，则在前半部分找，否则去后半部分找。
第二类 6 7 1 2 3 4 5 这种，也就是 nums[start] > nums[mid]。此例子中就是 6 > 2。
这种情况下，后半部分有序。因此如果 nums[mid] <target<=nums[end]，则在后半部分找，否则去前半部分找。

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int n = (int)nums.size();
        if (!n) {
            return -1;
        }
        if (n == 1) {
            return nums[0] == target ? 0 : -1;
        }
        int l = 0, r = n - 1;
        while (l <= r) {
            int mid = (l + r) / 2;
            if (nums[mid] == target) return mid;
            if (nums[0] <= nums[mid]) {
                if (nums[0] <= target && target < nums[mid]) {
                    r = mid - 1;
                } else {
                    l = mid + 1;
                }
            } else {
                if (nums[mid] < target && target <= nums[n - 1]) {
                    l = mid + 1;
                } else {
                    r = mid - 1;
                }
            }
        }
        return -1;
    }
};

34. 在排序数组中查找元素的第一个和最后一个位置

难度中等2035收藏分享切换为英文接收动态反馈

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

0 <= nums.length <= 105
-109 <= nums[i] <= 109
nums 是一个非递减数组
-109 <= target <= 109

二分查找

需要对二分的边界喝两种解法有深刻的理解。左闭右开和左闭右闭最后的l和r分别代表什么都要有比较清晰认识

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        vector<int>ans;
        int l=0,r=nums.size(),mid;
        while(l<r)
        {
            mid=l+r>>1;
            if(nums[mid]>=target)
            r=mid;
            else
            l=mid+1;
        }
        if(r==nums.size()||nums[r]!=target)
        return {-1,-1};
        ans.push_back(r);
        l=0,r=nums.size();
        while(l<r)
        {
            mid=l+r>>1;
            if(nums[mid]>target)
            r=mid;
            else
            l=mid+1;
        }
        ans.push_back(r-1);
        return ans;
    }
};

35. 搜索插入位置

难度简单

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为 无重复元素 的升序排列数组
-104 <= target <= 104

二分查找

二分查找标准题

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int l=0,r=nums.size(),mid;
        while(l<r)
        {
            mid=l+r>>1;
            if(nums[mid]==target)
            return mid;
            else if(nums[mid]>target)
            r=mid;
            else
            l=mid+1;
        }
        return r;
    }
};

de.cn/problems/search-insert-position/)

难度简单

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为 无重复元素 的升序排列数组
-104 <= target <= 104

二分查找

二分查找标准题

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int l=0,r=nums.size(),mid;
        while(l<r)
        {
            mid=l+r>>1;
            if(nums[mid]==target)
            return mid;
            else if(nums[mid]>target)
            r=mid;
            else
            l=mid+1;
        }
        return r;
    }
};