本系列文章主要对Bug类路径规划算法的原理进行介绍,在本系列的第一篇文章中按照时间顺序梳理了自1986年至2018年Bug类路径规划算法的发展,整理了13种BUG系列中的典型算法,从本系列的第二篇文章开始依次详细介绍了其中具有代表性的BUG1、BUG2、Tangent BUG、I-BUG、RandomBug、BugFlood等算法。
本篇文章作为本系列文章第四篇文章,主要对I-BUG 算法进行介绍
本系列其他文章见:BUG系列路径规划算法原理介绍——总结篇
一、I-BUG 算法的提出背景
前面介绍的bug算法可以访问他们访问的每个地方的确切坐标,并且在某些情况下可以访问他们行进的确切距离。那么机器人是否可以在不收集所有这些信息的情况下导航到目标。它可以在没有任何坐标的情况下达到目标吗?
基于以上动机Kamilah Taylor 和 Steven M. LaValle于2009年在论文《I-Bug: An intensity-based bug algorithm》中提出了I-Bug算法,其规划示例如下图所示。

论文链接:https://ieeexplore.ieee.org/abstract/document/5152728
论文DOI: 10.1109/ROBOT.2009.5152728
I-BUG算法使用了最少的感知信息,不需要机器人的定位信息,在很多无法定位、定位信息不准确的场景或者里程计累计误差较大的场景,存在较大的潜在应用价值,但是相应他是一种有源的算法,即需要在目标点处发出某种强度信号,来引导机器人前往目标点,使用I-BUG算法的机器人仅需要搭载三种传感器。
二、机器人搭载的传感器及其作用
(1) contact sensor:接触传感器
接触传感器用于判断机器人是否于障碍物接触。若机器人与障碍物接触则将变量ht(x)设为1,否则将其设为0,其中x表示机器人的当前位置。
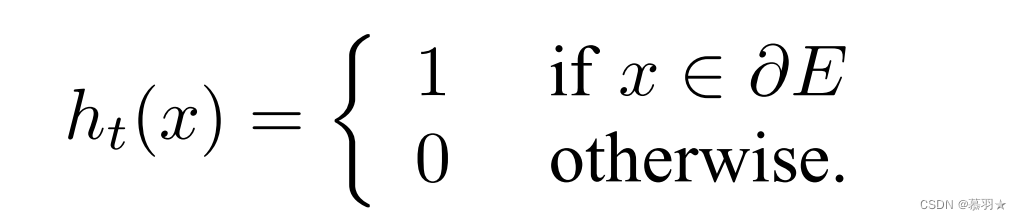
(2) intensity sensor:强度传感器
强度传感器用于指示来自位置p的信号的强度,在论文中,假设在目标点处存在一个Tower,可以理解为信号塔,会发出某种强度信号,如果这种强度信号是径向对称的,可以认为离信号塔越近的位置信号越强,强度传感器能够接收到目标点处的信号塔发出的这种强度信息,并能判断其强度大小,其数学表达式为:hi(x) = m(p − pt),其中p表示机器人当前位置,pt表示信号塔,也就是目标点所在位置,在径向对称强度信号中,m(p)可以简单的采用以下公式计算:
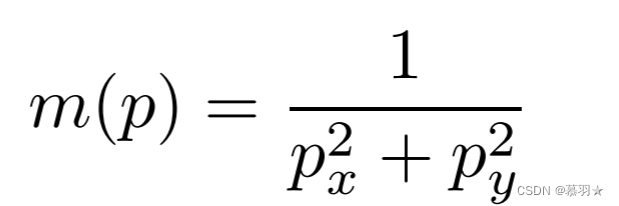
并将m(p)的值限定在0~1之间,并规定信号塔处m(pt)=1
(3) tower alignment sensor 或 gradient alignment sensor
在径向对称强度信号的场景中,第三种传感器采用塔架对准传感器或者梯度对准传感器都可以,而在非径向对称强度信号的场景,只能采用梯度对准传感器。
塔架对准传感器需要判断机器人前进的方向是否朝着信号塔,也就是目标点。 朝向信号塔时规定ha(x)=1,否则为0;前面介绍的BUG1、BUG2、Tangent BUG算法中机器人都存在朝着目标点方向直行的行为,I-BUG算法中依然存在该行为,所以需要采用塔架对准传感器来判断机器人的朝向。
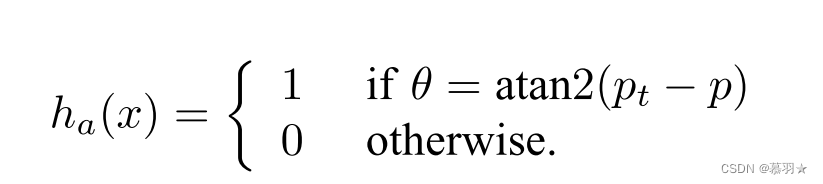
梯度对准传感器用于判断机器人是否面向m的最陡上升方向, 面向m的最陡上升方向时规定ha(x)=1,否则为0;在径向对称强度信号的环境中,面向m的最陡上升方向也就是对准塔架的方向,此时两种传感器的效果是相同的。
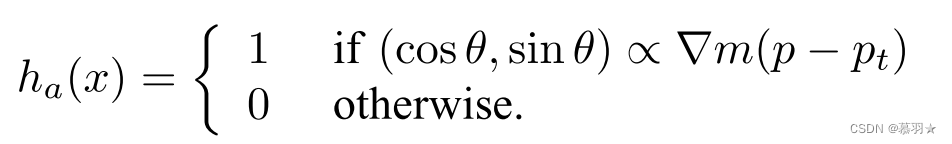
然而在非径向对称强度信号环境中,m(p)不再是上面表达式所示的那种简单的只与偏离信号塔的位置有关的模型,也就是说在偏离信号塔距离相同的位置中,其m(p)值可能不再相同,等m(p)值线不再是以信号塔为圆心的的一系列同心圆,而是不规则的封闭曲线,此时机器人就不能简单的朝着信号塔运动了,而是需要面向m的最陡上升方向运动,此时只能采用梯度对准传感器。
三、I-BUG算法的基础运动单元
I-BUG算法包含三种基础运动:u_fwd 、u_ori、u_fol
(1) u_fwd运动:u_fwd运动即机器人沿其面对的方向直行,仅在以下情况下之一发生时停止:
①接触障碍物 (ht(x) = 1)
② 撞击塔 (hi(x) = 1),即已经达到目标点
③ 检测到沿其运动线的局部强度最大值。
注:在径向强度对称信号的情况下,仅在①和②发生时退出,因为在径向强度对称信号的情况下,机器人执行u_fwd运动时m(p)是不断增大的,不会遇到局部强度最大值。
(2) u_ori运动:u_ori运动即机器人进行逆时针旋转,仅在与塔架对齐或与面向m的最陡上升方向时,即ha(x) = 1时停止。
(3) u_fol运动: u_fol运动即机器人逆时针绕障碍物边界移动,始终保持左侧接触障碍物,仅在强度m(p)达到局部最大值时才停止。
四、径向对称强度信号下的算法流程
机器人规划过程中需要存储两个强度值iL和iH,强度iH是通过完成u_fwd运动接触当前障碍物时观察到的强度。强度iL是在执行u_fwd运动之前获得的强度值。强度iL用于与当前强度hi(x) 进行比较,来确定u_fwd运动是否导致机器人发生移动。
径向对称强度信号下的算法流程步骤如下图所示:

机器人从起始点出发,执行步骤1,将此时的强度值记录到iL中。然后执行步骤2,机器人开始执行u_ori运动使得机器人朝向目标点所在的方向,然后执行u_fwd运动,机器人开始朝着目标点运动,直至满足u_fwd运动停止的条件之一,比如接触到障碍物,。
执行步骤3,判断当前的强度值hi(x)是否为1,若为1,则说明已达到目标点,退出规划。若不为1,继续执行步骤4,判断iL是否等于hi(x),即判断步骤2中执行u_fwd运动前后机器人所在位置的强度值有没有发生改变,借此来判断执行u_fwd运动是否使机器人进行移动,若iL不等于hi(x),说明机器人发生了移动,将当前的强度值储存在iH中来更新iH值。
执行步骤5,机器人开始执行u_fol行为,即机器人沿着障碍物边缘运动直至当前强度值到达局部最大值时停止,执行步骤6,判断当前强度的局部最大值是否大于开始绕行时的强度值iH,若不大于,则认为当前的强度局部最大值劣于开始绕行的位置,在径向强度对称的情况下,即认为机器人当前位置比开始绕行的位置更偏离目标点,则执行步骤7,并返回到步骤5继续绕行,直至到达下一个局部强度最大值处停止,然后再次执行步骤6,以此循环执行步骤5~7,直至当前的局部强度最大值大于开始绕行的强度值iH,返回步骤1,开始尝试离开当前障碍物。
假设机器人当前处于下图中的③处,其强度值大于开始绕行的②处,结束步骤5 ~ 7的循环,返回了步骤1,并依次完成步骤1 ~ 3,到步骤4时发现,iL=hi(x),即在步骤2中因为朝向目标点方向上接触障碍物导致u_fwd行为实际上没有能够让机器人移动,即机器人尝试离开当前障碍物失败,再次回到了步骤5继续绕行。寻找下一个局部强度最大值,且满足hi(x)> iH的点,再次尝试离开当前障碍物,若该点处朝向目标点处的方向不接触障碍物,则机器人有机会离开当前障碍物,如下图中的④处。
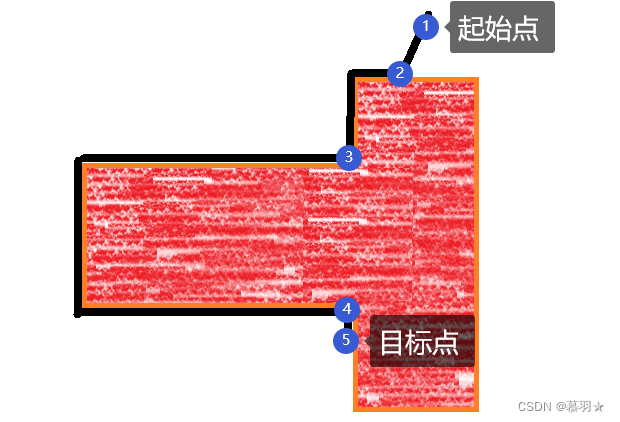
不断循环执行以上的1 ~ 7步,直至达到目标点,在步骤3处退出程序,结束规划。
论文中证明了,按照以上流程,机器人在有限的步骤之后到达目标点,而与特定环境E,E内部的初始机器人位置以及E中的目标点的位置无关。
注:以上结论成立的前提是起始点和目标点均位于环境中连通的可行区域E内!!!,如在下图所示的环境中,包含若干个独立的障碍物,还有一个在所有方向上无限向外延伸的外部障碍物,此时环境中连通的可通行区域即为图中的白色区域,即当起点和目标点均位于白色区域内以上结论才成立

五、非径向对称强度信号下的算法流程
非径向对称强度信号下的算法流程步骤如下图所示:

与径向对称强度信号下的算法流程相比的差异是插入了步骤5,有一点需要注意,论文中步骤1,写的将iL=ht(x),但是经过分析,这里很有可能是作者的笔误,应该还是跟径向对称强度信号下的算法流程中的步骤1一样,将iL=hi(x)。
那么非径向对称强度信号下,为什么要插入步骤5呢?在前面描述u_fwd行为的时候其退出条件有三种情况,但是在径向对称强度信号下,情况3不会发生,此时机器人停止u_fwd行为时要么是达到了目标点,要么是接触到了障碍物,也就是说排除达到目标点的特例,机器人停止u_fwd行为时是与障碍物接触的,这样接下来就可以进行绕行障碍物行为u_fol,然而在非径向对称强度信号下,u_fwd退出的时很有可能是因为满足情况3而退出,即检测到沿其运动线的局部强度最大值,此时机器人很有可能是不接触障碍物的,即无法进行后续的绕行行为u_fol,因此插入了步骤5,若此时接触传感器值为0,即不接触障碍物,将返回步骤1,并在步骤2中再次执行u_ori和u_fwd行为。以此循环步骤1~5,直至机器人达到目标点退出规划或接触障碍物,进行步骤6,开始u_fol行为。
也就是说,在非径向对称强度信号下,机器人可能需要朝不同的方向,执行多次直行行为,直至遇到障碍物才执行绕行行为,因为在非径向对称强度信号下,一次直行行为很有可能是不能接触到障碍物的。
下图显示了非对称强度场景下的示例路径
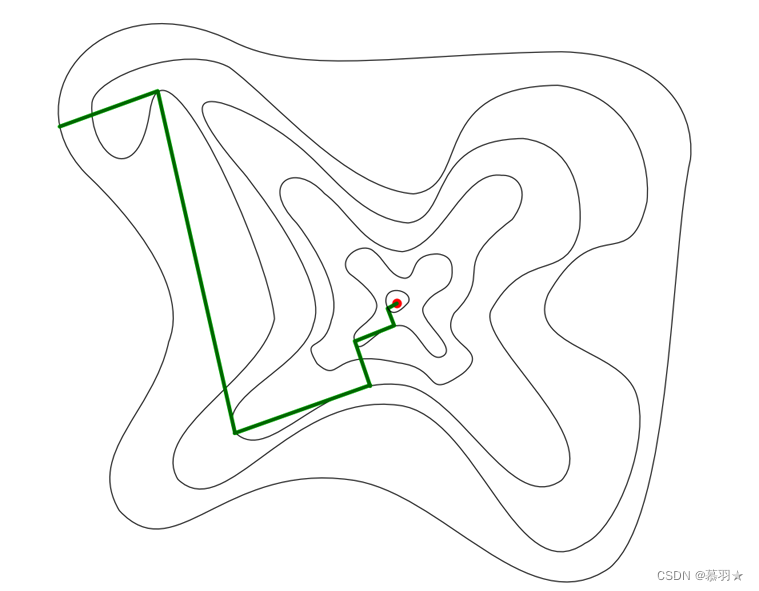
六、 I-BUG算法的缺陷
由于I-BUG算法使用了最少的感知信息,甚至抛弃掉了其自身的位置信息,也由此带来一个比较固有缺陷,I-BUG算法不能判断从起始点到目标点是否存在可行路径。
前面介绍的BUG1、BUG2、Tangent BUG算法其实都可以通过在绕行行为中若回到了开始绕行的位置依然没有找到可行的离开点来判断不存在从起始点到目标点的可行路径,然而I-BUG没有自身的位置信息,不能判断是否回到了开始绕行的地方,也就不能在有限的步骤之后判断出目标点无法到达。如在下面左图所示的情况中,目标点位于封闭的障碍物内部,机器人会不停的沿着障碍物的边缘一圈一圈的走,因为机器人不知道自己该不该停下来,若如下面右图所示的情况,则机器人绕行一段时间后便可到达目标点,但是由于自身位置的缺失,机器人不能很好的区分以下两种情况。除此之外,机器人不一定知道它是否多次返回同一障碍物。它可能在不知不觉中交替出现在几个障碍物之间。

其实以上的说法并不是绝对的,比如若是增加某种传感器,使机器人可以标记自己是否达到过某个地方,就像自然界中蚁群通过释放信息素的方式标记到过的地方,也是有可能判断出是否回到了开始绕行的地方,当然还要想办法排除掉干扰信息。
下图中给出了某种极端情况下的规划示例,在最终达到目标之前,机器人被反复发送到障碍物周围。
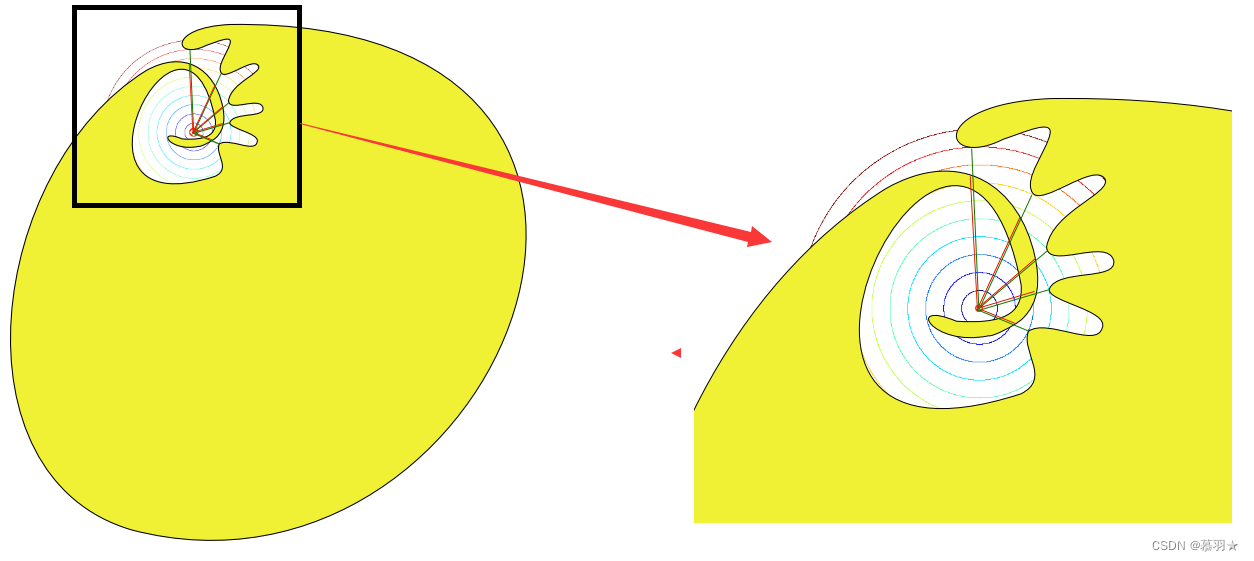
下图中给出了另外一种极端情况下的规划示例
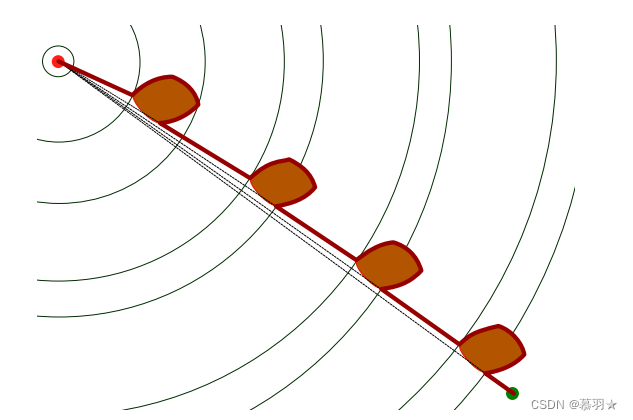
总的来说,I-BUG算法是一种有趣的尝试,大胆的抛弃了机器人的定位信息,也就不存在里程计累计误差这一说了,在某些场景下存在潜在的应用价值。




![[附源码]Python计算机毕业设计Django校园订餐系统](https://img-blog.csdnimg.cn/fb183291893647f988f0ab9c95bef7be.png)

![[附源码]Python计算机毕业设计Django校园运动会管理系统](https://img-blog.csdnimg.cn/3b9426cb92ee4597b741e30dcdd16e0c.png)


![[附源码]JAVA毕业设计砂石矿山管理系统(系统+LW)](https://img-blog.csdnimg.cn/b5c4c64c4e7a49fab7ca33bb905d49eb.png)