高中数学人教 A 版必修一 集合间的基本关系

学习目标：

(1)初步理解集合之间的包含与相等的含义;
(2)能识别给定集合的子集和真子案，了解空集含义:
(3)能进行自然语言、图形语言(Venn 图)、符号语言闻的转换，积萦抽象思维的经验，
提升数学抽象素养。

学习任务：

【学习任务一】掌握集合子集、相等、真子集的定义，辨析集合间的关系与上一节内容
的区别与联系，能使用适当的符号表示集合间的关系．
【学习任务二】掌握 Venn 图的含义，能进行自然语言、图形语言（Venn 图）、符号语
言间的转换，能使 Venn 图表示集合间的关系．

前题回顾：

用合适的方式描述的解集？

我们有两种方法来表示：

描述法：{}

列举法：{2,3}

那么，我们选择描述法和列举法的依据是什么呢？

描述法：结果太多，无法一一列举，我们采用共有的特征来表示它们。

列举法：选用列举法主要是因为我们能确定元素，并且可以将他们一一列出，所以可以非常直观的表示。

就这个题来说我们用列举法很直观，用描述法也行，但是建议能用描述法就用描述法，毕竟能显示这组数据的本源特征。

新课内容：

问题1:观察下面几个例子，类比实数之间的相等关系、大小关系，你能发现下面两个集合之间的关系吗?

(1) A={1,2,3}， B={1,2,3,4,5};

(2)C为立德中学高一(2)班全体女生组成的集合，D为这个班全体学生组成的集合；

(3) E={x.x是两条边相等的三角形}F={x]x是等腰三角形}。

观察上述几个例子，请同学们思考这几个问题:

1.你从哪个角度来分析每组两个集合间的关系?

2.请用集合的语言归纳概括上述三个具体例子的共同特点。

3.上述三组集合中，前两组的两个集合间的关系与第三组的两个集合间的关系有什么不同之处呢?

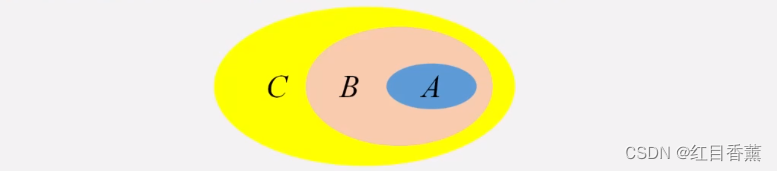
相信同学们不难发现:在(1)中，A={,2,3}, B={,2,3,4,5} ,集合A的任何一个元素都是集合B的元素.这时我们说集合A包含于集合B，或集合B包含集合A. (2)中C为立德中学高一(2)班全体女生组成的集，D为这个班全体学生组成的集合，集合C与集合D也有这种关。

一般地，对于两个集合A，B，如果集合A中任意一个元素都是集合B中的元素，就称集合A为集合B的子集(subset)，记作AB(或BA)，读作“A包含于B”(“或B包含A”) 。

符号解析：

包含符号：AB(或BA)，读作“A包含于B”(“或B包含A”) 。

Venn图

在数学中，我们经常用平面上封闭曲线的内部代表集合，这种图称为Venn图.这样，上述集合A与集合B的包含关系，可以用图1.2-1表示.
 

Venn图用于展示不同的集合之间的关系，也常常被用来帮助推导关于下一节集合运算的一些规律.它最大的优点就是直观，体现了数形结合思想，可以作为同学们学习集合这一章的辅助手段。

在(3)中，由于“两条边相等的三角形”是等腰三角形，因此，集合E，F都是由所有等腰三角形组成的集合.即集合E中任何一个元素都是集合下中的元素，同时，集合F中任何一个元素也都是集合E中的元素.这样，集合E的元素与集合F的元素是一样的。

一般地，如果集合A的任何一个元素都是集合B的元素，同时集合B的任何一个元素都是集合A的元素，那么集合A与集合B相等，

记作

A=B

也就是说，若AB，且BA，则A=B。

在定义了两个集合相等的关系后，请同学们再重新看一下开始的例子(1): AB,但4∈B，且4∉A。 我们把这样集合的关系作如下定义:

如果集合AB，但存在元素x∈B，且x∉A，就称集合A是集合B的真子集(proper subset)，记作
AB (或BA).

真子集的概念

我们再回顾一下刚刚的例子:

(1) A={1,2,3}， B={1,2,3,4.5} 

我们不难发现AB，但4∈B，且4∈A，所，以集合A是集合B的真子集。

通过刚刚真子集概念的学习，同学们不难发现集合包含的元素决定了集合间的关系。那请大家思考:如果一个集合不包含任何元素，我们怎么定义它呢?

例如，方程+1=0没有实数根，所以方程+1=0的实数根组成的集合就是这样一个集合，它不包含任何元素。

我们给出这样集合的定义:
一般地，我们把不含任何元素的集合叫做空集(empty set)， 记为∅，并规定:空集是任何集合的子集。

思考：

下面请大家思考一下: 0，{0}与∅三者之间有什么区别呢?它们之间又会有什么样的关系呢?

0∈{0};

0∉∅;

∅{0};

注意符号的使用。

问题2:同学们在学习了真子集和空集的概念之后，请思考以下几个问题:

1.子集和真子集的区别与联系是什么?
2.什么是空集?举几个空集的例子。

同学们类比实数关系，由上述集合之间的基本关系，不难得到下列结论:

(1) 任何一个集合是它本身的子集，即AA;
(2)对于集合A, B, C,如果AB，BC，那么AC。

例1：

写出集合{a,b}的所有子集，并指出哪些是它的真子集。

解:集合{a,b}的所有子集为0，{a)，{b}，{a,b}。真子集为0，{a}，{b}。

例2：

判断下列各题中集合A是否为集合B的子集，并说明理由:

(1) A={1,2,3},B={x|x是8的约数};
(2) A={x|x是长方形}

B={x|x是两条对角线相等的平行四边形} 。

例3：

用适当的符号填空:

(1) 0_{x| =x};
(2) -1{x| =x};
(3) 0_{x|=x}; 
(4) {0}_{x|=x};
(5) {0,1}_{x|=x)

答：

(1) {0}{x| =x};
(2) -1 ∉ {x| =x};
(3) ∅  {x|=x}; 
(4) {0}  {x|=x};
(5) {0,1}  {x|=x)

(1) 两个集合之间的基本关系有哪些?如何判断两个集合间的关系?

(2)你是如何研究集合间基本关系的?

(3)包含关系与属于关系有什么区别?比如：{a}A与a∈A?