线性搜索被定义为一种顺序搜索算法，它从一端开始，遍历列表的每个元素，直到找到所需的元素，否则搜索继续到数据集的末尾。

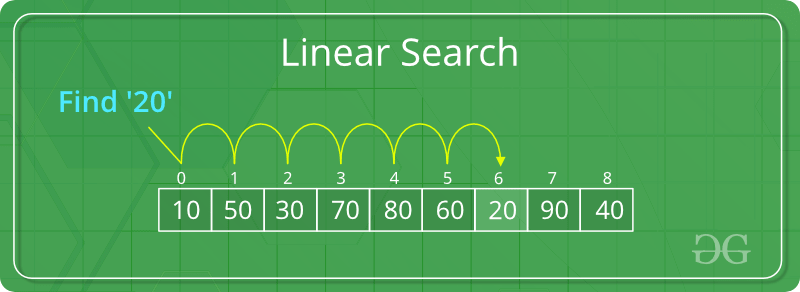
线性搜索算法是如何工作的？

在线性搜索算法中，

• 每个元素都被认为是键的潜在匹配项，并对其进行检查。
• 如果发现任何元素等于键，则搜索成功，并返回该元素的索引。
• 如果没有找到与该键相等的元素，则搜索结果为“未找到匹配项”。

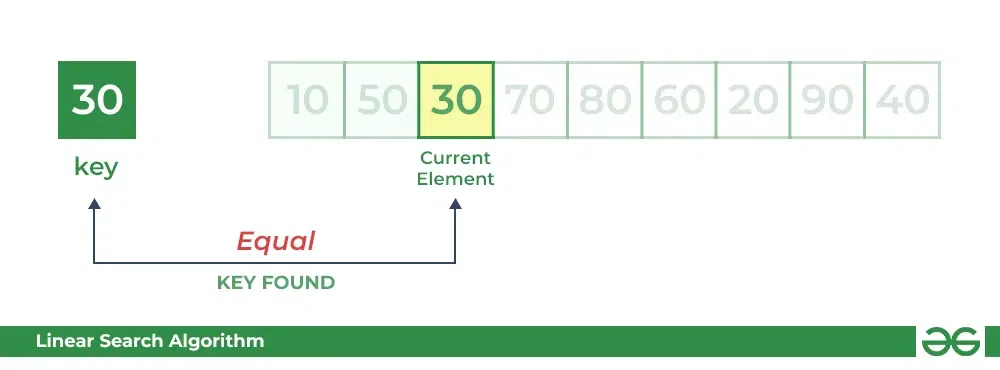
例如：考虑数组arr[] = {10，50，30，70，80，20，90，40}和key = 30

第1步：从第一个元素（index 0）开始，并将key与每个元素（arr[i]）进行比较。

1. 将key与第一个元素arr[0]进行比较。如果不相等，迭代器移动到下一个元素作为潜在匹配。
   
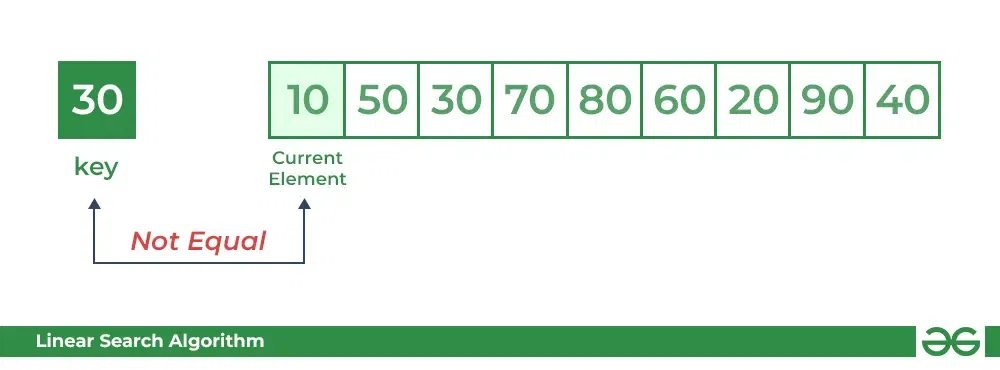
2. 比较key和下一个元素arr[1]。如果不相等，迭代器移动到下一个元素作为潜在匹配。
   
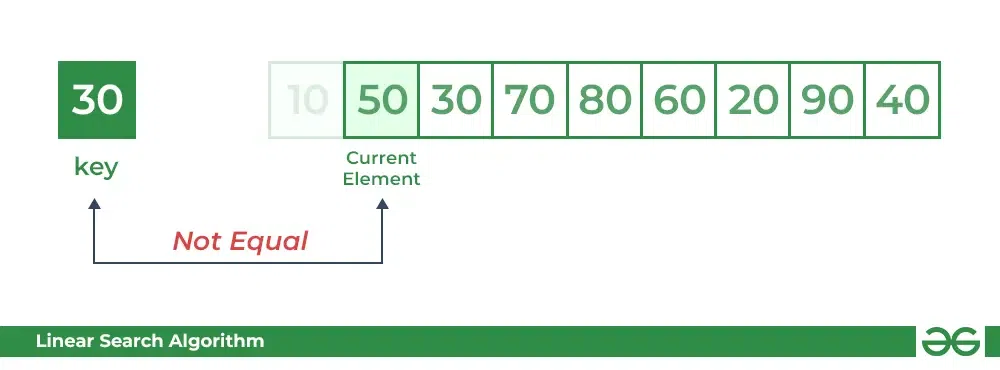
   第2步：现在当比较arr[2]和key时，值匹配。因此，线性搜索算法将产生一个成功的消息，并在找到键时返回元素的索引（这里为2）。
   

线性搜索算法的python实现

def search(arr, N, x):

    for i in range(0, N):
        if (arr[i] == x):
            return i
    return -1


# Driver Code
if __name__ == "__main__":
    arr = [2, 3, 4, 10, 40]
    x = 10
    N = len(arr)

    # Function call
    result = search(arr, N, x)
    if(result == -1):
        print("Element is not present in array")
    else:
        print("Element is present at index", result)

'''
Element is present at index 3
'''

线性搜索的复杂度分析

时间复杂度：

• 最佳情况：在最佳情况下，键可能存在于第一个索引中。所以最好的情况复杂度是O（1）
• 最坏情况：在最坏情况下，键可能存在于最后一个索引处，即，与列表中搜索开始的末端相对。所以最坏情况下的复杂度是O（N），其中N是列表的大小。
• 平均情况：O（N）

辅助空间：O（1）除了要遍历列表的变量外，没有使用其他变量。

线性搜索的优点

• 无论数组是否排序，都可以使用线性搜索。它可以用于任何数据类型的数组。
• 不需要任何额外的内存。
• 这是一个非常适合小数据集的算法。

线性搜索的缺点

• 线性搜索的时间复杂度为O（N），这反过来又使得它在大型数据集上很慢。
• 不适合大型阵列。

什么时候使用线性搜索？

• 当我们处理一个小数据集时。
• 搜索存储在连续内存中的数据集时。