Python电商数据分析系列-薪资预测
学习目标:
- 快速掌握简单且常用的数据分析任务
- 自己实现预测简单预测任务
学习内容:
- 搭建 Java 开发环境
- 掌握 Java 基本语法
- 掌握条件语句
- 掌握循环语句
学习对象
- 想快速入门的本科生
- 转行人员
- 想学习新技能,实现加薪的初级员工
学习要求:
- 掌握一门编程语言(最好用Pthon)
- 熟悉数据分析常用算法
- 对数据敏感、善于总结
内容介绍:
电商数据分析(电子商务数据分析):当用户在电子商务网站上有了购买行为之后,就从潜在客户变成了网站的价值客户。电子商务网站一般都会将用户的交易信息,包括购买时间、购买商品、购买数量、支付金额等信息保存在自己的数据库里面,所以对于这些客户我们可以基于网站的运营数据对他们的交易行为进行分析,以估计每位客户的价值,及针对每位客户的扩展营销的可能性。百度百科-电子商务数据分析
数据分析的重要性对于一个网站、公司的重要性是不言而喻的。各行各业都有着独立的数据存储中心,多有着专业的数据分析部门。通过分析行业数据、用户数据、公司数据,发现行业规律或行业状况、用户喜好、公司发展情况,针对其问题制定更加科学合理(符合实际)的规定、发展策略,以帮助自身拥有更好的发展前景。在电子商务领域,数据分析有着不可或缺的地位。
在当今这个经济、科技快速发展的时代,每秒都在产生海量数据信息。其中包括用户的喜爱度、点击率、退货率、员工忠诚度等信息非常重要。但如何从中获取到更有价值的信息,以及如果将这些信息转换为真正的盈利,才是最重要的!
对于一个电商公司,尤其对于高层管理人员、数据分析师来说,应该如何从产品信息、销售量、点击率、退货率、评价信息获取有价值的信息。

本系列内容主要任务有:用户行为分析、用户分类、预测未来用户的潜在需求、预测用户未来的消费行为。
本次内容:
预测未来的薪资
项目流程;
- 提出目标
- 获取数据
- 数据预处理
- 数据分析
- 分析结果并得出结论
- 验证结论
- 展示结果
本次内容使用的方法为:线性回归
在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。(这反过来又应当由多个相关的因变量预测的多元线性回归区别,而不是一个单一的标量变量。百度百科-线性回归
简单来说:因变量是被预测的变量(目标变量、输出),自变量是被用来进行预测的变量(使用此变量预测因变量、输入)。简单回归(简单线性回归)就是只有一个自变量和一个因变量的回归任务。而多元线性回归就是有多个自变量的回归任务。
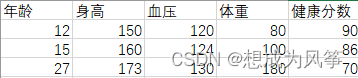
常被用于需求预测、销量预测、排名预测,或者用于控制某一个指标在一个范围内(预测的反问题)。例如:健康分数y与年龄、运身高、血压、体重的关系。(
y
=
a
∗
x
1
+
b
∗
x
2
+
c
∗
x
3
+
d
∗
x
4
y = a*x_1+b*x_2+c*x_3+d*x_4
y=a∗x1+b∗x2+c∗x3+d∗x4)。其中健康分数为因变量,其他为自变量。
如果用预测薪资呢?,如下数据:

线性回归模型:
一元线性回归方程(简单线性回归方程):
(
y
=
a
x
+
b
)
(y=ax+b)
(y=ax+b)
其中,a为斜率,b为截距。
多元线性回归方程:
(
y
=
a
1
∗
x
1
+
a
2
∗
x
2
+
a
3
+
x
3
+
.
.
.
+
a
n
∗
x
n
+
b
)
(y=a_1*x_1+a_2*x_2+a_3+x_3+...+a_n*x_n+b)
(y=a1∗x1+a2∗x2+a3+x3+...+an∗xn+b)
其中,
a
1
,
a
2
,
.
.
.
,
a
n
a_1,a_2,...,a_n
a1,a2,...,an为方程各自变量的系数,b为常数项。
使用Sklearn中的线性回归模型:
from sklearn.linear_model import LinearRegression
LinearRegression(fit_intercept=True,normalize=False,copy_x=True,n_jobs=1)
"""
参数含义:
1.fit_intercept:布尔值,指定是否需要计算线性回归中的截距,即b值。如果为False,那么不计算b值。
2.normalize:布尔值。如果为False,那么训练样本进行归一化处理。
3.copy_x: 布尔值。如果为True,会复制一份训练数据。
4.n_jobs:一个整数。任务并行时指定的CPU数量。如果取值为-1则使用所有可用的CPU。
属性:
1.coef_:权重向量
2.intercept_:截距b
方法:
1.fit(x,y):训练模型
2.predict(X):用训练好的模型进行预测,并返回预测值。
3.score(X,y):返回预测性能。计算公式为:score=(1-u/v)。其中u=((y_true-y_pred)**2).sum(),v=((y_ture-y_true.mean())**2).sum(),score最大值是1,但有可能是负值(预测效果很差)。score越大,预测性能越好。
"""
使用如下数据,完成薪资预测。(本次使用简单的数据,在文末会提供此份数据集以及更大的数据集。)
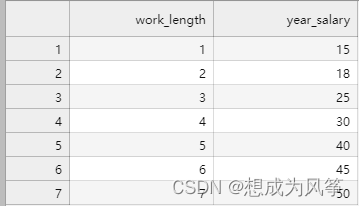
from sklearn import linear_model #导入sklearn机器学习库
import numpy as np #常用必要第三方库 数组
import pandas as pd #常用必要第三方库 数据处理
import matplotlib.pyplot as plt #常用必要第三方库 画图
#读取数据
data = pd.read_csv("D:\Python\python_code\电商数据分析系列CSDN\薪资预测\single_variable.csv") #注意修改为自己的路径,尽可能全部用英文路径.
print(data) #查看数据
print(data.shape) #查看数据维度
data.isnull().any() #查看数据是否在空数值
length = len(data['work_length']) #输入数据长度
X = np.array(data['work_length]).reshape([length,1]) #将数组转换成想要的形状,如何模型输入维度要求!
Y = np.array(data['year_salary'])
print(X.shape,Y.shape) #查看X,Y维度
#训练模型 train model
model = model.LinearRegression() #线性回归模型
model.fit(X,Y)
#训练完成后
print("斜率:{}".format(model.coef_)) #查看斜率
print("截距:{}".format(model.intercept_)) #查看截距
#根据斜率和截距可知回归方程: Y = 斜率 * X + 截距
#评价模型 score
print("score:{}".format(model.score(X,Y)))
#模型预测 prediction 加入预测第八年的薪资
x_salary = np.array(8).reshape(1,-1)
y_pred = model.predict(x_salary)
print("第八年的预测薪资:{}".format(y_pred))
如果使用包含有多种自变量的薪资数据呢?使用多元回归预测.参考如下案例:

从以上数据中,可知自变量有work_length education title city ,而因变量为 year_salary.
具体预测步骤如下:
#from sklearn import linear_model #导入sklearn机器学习库
import numpy as np #常用必要第三方库 数组
import pandas as pd #常用必要第三方库 数据处理
import matplotlib.pyplot as plt #常用必要第三方库 画图
#读取数据
mul_data = pd.read_csv("D:\Python\python_code\电商数据分析系列CSDN\薪资预测\many_variable.csv")
print(mul_data) #查看数据
print(mul_data.head()) #查看前五行数据 当然想看几行都可以.
print(mul_data.tail()) #查看后五行数据
mul_data.isnull().any() #查看数据是否存在空值.
"""
work_length False
education False
title False
city False
year_salary False
dtype: bool
"""
#数据预处理
"""
由于数据中存在有中文,在数据分析时,应该将其转换为可定量分析的数值数据.更好地提取数据特征.
"""
mul_data['education'] = mul_data['education'].replace(['本科','研究生'],[1,2])
mul_data['city'] = mul_data['city'].replace(['北京','上海','广州','杭州','深圳'],[1,2,3,4,5])
mul_data['title'] = mul_data['title'].replace(['P4','P5','P6','P7'],[1,2,3,4])
print(mul_data.head()) #查看处理后的前五行数据
#在多元回归任务中,有多个自变量. 导入模型前的数据封装.
X_mul = np.arrary(mul_data['work_length','education','title','city'])
Y_mul = np.array(mul_data['year_salary'])
print(X_mul.shape,Y_mul.shape)
#将数据集划分为训练集和测试集 train_test_split 函数 (可百度查询,后续也会提供链接)
x_train,x_test,y_train,y_test = train_test_split(X_mul,y_mul,test_size=0.3,random_state=0) #类似的数据切分方法也有还有很多,后续也会及详细介绍,尝试多种数据切分方法.
print(x_train.shape,y_train.shape) #查看训练集
print(x_test.shape,y_test.shape) #查看测试集
#训练模型 train_model
mul_model = linear_model.LinearRegression()
mul_model = mul_model.fit(x_train,y_train)
print(mul_model.coef_) #查看各个自变量的系数权重.
print(mul_model.intercept_) #查看方程的截距.
print(mul_model.score(x_train,y_train)) #查看模型得分
#模型预测
pred = mul_model.predic(x_test)
print(pred)
总结
第一次的内容主要为了初步了解电商数据分析的流程和一些常规的编程语句.后续内容将会持续增加新知识新内容. 一定要学会思考,学会迁移,学会举一反三(预测比赛成绩 \ 预测销售量 \ 预测产品寿命等等,是不是都可以.). 虽然本次案例是一个简单的回归预测分析,使用的是最简单的模型.在没有较高的预测精度要求时,可使用此方法.后续将会使用更加准确且复杂的模型.
数据集:链接:https://pan.baidu.com/s/1Eq3FJ5wgae7y3KTUG8F0pw
提取码:3ddf
–来自百度网盘超级会员V4的分享