题目要求
1.1. 任务要求
数据集：Facial Expression Recognition Challenge，共有7类：生气、恶心、害怕、快乐、悲伤、惊讶、中性。
基本要求（50%）：构建ResNet分类模型18层。
改进（30%）：增加两个ResNet模型结构（20/32/34/44/56/110/156）进行分类，分析分类结果及原因。
优化（20%）：基于分析的原因，自由选用新的卷积模型或者优化策略，提升分类精度。
1.2. 数据集介绍
Facial Expression Recognition Challenge (FER2013) 是一个用于面部表情识别的数据集。它包含了7个基本面部表情，即愤怒、厌恶、恐惧、快乐、中性、悲伤和惊喜。该数据集是由加州大学洛杉矶分校（UCLA）的研究人员和国际人脸识别比赛（FERET）提供的。FER2013数据集中包含了35887张图像，每张图像大小为48x48像素，分为三个部分：training、validation和testing。Training部分包含了28709张图像，validation部分包含了3589张图像，testing部分包含了3589张图像。每一个图像都被标记上了正确的面部表情类别。由于存在采集与标注错误，FER2013数据集上最高的人类识别精度也只有65%到70%。
FER2013数据集的特点与处理难点如下：
一、标签噪声。FER2013数据集的标签是通过众包（crowdsourcing）方式由人工标注的，存在一定的主观性和不一致性，有些图像的标签可能存在错误或模糊不清，这给模型的训练和评估带来了挑战。此外在FER2013数据集中存在着少量的失真乱码图像，这些图像可能会影响训练集的效果，但由于其数量较少，所以不会对整体效果造成太大的影响。
二、数据集的分布不均匀。FER2013数据集中每种面部表情的数据分布并不均匀。中性表情的数据量最多，而厌恶表情的数据量最少。这种不均匀的数据分布可能会影响训练要求数据平衡的模型，因此在训练过程中需要进行一些针对性的处理。
三、存在人脸朝向和角度问题。在FER2013数据集中，有些图像的人脸朝向或角度可能不是很理想，这可能会影响模型的训练效率和准确性。因此在使用这个数据集进行训练时，需要进行一些特殊的处理，如旋转或翻转图像。
任务分析
2.1. 数据预处理
2.1.1. 数据加载
FER2013数据集以csv 文件的形式保存，数据信息包含表情分类的标签、像素值、用途（训练、验证、测试），将数据按用途分为训练集、测试集和验证集三部分，其中训练集数据一共28708 条，训练集和验证集各3589条。将数据中的像素值还原为图像，可得到48 × 48的灰度图，共有7种表情：愤怒、厌恶、恐惧、高兴、悲伤、惊讶、中性。
2.1.2. 数据预处理
数据预处理包括了灰度化、裁剪、数据增强和标准化等步骤。
一、将输入的彩色图像转换为灰度图像，使用Grayscale()函数实现。
二、对灰度图像进行十次裁剪，并在裁剪的基础上进行水平或垂直镜像，得到十张图片。这个步骤使用TenCrop(size=40)函数实现，并通过Lambda函数将裁剪后的图片转换为张量，并将这些张量堆叠在一起。
三、在得到的张量上进行标准化，使用Normalize(mean, std)函数，将每个张量的每个元素减去均值并除以标准差。
如果进行数据增强（augment为True），则执行以下步骤：
（一）对原始图像进行随机裁剪，并将其缩放到指定的大小，使用RandomResizedCrop()函数实现。
（二）随机调整图像的亮度、对比度和饱和度，使用ColorJitter()函数实现。
（三）随机进行平移变换，即将图像沿水平和垂直方向随机平移一定比例的宽度和高度，使用RandomAffine()函数实现。
（四）随机进行水平翻转，使用RandomHorizontalFlip()函数实现。
（五）随机进行旋转变换，最多旋转10度，使用RandomRotation()函数实现。
（六）对图像进行五次裁剪，每次裁剪出尺寸为40的图片，并对这五张图片进行水平或垂直镜像获得十张图片，使用FiveCrop(40)函数实现。
（七）使用Normalize(mean, std)函数对张量进行标准化。
（八）在数据增强过程中随机擦除图像的一部分，以模拟图像中可能存在的遮挡或缺失，使用RandomErasing()函数实现。
（九）再次将处理后的张量进行堆叠，使用Lambda函数实现。
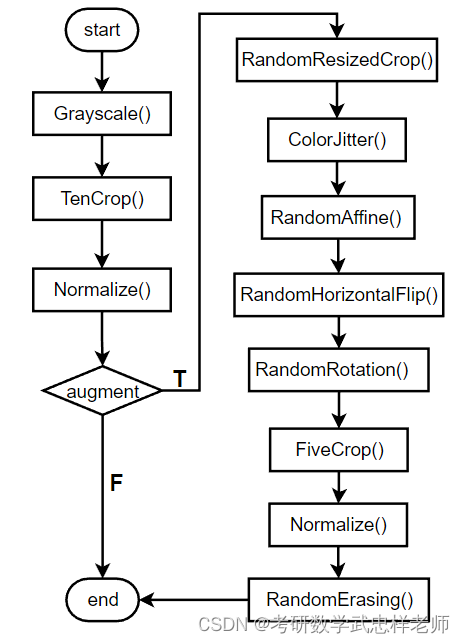
图2.1.2.1. 数据预处理流程图
2.2. 模型搭建
本次实验的模型搭建遵循深度学习模型的典型搭建流程：
一、输入数据：将原始数据输入到深度学习模型中进行处理和训练。
二、数据预处理：对输入数据进行一系列的预处理操作，例如图像数据的灰度化、裁剪、缩放或归一化等，以使数据适合于模型的输入要求。
三、模型定义：定义深度学习模型的结构，包括网络层、激活函数、连接方式等。模型的定义决定了模型的拓扑结构和参数。
四、初始化模型参数：在这个步骤中，对模型的参数进行初始化，通常使用随机初始化的方法。
五、定义损失函数：选择适当的损失函数来衡量模型输出与真实值之间的差异，常见的损失函数包括均方误差、交叉熵等。
六、定义优化器：选择合适的优化算法来更新模型的参数，例如随机梯度下降（SGD）、Adam等。
七、迭代训练模型：使用训练数据对模型进行迭代训练，通过反向传播和优化算法来更新模型参数，以逐渐优化模型性能。
八、前向传播计算输出：通过输入数据和训练好的模型，进行前向传播计算，得到模型的输出结果。
九、计算损失：使用定义的损失函数，计算模型输出结果与真实值之间的差异，得到损失值。
十、反向传播更新梯度：通过反向传播算法，计算损失函数对模型参数的梯度，用于更新模型参数。
十一、更新模型参数：使用定义的优化器，根据计算得到的梯度，更新模型的参数。
十二、重复训练迭代直至收敛：通过多次迭代训练，不断优化模型参数，使得模型在训练数据上的性能不断提升，直至模型收敛。
十三、模型评估：使用评估数据集对训练好的模型进行性能评估，计算指标如准确率、精确率、召回率等。
十四、使用模型进行预测：使用训练好的模型对新的未知数据进行预测，得到预测结果。
十五、输出预测结果：将模型预测的结果输出，可以是分类标签、概率值或其他形式的预测结果。
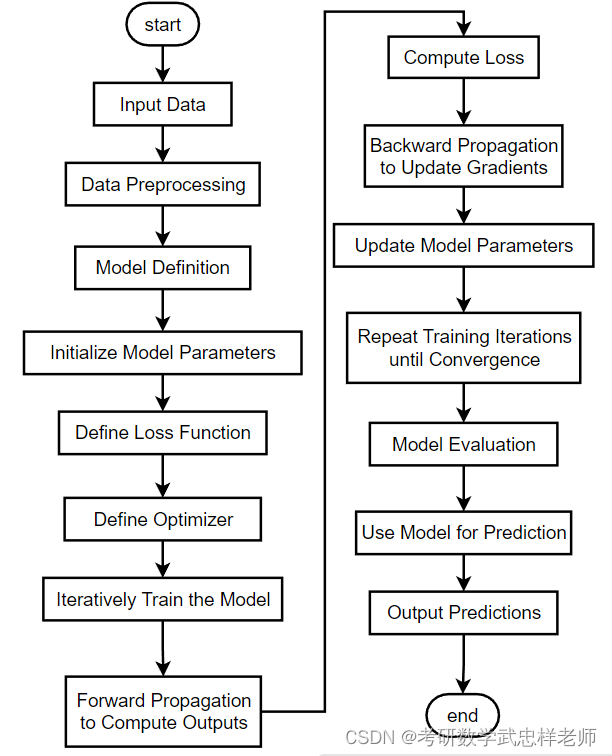
图2.2.1. 模型搭建流程图
2.3. 实验评价指标
2.3.1. 混淆矩阵
混淆矩阵（Confusion Matrix）又被称为错误矩阵，通过它可以直观地观察到算法的效果。它的每一列是样本的预测分类，每一行是样本的真实分类（反过来也可以），顾名思义，它反映了分类结果的混淆程度。
图2.3.1.1. 混淆矩阵
·P（Positive）：代表1，表示预测为正样本；
·N（Negative）：代表0，表示预测为负样本；
·T（True）：代表预测正确；
·F（False）：代表预测错误。
下列Positive和Negative表示模型对样本预测的结果是正样本（正例）还是负样本（负例）。True和False表示预测的结果和真实结果是否相同。
·True positives（TP）
预测为1，预测正确，即实际为1；
·False positives（FP）
预测为1，预测错误，即实际为0；
·False negatives（FN）
预测为0，预测错误，即实际为1；
·True negatives（TN）
预测为0，预测正确，即实际为0。
2.3.2. 准确率
准确率（Accuracy）衡量的是分类正确的比例。
模型原理
3.1. 深度神经网络的退化现象
ResNet是何凯明团队的作品，对应的论文Deep Residual Learning for Image Recognition斩获2016年CVPR 最佳论文。ResNet 的 Res 也是 Residual 的缩写，它的用意在于基于残差学习，让神经网络能够越来越深，准确率越来越高。
从以往的经验来看，网络的深度对模型的性能至关重要。当增加网络层数后，网络可以进行更加复杂的特征模式的提取，所以当模型更深时理论上可以取得更好的结果。但是更深的网络其性能一定会更好吗？实验发现深度网络出现了退化问题（Degradation problem）：网络深度增加时，网络准确度出现饱和，甚至出现下降。这个现象可以在下图中直观地看出来：56层的网络比20层网络效果还要差。这不是过拟合问题，因为56层网络的训练误差同样高。我们知道深层网络存在着梯度消失或者爆炸的问题，但是现在已经存在一些技术手段如批量归一化来缓解这个问题。因此，深度网络出现退化问题是非常令人疑惑的。
图3.1.1. CIFAR-10在20层和56层网络上的训练误差和测试误差
3.2. 残差结构
ResNet也称为残差网络，是由残差块（Residual Building Block）构建而成的。论文提出了两种映射：identity mapping（恒等映射），指的是右侧标有x的曲线；residual mapping（残差映射），残差指的是F(x)部分。最后的输出是F(x)+x。F(x)+x的实现可通过具有shortcut connections的前馈神经网络来实现。shortcut connections是跳过一层或多层的连接。图中的weight layer指卷积操作。如果网络已经达到最优，继续加深网络，residual mapping将变为0，只剩下identity mapping，这样理论上网络会一直处于最优状态，网络的性能也就不会随着深度增加而降低。残差块由多个级联的卷积层和一个shortcut connections组成，将二者的输出值累加后，通过ReLU激活层得到残差块的输出。多个残差块可以串联起来，从而实现更深的网络。
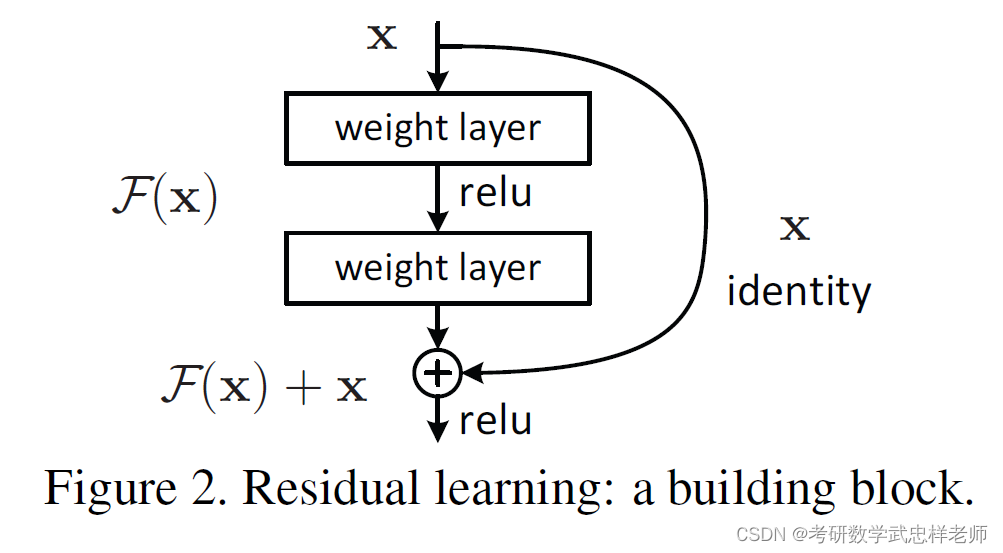
图3.2.1. 残差结构
残差块有两种设计方式。左图针对较浅的网络，如ResNet-18/34；右图针对较深的网络，如ResNet-50/101/152，使用此方式的目的就是为了降低参数数目。
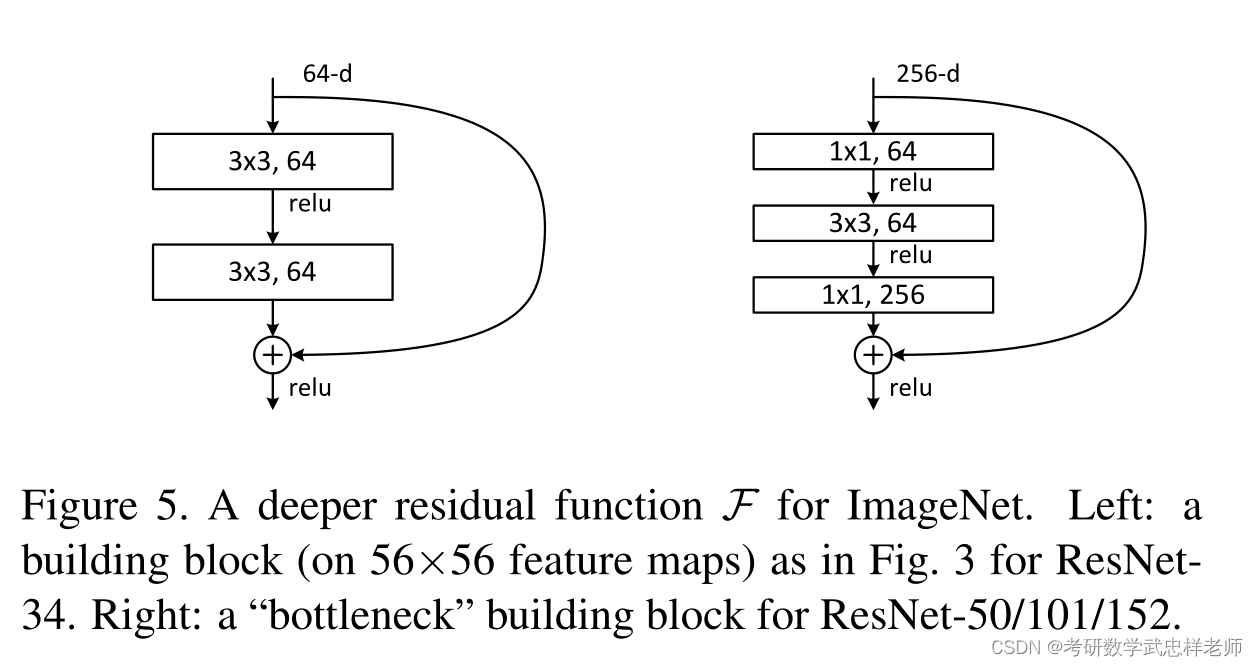
图3.2.2. 两种残差块的设计
论文中给出了5种不同层数的ResNet，ResNet-18/34是进行两层卷积的残差，ResNet-50/101/152是进行三层卷积的残差，分别对应于上图中的残差块的两种设计方式。ResNet-18/34对应的每个残差块的卷积kernel大小依次是3*3和3*3，ResNet-50/101/152对应的每个残差块的卷积kernel大小依次是1*1、3*3和1*1。以34层为例，1个卷积(conv1)+3残差块*2个卷积(conv2_x)+4个残差块*2个卷积(conv3_x)+6个残差块*2个卷积(conv4_x)+3个残差块*2个卷积(conv5_x)+最后的1个全连接层=34（这里的层仅指卷积层和全连接层）。
3.3. ResNet网络结构
ResNet的基本单元是残差块（Residual Block），如下图所示：
图3.3.1. 残差块的简明表示
残差块中包含两个卷积层和一个跨层连接。跨层连接将输入直接加到输出上，即y=F(x)+x，其中F(x)表示残差块中的卷积操作，x表示输入，y表示输出。
ResNet的整个网络结构如下图所示。ResNet由多个残差块组成，其中每个残差块包含多个卷积层和一个跨层连接。网络的最后一层是一个全连接层，用于输出分类结果。
图3.3.2. ResNet网络结构简明表示
ResNet的计算步骤如下：一、输入数据经过一个卷积层，得到特征图。二、特征图经过多个残差块，其中每个残差块包含两个卷积层和一个跨层连接。三、最后一个残差块的输出经过一个全局平均池化层，得到一个特征向量。四、特征向量经过一个全连接层，得到分类结果。
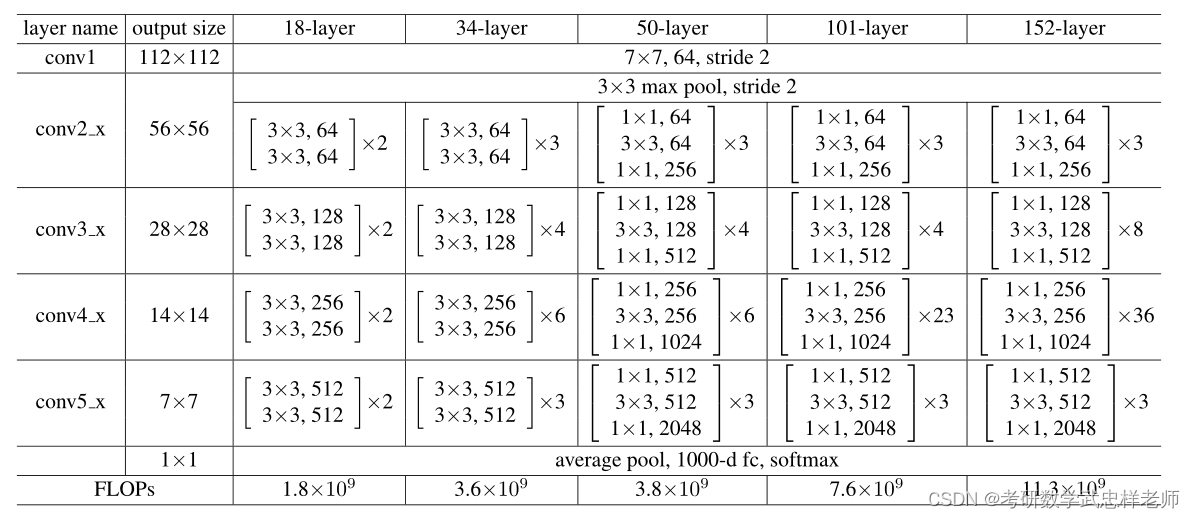
图3.3.3. ResNet网络结构
基础实验与分析
4.1. 实验环境
4.1.1. MindSpore简介
MindSpore是华为公司自研的最佳匹配昇腾AI处理器算力的全场景深度学习框架，为数据科学家和算法工程师提供设计友好、运行高效的开发体验，推动人工智能软硬件应用生态繁荣发展，目前MindSpore支持在EulerOS、Ubuntu、Windows系统上安装。本次实验在本地部署了MindSpore。
4.1.2. pytorch简介
PyTorch是由Meta AI（Facebook）人工智能研究小组开发的一种Python实现的深度学习库，专门针对 GPU 加速的深度神经网络（DNN）编程，目前被广泛应用于学术界和工业界。与TensorFlow的静态计算图不同，PyTorch的计算图是动态的，可以根据计算需要实时改变计算图。
PyTorch的优势如下。首先，PyTorch的设计追求最少的封装，尽量避免重复造轮子。PyTorch 的设计遵循tensor→variable(autograd)→nn.Module 三个由低到高的抽象层次，分别代表高维数组（张量）、自动求导（变量）和神经网络（层/模块），而且这三个抽象之间联系紧密，可以同时进行修改和操作。简洁的设计带来的另外一个好处就是代码易于理解：PyTorch的源码只有TensorFlow的十分之一左右，更少的抽象、更直观的设计使得PyTorch的源码十分易于阅读。其次，PyTorch 的灵活性不以速度为代价。在许多评测中，PyTorch 的速度表现胜过 TensorFlow和Keras 等框架。框架的运行速度和程序员的编码水平有极大关系，但同样的算法，使用PyTorch实现的那个更有可能快过用其他框架实现的。再次，PyTorch 是所有的框架中面向对象设计的最优雅的一个。PyTorch的面向对象的接口设计来源于Torch，而Torch的接口设计以灵活易用而著称，Keras作者最初就是受Torch的启发才开发了Keras。PyTorch继承了Torch的衣钵，尤其是API的设计和模块的接口都与Torch高度一致。PyTorch的设计最符合人们的思维，它让用户尽可能地专注于实现自己的想法，即所思即所得，不需要考虑太多关于框架本身的束缚。最后，PyTorch拥有活跃的社区：PyTorch 提供了完整的文档，循序渐进的指南，作者亲自维护论坛，供用户交流和求教问题。Facebook 人工智能研究院对 PyTorch 提供了强力支持，作为当今排名前三的深度学习研究机构，FAIR的支持足以确保PyTorch获得持续的开发更新。
4.2. 基本任务
4.2.1. ResNet-18模型结构
基本任务要求构建ResNet分类模型18层。ResNet-18网络结构如图所示：
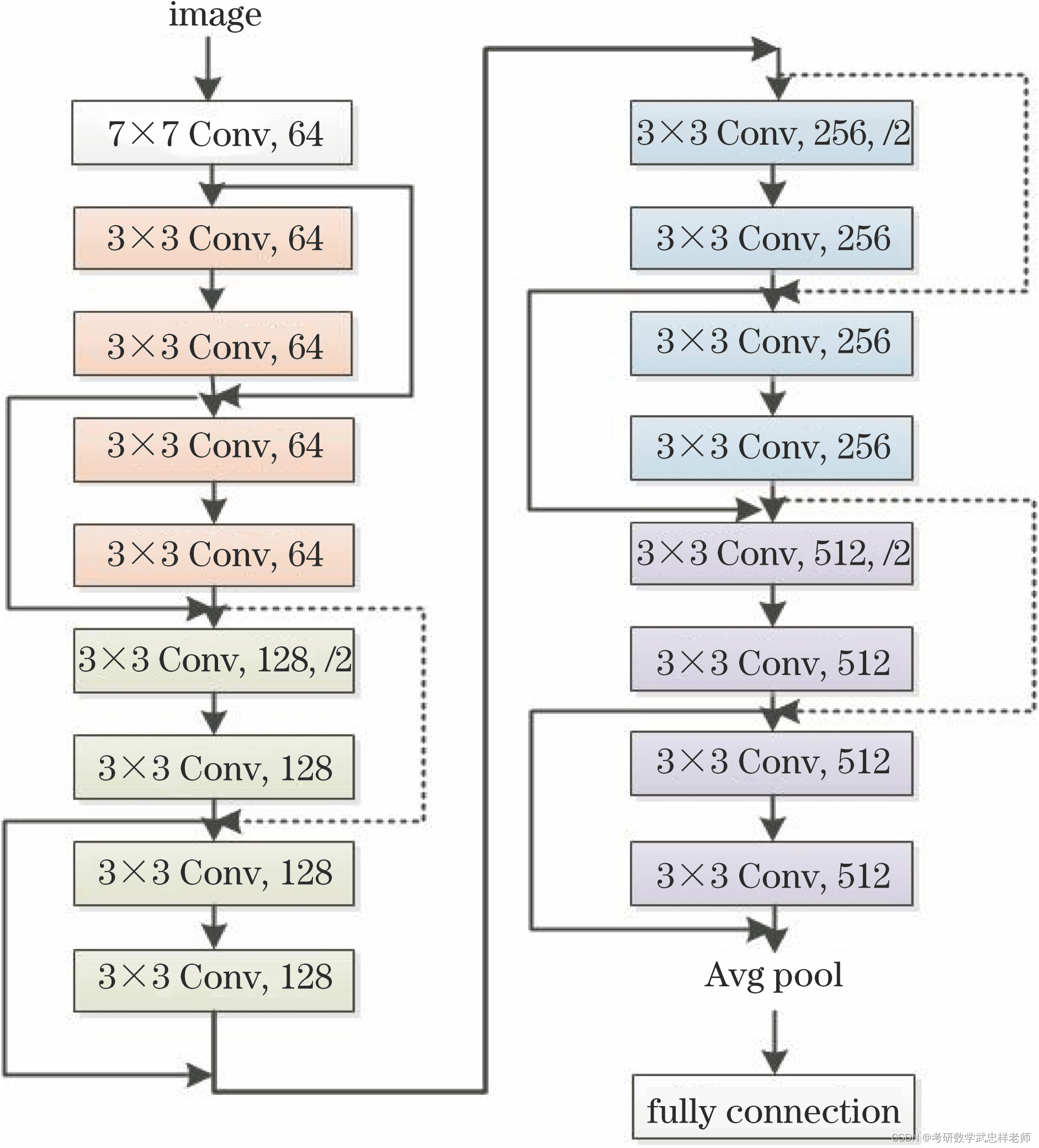
图4.2.1.1. ResNet-18网络结构图
结合具体代码分析，ResNet-18中，conv1是一个卷积层，输入通道为1，输出通道为64，卷积核大小为3x3，步长为1，填充为1。bn1是一个批量归一化层，用于对conv1的输出进行批归一化操作。
layer1是第一个残差层，调用了_make_layer方法来创建，输入通道为64，输出通道为64，包含2个BasicBlock残差块，步长为1。
layer2是第二个残差层，输入通道为64，输出通道为128，包含2个BasicBlock残差块，步长为2。
layer3是第三个残差层，输入通道为128，输出通道为256，包含2个BasicBlock残差块，步长为2。
layer4是第四个残差层，输入通道为256，输出通道为512，包含2个BasicBlock残差块，步长为2。
linear是一个全连接层，输入大小为512乘以BasicBlock的扩展因子，输出大小为num_classes，用于进行分类。
在前向传播方法forward中，输入数据通过conv1、bn1和ReLU激活函数后，依次经过layer1、layer2、layer3和layer4，即4个残差层。然后，对输出进行平均池化，将特征图的每个通道进行平均。接下来，通过形状变换将平均池化后的特征图展平为一维向量。最后，通过全连接层linear进行分类，输出预测结果。
总而言之，ResNet-18模型由一个卷积层、4个残差层和一个全连接层组成。每个残差层由2个BasicBlock残差块组成，其中每个BasicBlock包含两个卷积层和一个跳跃连接。这种结构可以有效地解决深度网络中的梯度消失和过拟合问题，使得网络能够更好地学习和表示复杂的特征。
4.3. 改进任务
改进任务要求增加两个ResNet模型结构进行分类并分析分类结果及原因。我构建了ResNet-20、ResNet-34和ResNet-50进行训练。
4.3.1. ResNet-20模型结构
ResNet-20模型由一个卷积层（Conv1）、一个批归一化层（BN1）、一个ReLU激活函数（ReLU1）、三个残差块（Layer1, Layer2, Layer3）、一个自适应平均池化层（AvgPool）和一个全连接层（FC）组成。不同的残差块在通道数和步长上有所区别，通过重复堆叠这些残差块，最终实现对输入图像的特征提取和分类。下面是ResNet-20的详细结构：
输入（Input）：图像数据
1、Convolutional Layer (Conv1):
输入通道数：num_channels
输出通道数：16
卷积核大小：3x3
步长（stride）：1
填充（padding）：1
2、Batch Normalization (BN1):
对Conv1的输出进行批归一化
3、ReLU Activation (ReLU1):
对BN1的输出进行ReLU激活函数操作
4、Residual Blocks (Layer1):
重复3个ResNetBlock
每个ResNetBlock包含两个3x3卷积层，输出通道数为16
残差块的输入通道数和输出通道数都为16
残差块之间的步长（stride）都为1
5、Residual Blocks (Layer2):
重复3个ResNetBlock
每个ResNetBlock包含两个3x3卷积层，输出通道数为32
残差块的输入通道数为16，输出通道数为32
第一个残差块的步长（stride）为2，其余残差块的步长都为1
6、Residual Blocks (Layer3):
重复3个ResNetBlock
每个ResNetBlock包含两个3x3卷积层，输出通道数为64
残差块的输入通道数为32，输出通道数为64
第一个残差块的步长（stride）为2，其余残差块的步长都为1
7、Adaptive Average Pooling (AvgPool):
自适应平均池化层，将最后一个卷积阶段特征图转换为大小为1x1的特征图
8、Fully Connected Layer (FC):
输入维度：64
输出维度：num_classes
输出（Output）：分类结果
4.3.2. ResNet-34模型结构
ResNet-18和ResNet-34都是基于BasicBlock，结构非常相似，差别只在于每个layer的block数，ResNet-18为[2，2，2，2]，ResNet-34为[3，4，6，3]。下面是ResNet-34的结构图：
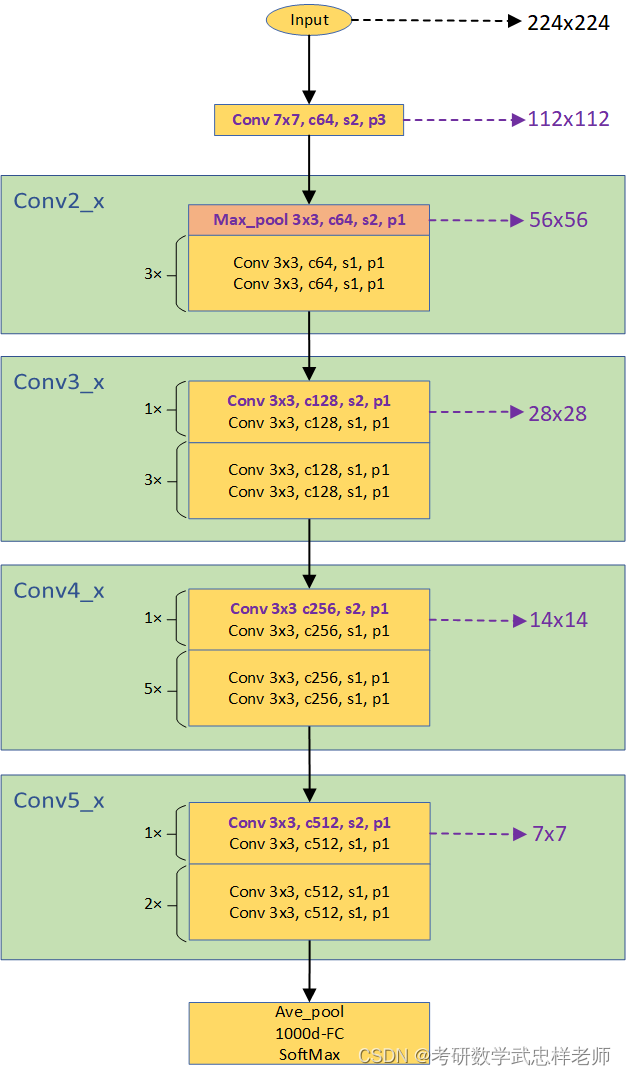
图4.3.2.1. ResNet-34网络结构图
4.3.3. ResNet-50模型结构
ResNet-50与ResNet-18/34的不同之处在于其残差结构使用BottleNeck而不是BasicBlock。ResNet中的BasicBlock和Bottleneck是两种不同类型的残差块，它们在网络结构和参数数量上存在一些区别。BasicBlock是ResNet中较简单的残差块，它由两个3x3的卷积层组成，每个卷积层后面跟着一个批标准化层和ReLU激活函数，通常用于ResNet-18和ResNet-34这样的浅层网络结构。
Bottleneck是ResNet中更复杂的残差块，主要用于处理较深的网络结构。Bottleneck由三个不同大小的卷积层组成：1x1卷积层、3x3卷积层和1x1卷积层。第一个1x1卷积层用于降低输入通道数，第二个3x3卷积层是主要的特征提取层，第三个1x1卷积层则用于恢复通道数。Bottleneck的设计旨在减少参数数量和计算复杂度，并提高网络的表达能力。
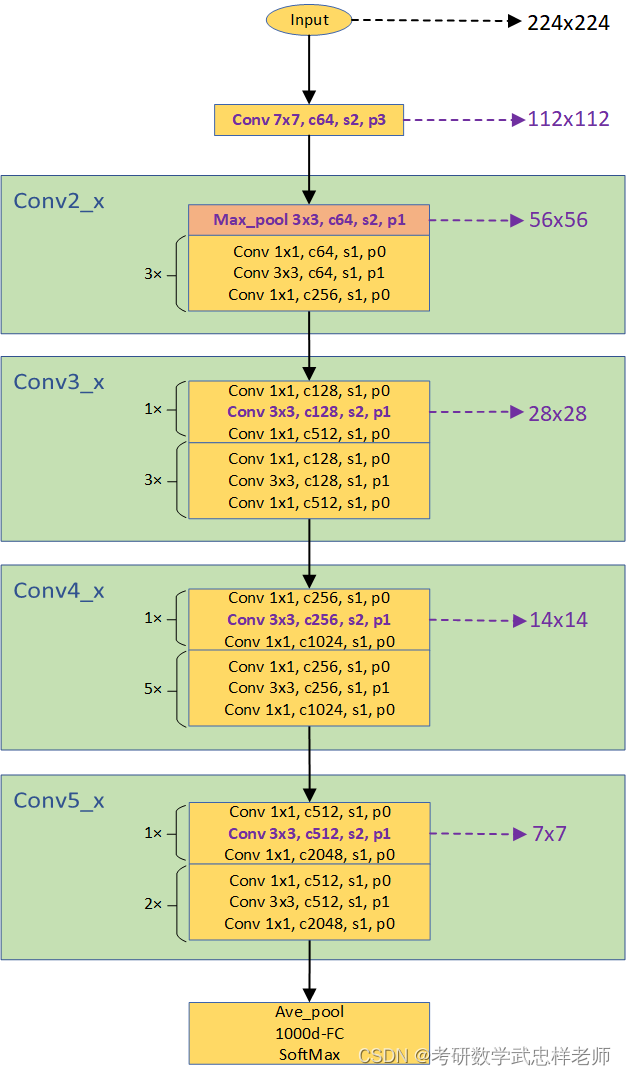
图4.3.3.1. ResNet-50网络结构图
4.4. 实验结果
将ResNet各版本模型分别训练200个epoch，结果如下。
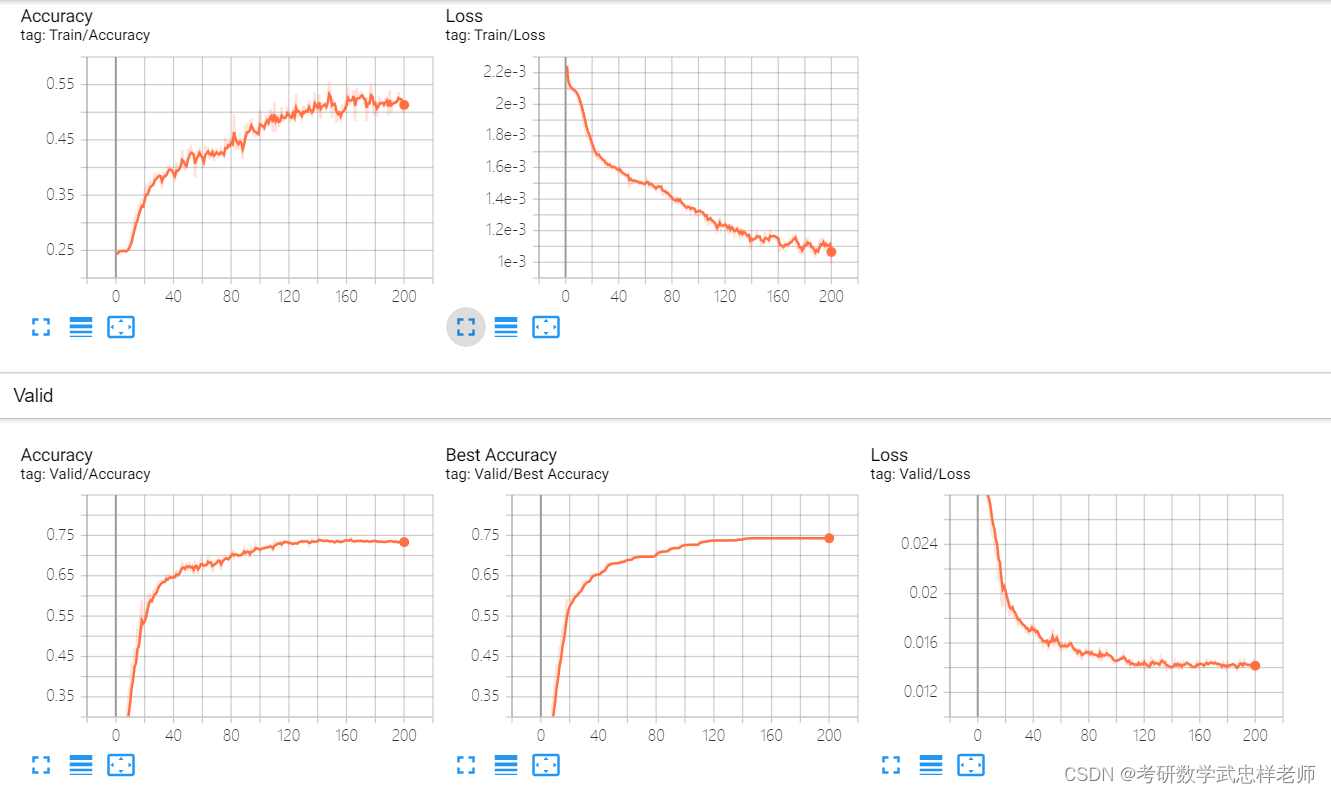
图4.4.1. ResNet-18结果可视化
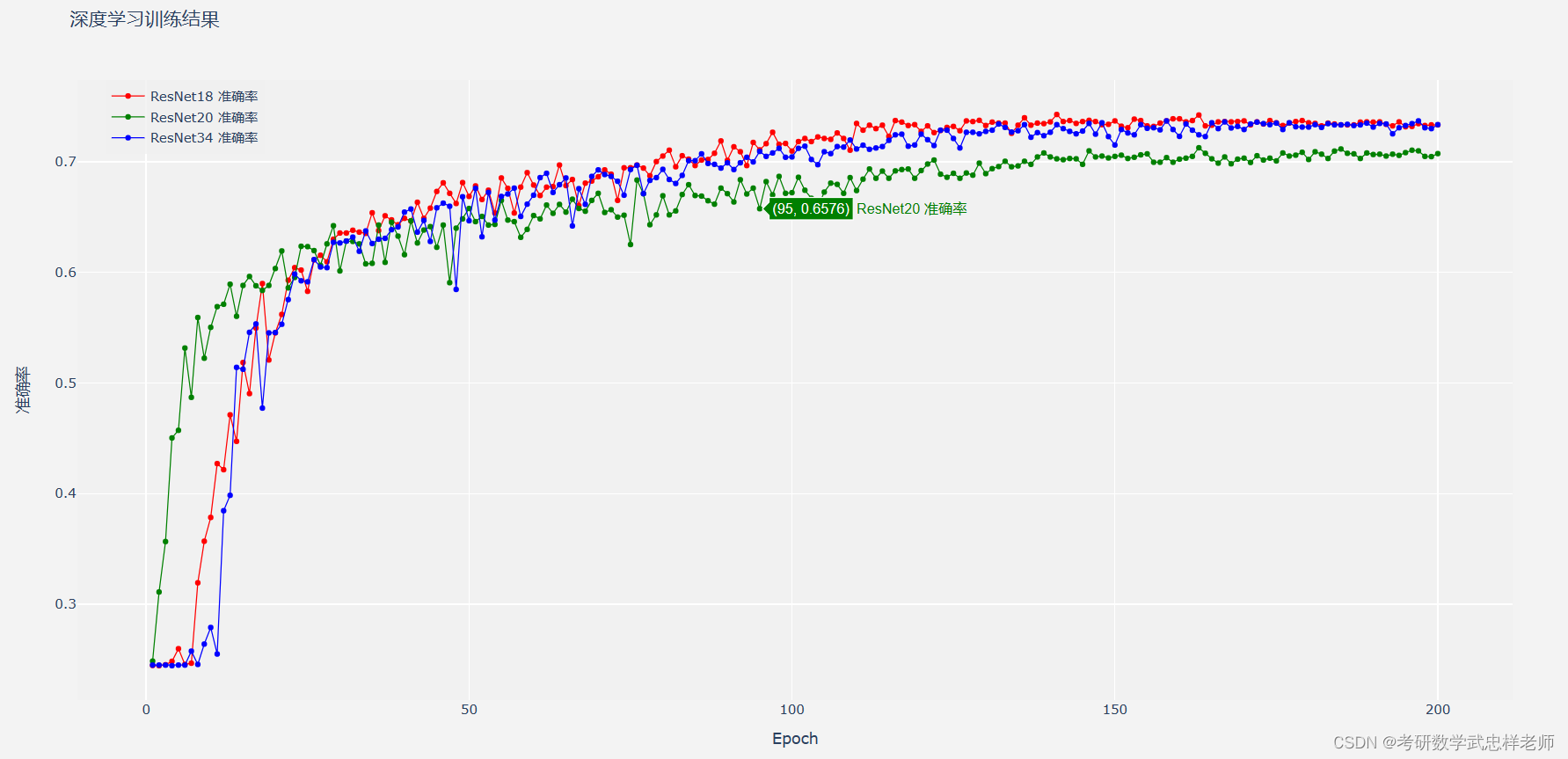
图4.4.2. ResNet-18/20/34准确率对比
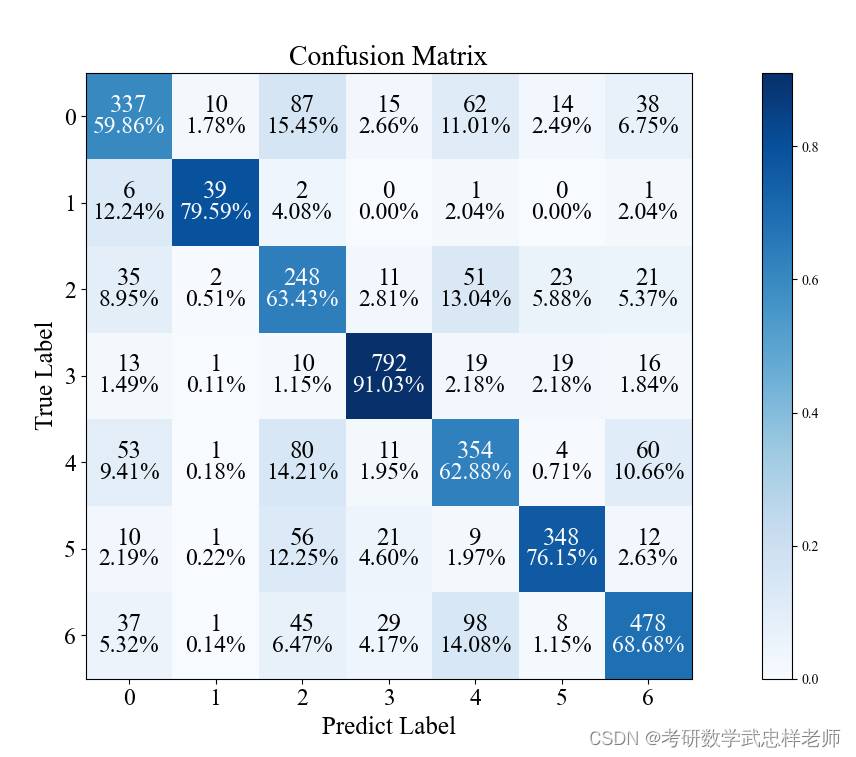图4.4.3. ResNet-18混淆矩阵
4.5. 结果分析
从准确率上看，ResNet-18和ResNet-34的性能较为相似，均优于ResNet-20，准确率最高能达到73%以上，这也超过了人类识别的准确率，效果较好。从分类结果上看，0（愤怒）和4（悲伤）两类的分类准确率较低，可能是因为这两种表情较为相似，难以区分。
根据ResNet的原理，随着层数的增加，模型性能至少不会下降，但在本次实验中，ResNet-18的性能反倒要比更深层的ResNet-20更好。分析其原因，可能有以下几个方面：一、数据集大小。如果训练数据集的规模相对较小，例如在小规模数据集上训练，更深的网络可能会导致过拟合。较浅的ResNet-18由于参数数量较少，更容易适应较小的数据集。二、网络复杂性。ResNet-20相比ResNet-18具有更多的层和更多的参数，这也增加了网络的复杂性和容量。在某些任务或数据集上，更深的网络可能会出现过拟合现象，而较浅的网络具有更好的泛化性能。
因此，在选择网络结构时，需要综合考虑网络的复杂性、数据集规模、训练资源和任务要求等因素，更深层的网络未必比较浅层的网络性能好。
模型优化
5.1. 选用其它模型
5.1.1. DenseNet
DenseNet于2017年在论文《Densely Connected Convolutional Networks》中被提出。DenseNet是一种深度学习网络架构，通过密集连接（Dense Connection）的设计使得每个层都能直接访问前面所有层的特征图。这种设计使得DenseNet具有更高的参数和计算效率，能够更好地传递信息和梯度，从而提升了网络的性能。DenseNet的主要组成部分是DenseBlock和Transition Layer。
DenseBlock是DenseNet的核心模块，由多个密集连接的层组成。每个层的输出都直接作为后面所有层的输入。具体而言，对于第l个层，它的输入包括前面l-1个层的输出，即 [x0，x1，x2，...，xl-1]，其中xi表示第i层的输出。那么第l个层的输出就是 [x0，x1，x2， ...，xl-1， xl]。这种密集连接的设计使得网络能够更好地利用先前层的特征，并且有助于更好地传递梯度和信息。在每个层内部，通常包含以下几个操作：Batch Normalization（批归一化）：用于规范化每个层的输入，加速网络的训练过程；ReLU激活函数：引入非线性，增加网络的表达能力；卷积层：通过卷积操作提取特征。DenseBlock的输出是每个层输出的连接，即特征图的维度会随着层数的增加而增加，这种密集连接的设计使得DenseNet能够更好地捕捉不同层次的特征。
Transition Layer用于控制特征图的尺寸和通道数，以降低网络的复杂度。它由一个1x1卷积层和一个2x2的平均池化层组成。1x1卷积层用于减少特征图的通道数，从而减少计算量。2x2的平均池化层用于减小特征图的尺寸，提取更全局的特征。通过Transition Layer，DenseNet能够在不同层次之间平衡计算量和特征的多样性。
在整个DenseNet中，DenseBlock和Transition Layer交替出现，形成多个DenseBlock组成的网络结构。最后通过全局平均池化层将特征图转换为向量，并通过全连接层进行分类。
DenseNet的优点包括：一、更高的参数和计算效率：由于每个层只需要输出自己的特征图，减少了参数的数量和计算的复杂性。二、更好的特征重用和信息流动：密集连接使得每个层都能直接访问前面所有层的特征图，有助于更好地传递信息和梯度。三、缓解梯度消失：密集连接使得梯度能够更好地传递，有助于更好地训练深层网络。
DenseNet可以视为ResNet的改进之一。ResNet中的主要思想是通过跳跃连接（即恒等映射）来解决梯度消失和信息传递的问题。每个ResNet块的输出是前面所有层的输入的简单相加。虽然这种设计有效地促进了梯度的流动，但也引入了大量的参数和计算成本。而DenseNet则通过密集连接的方式来改进ResNet，每个层都与前面所有层直接相连，并且每个层的输出都作为后面所有层的输入。这种密集连接的设计使得网络中的每个层都能够直接访问来自前面层的特征图，并将其自身的特征图传递给后面的层。这种设计带来了以下几个优势：
一、参数和计算效率：相比于ResNet的跳跃连接，DenseNet的密集连接减少了参数的数量，此外由于每个层可以直接访问前面层的特征图，它们不需要学习恒等映射，进一步减少了参数的数量和计算的复杂性。
二、特征重用和信息流动：由于每个层都能够直接访问前面所有层的特征图，DenseNet能够更好地重用先前层的特征，并且有助于更好地传递梯度和信息。这种密集连接的设计使得网络更加深厚，并且可以更好地捕捉不同层次的特征。
三、缓解梯度消失：每个层都可以通过直接访问前面层的梯度来传递梯度信息，这有助于更好地训练深层网络，避免梯度在传播过程中逐渐消失或爆炸。
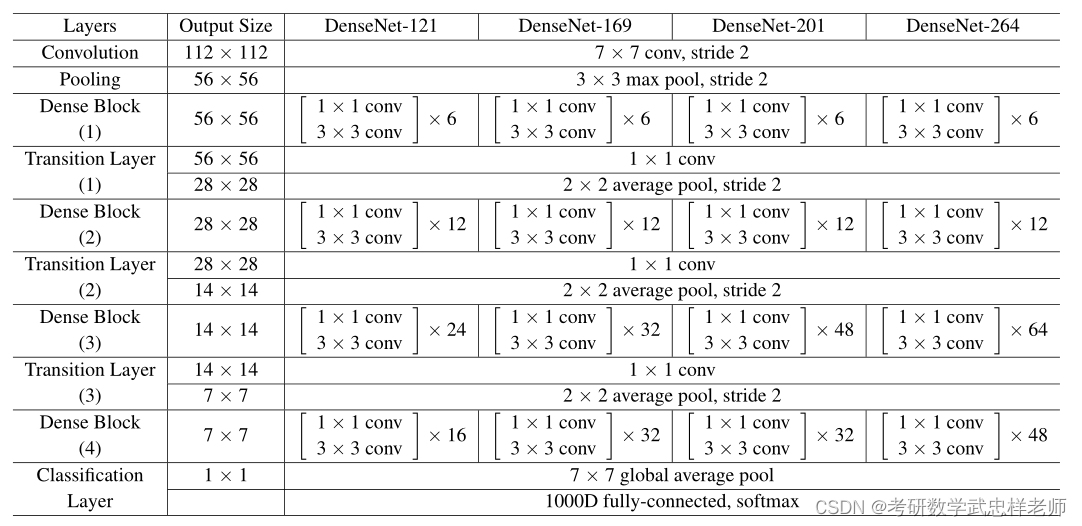
图5.1.1.1. DenseNet不同架构
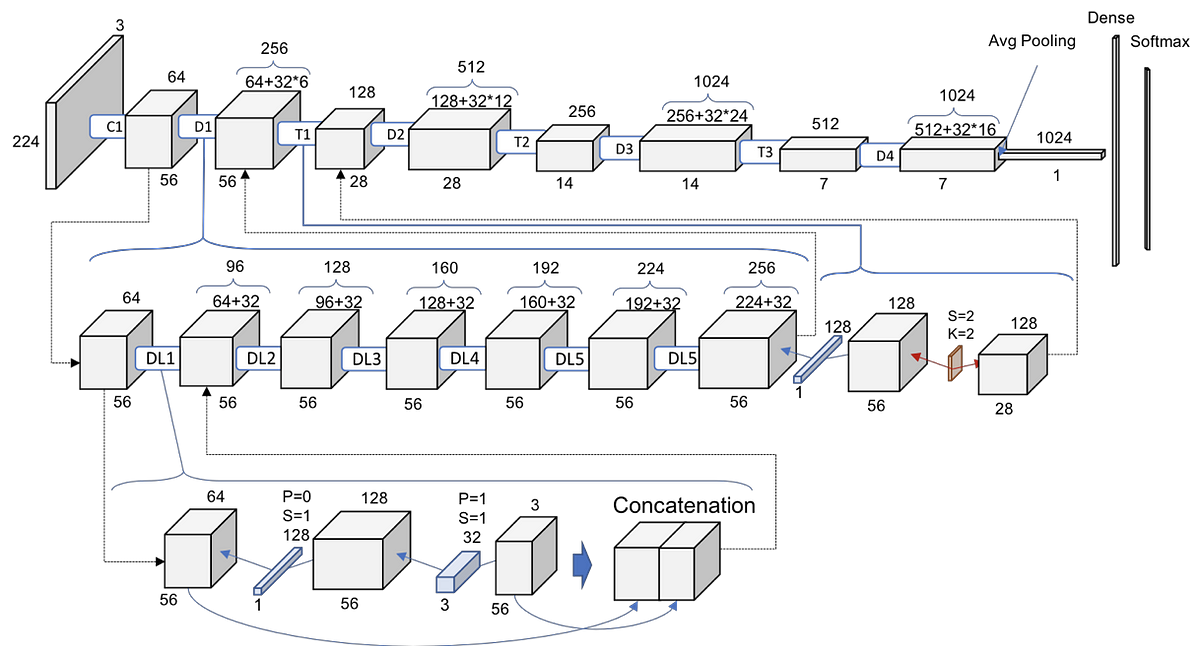
图5.1.1.2. DenseNet-121网络结构图
5.1.2. VGG
VGG网络的提出时间早于ResNet，可以说是在残差网络横扫天下之前的落日余晖。本次实验使用VGG的主要目的是与ResNet和DenseNet进行对比，以衬托后者的强悍性能。
VGG是由牛津大学的Visual Geometry Group提出的。VGG16相比AlexNet的一个改进是采用连续的几个3x3的卷积核代替AlexNet中的较大卷积核（11x11，7x7，5x5）。对于给定的感受野（与输出有关的输入图片的局部大小），采用堆积的小卷积核是优于采用大的卷积核，因为多层非线性层可以增加网络深度来保证学习更复杂的模式，而且代价还比较小（参数更少）。简单来说，在VGG中，使用了3个3x3卷积核来代替7x7卷积核，使用了2个3x3卷积核来代替5x5卷积核，这样做的主要目的是在保证具有相同感知野的条件下，提升了网络的深度，在一定程度上提升了神经网络的效果。
我们可以把VGG网络看成是数个vgg_block的堆叠，每个vgg_block由几个卷积层+ReLU层，最后加上一层池化层组成。VGG网络名称后面的数字表示整个网络中包含参数层的数量（卷积层或全连接层，不含池化层）。以VGG19为例，5个VGG块的卷积层数量分别为（2，2，4，4，4），再加上3个全连接层，总的参数层数量为19，因此命名为VGG19。VGG-11的5个VGG块的卷积层数量分别为（1，1，2，2，2），再加上3个全连接层；VGG-13的5个VGG块的卷积层数量分别为（2，2，2，2，2），再加上3个全连接层；VGG-16的5个VGG块的卷积层数量分别为（2，2，3，3，3），再加上3个全连接层。
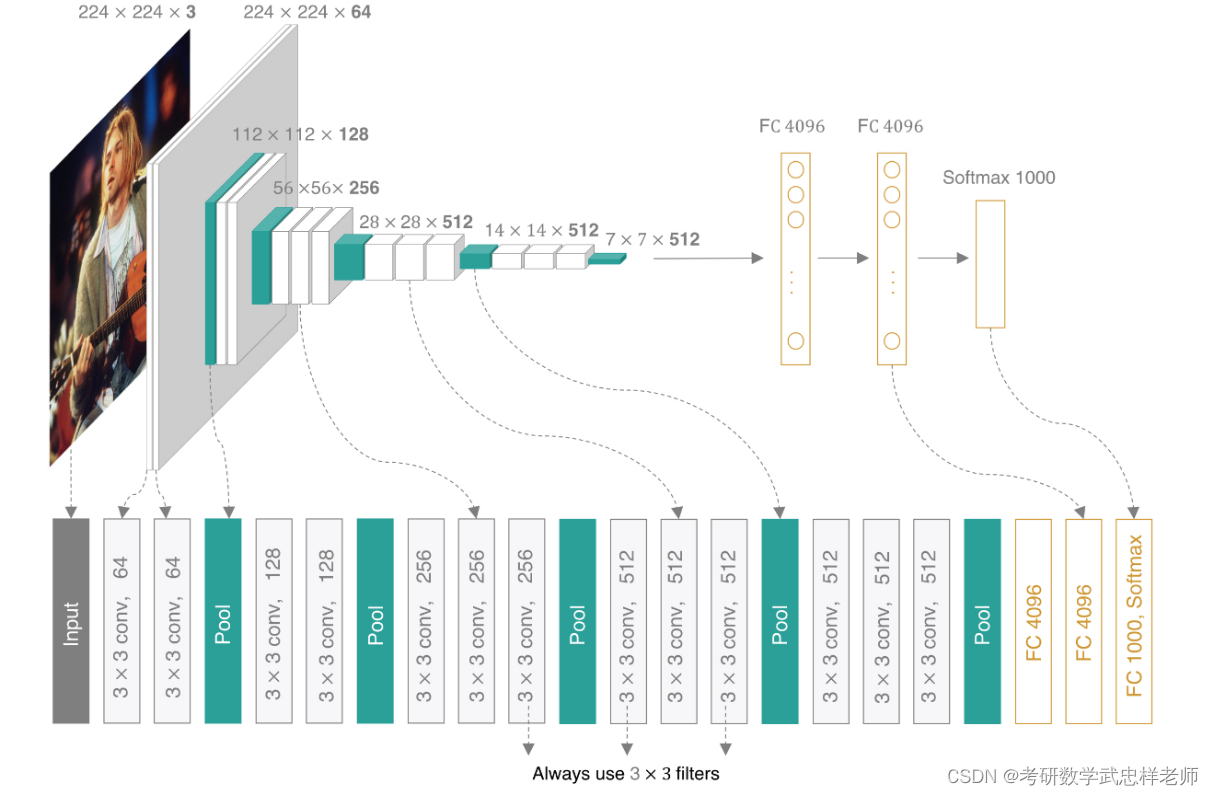
图5.1.2.1. VGG-16网络架构图
5.2. 网络优化与正则化方法
5.2.1. 数据增强
5.2.1.1. 传统方法
深度神经网络一般都需要大量的训练数据才能获得比较理想的效果。在数
据量有限的情况下，可以通过数据增强（Data Augmentation）来增加数据量，提高模型鲁棒性，避免过拟合。目前，数据增强还主要应用在图像数据上，在文本等其他类型的数据上还没有太好的方法。
图像数据的增强主要是通过算法对图像进行转变，引入噪声等方法来增加
数据的多样性。增强的方法主要有几种：
（1）旋转（Rotation）：将图像按顺时针或逆时针方向随机旋转一定角度。
（2）翻转（Flip）：将图像沿水平或垂直方向随机翻转一定角度。
（3）缩放（Zoom In/Out）：将图像放大或缩小一定比例。
（4）平移（Shift）：将图像沿水平或垂直方法平移一定步长。
（5）加噪声（Noise）：加入随机噪声。
我们对数据集进行RandomHorizontalFlip（随机水平翻转）、RandomResizedCrop（随机裁剪）、RandomRotation（随机旋转）、ColorJitter（随机颜色抖动）、RandomAffine（随机仿射变换）、RandomErasing（随机图像擦除）等常规数据增强手段。
5.2.1.2. Mixup数据增强
Mixup是2018年发表在ICLR上的一种数据增强方法，核心思想是从每个batch中随机选择两张图像，并以一定比例混合生成新的图像。需要注意的是，全部训练过程都只采用混合的新图像训练，原始图像不参与训练过程。Mixup的关键思想是通过混合样本和标签，引入数据的多样性和丰富性。这样做的好处是，训练模型可以学习到更广泛的特征表示，提高模型对于不同样本的泛化能力。此外，Mixup还有正则化的效果，可以减少模型的过拟合。
5.2.2. 标签平滑
在数据增强中，我们可以给样本特征加入随机噪声来避免过拟合。同样，我们也可以给样本的标签引入一定的噪声。假设训练数据集中有一些样本的标签是被错误标注的，那么最小化这些样本上的损失函数会导致过拟合。
一种改善的正则化方法是标签平滑（Label Smoothing），即在输出标签中添加噪声来避免模型过拟合。一个样本𝒙的标签可以用one-hot 向量表示。这种标签可以看作硬目标（Hard Target）。如果使用Softmax 分类器并使用交叉熵损失函数，最小化损失函数会使得正确类和其他类的权重差异变得很大。根据Softmax 函数的性质可知，如果要使得某一类的输出概率接近于1，其未归一化的得分需要远大于其他类的得分，可能会导致其权重越来越大，并导致过拟合。此外，如果样本标签是错误的，会导致更严重的过拟合现象。为了改善这种情况，我们可以引入一个噪声对标签进行平滑，即假设样本以𝜖的概率为其他类。其中𝐾为标签数量，这种标签可以看作软目标（Soft Target）。标签平滑可以避免模型的输出过拟合到硬目标上，并且通常不会损害其分类能力。
5.2.3. 学习率策略
学习率是最影响性能的超参数之一，过大的学习率容易造成loss NaN，太小的学习率会导致训练过程非常缓慢。所以在实际训练中，我们都会采用学习率调整的方法。调节的策略有很多，但都大致都遵从一个原则，即学习率在开始训练时很大，在训练过程中逐渐变小，在结束时达到一个最小值。 在本次实验中，主要使用了余弦退火学习率调度器CosineAnnealingLR。如果我们使得网络训练的 loss 最小，那么一直使用较高学习率是不合适的，因为它会使得权重的梯度一直来回震荡，这样就很难使得训练的损失值达到全局最低谷。所以学习率还是需要下降，可以通过余弦函数来降低学习率。余弦函数中随着x的增加余弦值首先缓慢下降，然后加速下降，再次缓慢下降。这种下降模式能和学习率配合，以一种十分有效的计算方式来产生很好的效果。上述过程就称为余弦退火。
5.3. 实验结果与分析
在使用了如上所述的网络优化与正则化方法后，各模型（ResNet-18/20/34、VGG-19、DeseNet-121）的准确率如下：
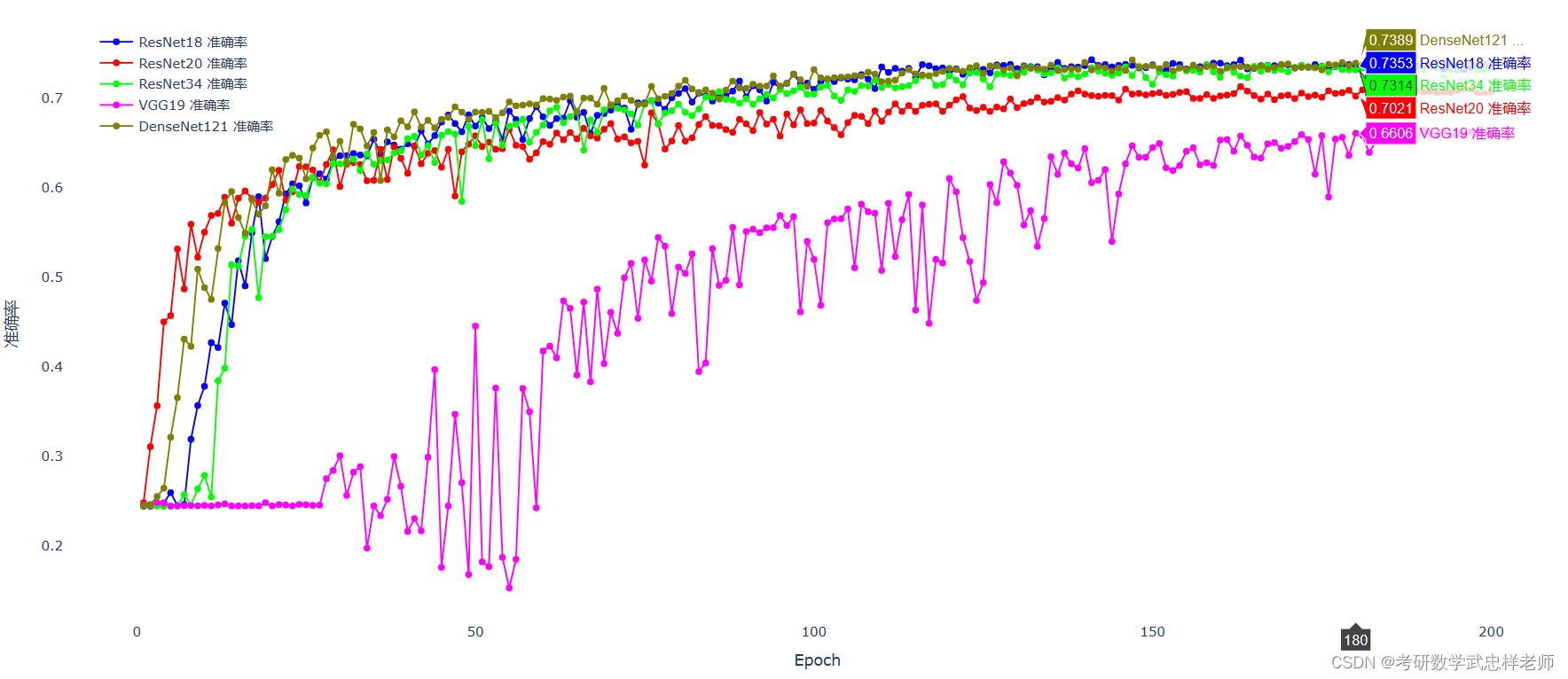
图5.3.1. 各模型准确率对比
我们可以看出，性能上 DenseNet ≥ Resnet＞VGG，这与预期相符。ResNet 比 VGG性能更好的主要原因是它引入了残差连接和残差学习的概念。VGG网络通过增加网络的深度来提高性能，但这会增加梯度消失的风险；而ResNet通过残差连接将前一层的输入直接添加到后续层的输出中，使得梯度能够更容易地传播。这种跳跃连接使得网络中的梯度可以更直接地反向传播，有助于缓解梯度消失问题，使得更深层的网络能够更容易地训练。残差连接使得网络能够学习到残差函数，即网络的学习目标变为学习输入和输出之间的残差。这样的学习方式可以使网络更加关注于学习难以捕捉的细微特征和高频信息，从而提高特征表达能力。由于残差连接的引入，ResNet相对于VGG具有更少的参数数量。在ResNet中，只有残差块中的卷积层需要进行学习，而其他层只是简单的恒等映射。这种设计减少了网络的参数量，使得网络更加轻量化，有助于减少过拟合问题。
DenseNet的性能比ResNet更好的原因主要在于DenseNet中的每个层与之前所有层进行直接连接，形成了密集连接结构，这意味着每个层的输入是由前面所有层的特征图（而不仅仅是前一层的特征图）组合而成的。这种密集连接的设计使得信息在网络中更容易传播和重用，有助于缓解梯度消失问题，并且可以促进特征的多层级复用，从而提高网络的表达能力和性能。与ResNet相比，DenseNet在信息流动和特征重用方面更加强大，因此DenseNet可以被视为ResNet的改进，本次实验也印证了这一点。
分析与总结
本次实验的基本要求部分，我构建了ResNet分类模型18层，在FER2013数据集上达到了65%左右的分类精度；改进方面，我增加了ResNet-20/34/50进行分类并分析了结果及原因；优化方面，我是用了DenseNet-121和VGG-19与ResNet进行对比实验，并加入多种网络优化与正则化方法，最终DenseNet-121达到了最高的分类精度（接近74%），这也验证了DenseNet可以视为ResNet的改进版本。所有实验均在MindSpore与pytorch双平台完成。
本次实验的限制条件主要为本机GPU算力，若没有当前实验环境的限制，则可以使用更深层的模型（如ResNet-152等）进行对比实验，观察残差网络在网络层数不断增加的情况下的性能变化。
附录（主要代码）
标签平滑（Label Smoothing）：
def smooth_one_hot(true_labels: torch.Tensor, classes: int, smoothing=0.0):
# 如果smoothing参数为0，则使用one-hot方法生成标签；如果smoothing参数在0到1之间，则使用平滑方法生成标签
device = true_labels.device
# 获取true_labels张量的设备信息
true_labels = torch.nn.functional.one_hot(
true_labels, classes).detach().cpu()
# detach()从计算图中分离出独热编码的结果，使其成为一个普通的Tensor，与计算图无关
# cpu()方法将结果从GPU转移到CPU上，以便后续处理
assert 0 <= smoothing < 1 # 检查smoothing值是否在0和1之间
confidence = 1.0 - smoothing # 置信度，即正确答案对应的类别概率值
label_shape = torch.Size((true_labels.size(0), classes)) # 二维张量来存储所有标签的概率分布 (总数,类别数)
# 使用torch.no_grad()上下文管理器，禁用梯度计算，因为这段代码不需要反向传播
with torch.no_grad():
true_dist = torch.empty(
size=label_shape, device=true_labels.device) # 存储标签平滑后的标签分布概率值
true_dist.fill_(smoothing / (classes - 1))
_, index = torch.max(true_labels, 1)
true_dist.scatter_(1, torch.LongTensor(
index.unsqueeze(1)), confidence)
'''
将 index 转换成一个二维张量，并且将每个元素变为一个长度为 1 的一维张量，
最终得到的张量的形状为 (batch_size, 1)。
这么做是因为 scatter_() 方法需要传入一个与目标张量同形状的张量作为下标索引，
而 index 张量的形状为 (batch_size,)，无法直接作为下标索引使用。
因此，对 index 扩展一维之后，再转换为 torch.LongTensor 类型的张量，就可以传入 scatter_() 方法中作为下标索引
假设 index 为 [2, 1, 0]，那么 index.unsqueeze(1) 的结果为：
tensor([[2],
[1],
[0]])
'''
return true_dist.to(device)
Mixup数据增强：
def mixup_data(x, y, alpha=0.2):
# 接受三个参数：输入张量x、标签张量y和一个可选的参数alpha，默认值为0.2。
# x:(输入数据的批大小,输入数据的特征维度)
# y:(输入数据的批大小,分类输出的类别数)
if alpha > 0:
lam = np.random.beta(alpha, alpha)
# 从 Beta 分布中生成随机数 根据alpha参数的值生成一个介于0和1之间的随机数lam
else:
lam = 1
batch_size = x.size()[0]
index = torch.randperm(batch_size).cpu()
# 生成一个随机的索引张量index
'''
例如，如果 batch_size=5，则 torch.randperm(batch_size) 可能生成如下随机排列：
tensor([2, 4, 3, 0, 1])
'''
mixed_x = lam * x + (1 - lam) * x[index, :]
# 用lam和1-lam的加权平均值来混合输入张量x和随机索引张量x[index,:]，
y_a, y_b = y, y[index]
return mixed_x, y_a, y_b, lam
# 返回混合后的输入张量mixed_x、原始标签张量y和随机索引张量的标签张量y[index]，以及lam的值。
学习率策略：
optimizer = torch.optim.SGD(model.parameters(
), lr=args.lr, momentum=args.momentum, weight_decay=args.weight_decay, nesterov=True)
# 定义一个优化器optimizer，使用的是随机梯度下降（SGD）算法，
# 其中学习率为args.lr，动量为args.momentum，权重衰减为args.weightdecay，nesterov为True。
# 根据传入的参数args.scheduler的值来选择使用不同的学习率调度器
if args.scheduler == 'cos':
scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(
optimizer, T_max=args.epochs) # 余弦退火学习率调度器
elif args.scheduler == 'reduce':
'''
ReduceLROnPlateau是一种学习率调度器，它可以用于在模型性能不再提升时自适应降低学习率，以更好地优化模型。
具体来说，ReduceLROnPlateau可以监测一个指标（例如验证集上的损失值）在一定周期内是否出现了连续若干次没有进展的情况。
一旦出现这种情况，学习速率就会下降一定比例，继续训练。这种自适应调整可以避免训练过程中的震荡和过拟合问题。
'''
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau( # 学习率衰减学习率调度器
optimizer, mode='max', factor=0.75, patience=5, verbose=True)
'''
当mode为min时，ReduceLROnPlateau将监测评价指标在验证集上的损失值，当损失值达到一个新的最小值时，学习率会更新并减小。
当mode为max时，ReduceLROnPlateau将监测评价指标在验证集上的精度、准确率等指标，当指标达到一个新的最大值时，学习率会更新并减小。
这种方式适用于模型优化的任务需要最大化评价指标的场景，例如人脸识别中的平均精度均值（Mean Average Precision，MAP）评价指标，
当MAP值达到新的最大值时，模型的性能也达到了新的高峰。
'''
# mode参数表示监测量的模式，factor参数表示每次学习率衰减的倍数，patience参数表示当监测量不再改善时，
# 等待几个epoch后再进行学习率调整，verbose参数表示是否输出学习率调整信息。
ResNet：
import torch
import torch.nn as nn
import torch.nn.functional as F
class BasicBlock(nn.Module):
expansion = 1
def __init__(self, in_planes, planes, stride=1):
super(BasicBlock, self).__init__()
self.conv1 = nn.Conv2d(
in_planes, planes, kernel_size=3, stride=stride, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(planes)
self.conv2 = nn.Conv2d(planes, planes, kernel_size=3,
stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(planes)
self.shortcut = nn.Sequential()
'''
如果步长 stride 不为 1 或者输入通道数 in_planes 不等于扩展系数 self.expansion 乘以输出通道数 planes，
则需要进行维度匹配，使用一个包含一个卷积层和一个批量归一化层的序列 self.shortcut 来进行匹配
'''
if stride != 1 or in_planes != self.expansion * planes:
self.shortcut = nn.Sequential(
nn.Conv2d(in_planes, self.expansion * planes,
kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(self.expansion * planes)
)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.bn2(self.conv2(out))
out += self.shortcut(x)
out = F.relu(out)
return out
class Bottleneck(nn.Module):
expansion = 4
def __init__(self, in_planes, planes, stride=1):
super(Bottleneck, self).__init__()
self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=1, bias=False)
self.bn1 = nn.BatchNorm2d(planes)
self.conv2 = nn.Conv2d(planes, planes, kernel_size=3,
stride=stride, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(planes)
self.conv3 = nn.Conv2d(planes, self.expansion *
planes, kernel_size=1, bias=False)
self.bn3 = nn.BatchNorm2d(self.expansion * planes)
self.shortcut = nn.Sequential()
if stride != 1 or in_planes != self.expansion * planes:
self.shortcut = nn.Sequential(
nn.Conv2d(in_planes, self.expansion * planes,
kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(self.expansion * planes)
)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = F.relu(self.bn2(self.conv2(out)))
out = self.bn3(self.conv3(out))
out += self.shortcut(x)
out = F.relu(out)
return out
class ResNet(nn.Module):
def __init__(self, block, num_blocks, num_classes=7):
super(ResNet, self).__init__()
self.in_planes = 64
self.conv1 = nn.Conv2d(1, 64, kernel_size=3, stride=1, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(64)
self.layer1 = self._make_layer(block, 64, num_blocks[0], stride=1)
self.layer2 = self._make_layer(block, 128, num_blocks[1], stride=2)
self.layer3 = self._make_layer(block, 256, num_blocks[2], stride=2)
self.layer4 = self._make_layer(block, 512, num_blocks[3], stride=2)
self.linear = nn.Linear(512 * block.expansion, num_classes)
def _make_layer(self, block, planes, num_blocks, stride):
strides = [stride] + [1] * (num_blocks - 1)
layers = []
for stride in strides:
layers.append(block(self.in_planes, planes, stride))
self.in_planes = planes * block.expansion
return nn.Sequential(*layers)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.layer1(out)
out = self.layer2(out)
out = self.layer3(out)
out = self.layer4(out)
out = F.avg_pool2d(out, 4)
out = out.view(out.size(0), -1)
out = self.linear(out)
return out
def ResNet18():
return ResNet(BasicBlock, [2, 2, 2, 2])
def ResNet34():
return ResNet(BasicBlock, [3, 4, 6, 3])
def ResNet50():
return ResNet(Bottleneck, [3, 4, 6, 3])
def ResNet101():
return ResNet(Bottleneck, [3, 4, 23, 3])
def ResNet152():
return ResNet(Bottleneck, [3, 8, 36, 3])
def test():
net = ResNet50()
y = net(torch.randn(1, 3, 32, 32))
print(y.size())
DenseNet：
import math
import torch
import torch.nn as nn
import torch.nn.functional as F
class Bottleneck(nn.Module):
def __init__(self, in_planes, growth_rate):
super(Bottleneck, self).__init__()
self.bn1 = nn.BatchNorm2d(in_planes)
self.conv1 = nn.Conv2d(in_planes, 4 * growth_rate, kernel_size=1, bias=False)
# 1x1卷积层，它将输入通道数为in_planes的特征图转换为具有4倍growth_rate通道数的特征图。
self.bn2 = nn.BatchNorm2d(4 * growth_rate)
self.conv2 = nn.Conv2d(4 * growth_rate, growth_rate, kernel_size=3, padding=1, bias=False)
# 3x3卷积层，它将具有4倍growth_rate通道数的特征图转换为具有growth_rate通道数的特征图
def forward(self, x):
out = self.conv1(F.relu(self.bn1(x)))
out = self.conv2(F.relu(self.bn2(out)))
out = torch.cat([out, x], 1) # 将新的特征图和输入x在通道维度上进行拼接
return out
# Transition模块的定义，它在DenseNet中用于减小特征图的大小
class Transition(nn.Module):
def __init__(self, in_planes, out_planes):
super(Transition, self).__init__()
self.bn = nn.BatchNorm2d(in_planes)
self.conv = nn.Conv2d(in_planes, out_planes, kernel_size=1, bias=False)
def forward(self, x):
out = self.conv(F.relu(self.bn(x)))
out = F.avg_pool2d(out, 2) # 平均池化操作，将特征图的大小缩小一半
return out
class DenseNet(nn.Module):
def __init__(self, block, nblocks, growth_rate=12, reduction=0.5, num_classes=7):
super(DenseNet, self).__init__()
self.growth_rate = growth_rate
num_planes = 2 * growth_rate
self.conv1 = nn.Conv2d(1, num_planes, kernel_size=3, padding=1, bias=False)
# self.conv1 = nn.Conv2d(3, num_planes, kernel_size=3, padding=1, bias=False)
self.dense1 = self._make_dense_layers(block, num_planes, nblocks[0])
num_planes += nblocks[0] * growth_rate
# 每个 Dense Block 的输入通道数是由上一层的输出通道数加上每个 Bottleneck 层的增长率（growth_rate）
# 乘以该 Dense Block 中的块数（nblocks[0]）得到的
out_planes = int(math.floor(num_planes * reduction))
self.trans1 = Transition(num_planes, out_planes)
num_planes = out_planes
self.dense2 = self._make_dense_layers(block, num_planes, nblocks[1])
num_planes += nblocks[1] * growth_rate
out_planes = int(math.floor(num_planes * reduction))
self.trans2 = Transition(num_planes, out_planes)
num_planes = out_planes
self.dense3 = self._make_dense_layers(block, num_planes, nblocks[2])
num_planes += nblocks[2] * growth_rate
out_planes = int(math.floor(num_planes * reduction))
self.trans3 = Transition(num_planes, out_planes)
num_planes = out_planes
self.dense4 = self._make_dense_layers(block, num_planes, nblocks[3])
num_planes += nblocks[3] * growth_rate
self.bn = nn.BatchNorm2d(num_planes)
self.linear = nn.Linear(num_planes, num_classes)
def _make_dense_layers(self, block, in_planes, nblock):
layers = []
for i in range(nblock):
layers.append(block(in_planes, self.growth_rate))
in_planes += self.growth_rate
return nn.Sequential(*layers)
def forward(self, x):
out = self.conv1(x)
out = self.trans1(self.dense1(out))
out = self.trans2(self.dense2(out))
out = self.trans3(self.dense3(out))
out = self.dense4(out)
out = F.avg_pool2d(F.relu(self.bn(out)), 4)
out = out.view(out.size(0), -1)
# 将特征图展平为一个二维张量，其中第一维度保持批量大小不变，第二维度自动推断为剩余维度的乘积
out = self.linear(out)
return out
def DenseNet121():
return DenseNet(Bottleneck, [6, 12, 24, 16], growth_rate=32)
def DenseNet169():
return DenseNet(Bottleneck, [6, 12, 32, 32], growth_rate=32)
def DenseNet201():
return DenseNet(Bottleneck, [6, 12, 48, 32], growth_rate=32)
def DenseNet161():
return DenseNet(Bottleneck, [6, 12, 36, 24], growth_rate=48)
def densenet_cifar():
return DenseNet(Bottleneck, [6, 12, 24, 16], growth_rate=12)
VGG：
import torch
import torch.nn as nn
cfg = {
'VGG11': [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'VGG13': [64, 64, 'M', 128, 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
'VGG16': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'M', 512, 512, 512, 'M', 512, 512, 512, 'M'],
'VGG19': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 256, 'M', 512, 512, 512, 512, 'M', 512, 512, 512, 512, 'M'],
}
# 每个元素代表一个卷积层的输出通道数，如果元素为 'M'，则表示接下来是一个最大池化层
class VGG(nn.Module):
def __init__(self, vgg_name):
super(VGG, self).__init__()
self.features = self._make_layers(cfg[vgg_name])
self.classifier = nn.Linear(512, 7)
def forward(self, x):
out = self.features(x)
out = out.view(out.size(0), -1)
out = self.classifier(out)
return out
def _make_layers(self, cfg):
layers = []
# in_channels = 3
in_channels = 1
for x in cfg:
if x == 'M':
layers += [nn.MaxPool2d(kernel_size=2, stride=2)]
else:
layers += [nn.Conv2d(in_channels, x, kernel_size=3, padding=1),
nn.BatchNorm2d(x),
nn.ReLU(inplace=True)]
in_channels = x
layers += [nn.AvgPool2d(kernel_size=1, stride=1)]
return nn.Sequential(*layers)
def test():
net = VGG('VGG11')
x = torch.randn(2, 3, 32, 32)
y = net(x)
print(y.size())
# test()
参考文献
[1] 邱锡鹏.神经网络与深度学习[M].北京：机械工业出版社，2020.
[2] 阿斯顿·张等.动手学深度学习[M].北京：人民邮电出版社，2019.
[3] He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.
[4] [EB/OL]. 数据增强mixup技术_Sophia$的博客-CSDN博客
[5] [EB/OL]. 对Pytorch中ResNet源码的探讨_深度科研的博客-CSDN博客
[6] [EB/OL]. 【MindSpore】简单使用Resnet50实现狗狼图片分类。附全部代码下载。_resnet代码下载_闪电丶教主的博客-CSDN博客
[7] [EB/OL]. 图像分类篇：pytorch实现VGG_pytorch vgg_cc巴巴布莱特的博客-CSDN博客
[8] [EB/OL]. Pytorch 实现DenseNet网络_densenet pytorch_乐亦亦乐的博客-CSDN博客
[9] [EB/OL]. https://www.cnblogs.com/jie-74/p/15686416.html
[10] [EB/OL]. MindSpore教程 — MindSpore master documentation
[11] [EB/OL]. 基于pytorch并且使用resnet18 的fer2013人脸识别_fer2013在torchvision中如何调用_宇笨蛋的博客-CSDN博客
[12] [EB/OL]. pytorch余弦退火学习率CosineAnnealingLR的使用_冬日and暖阳的博客-CSDN博客
