二分查找算法

二分查找要点：有序，但是一定全局有序吗？==> 不一定需要全局有序

全局有序概念

一个有序的数组，通过找到 L 和 R 的中点值 ，与目标值比较，来排除一半错误的信息

时间负责度计算

32 16 8 4 2 1 时间负责度 为 log ₂ N

对于每一次 减半的操作 为 O（1）

所以最终时间负责度为 O( log ₂ N)

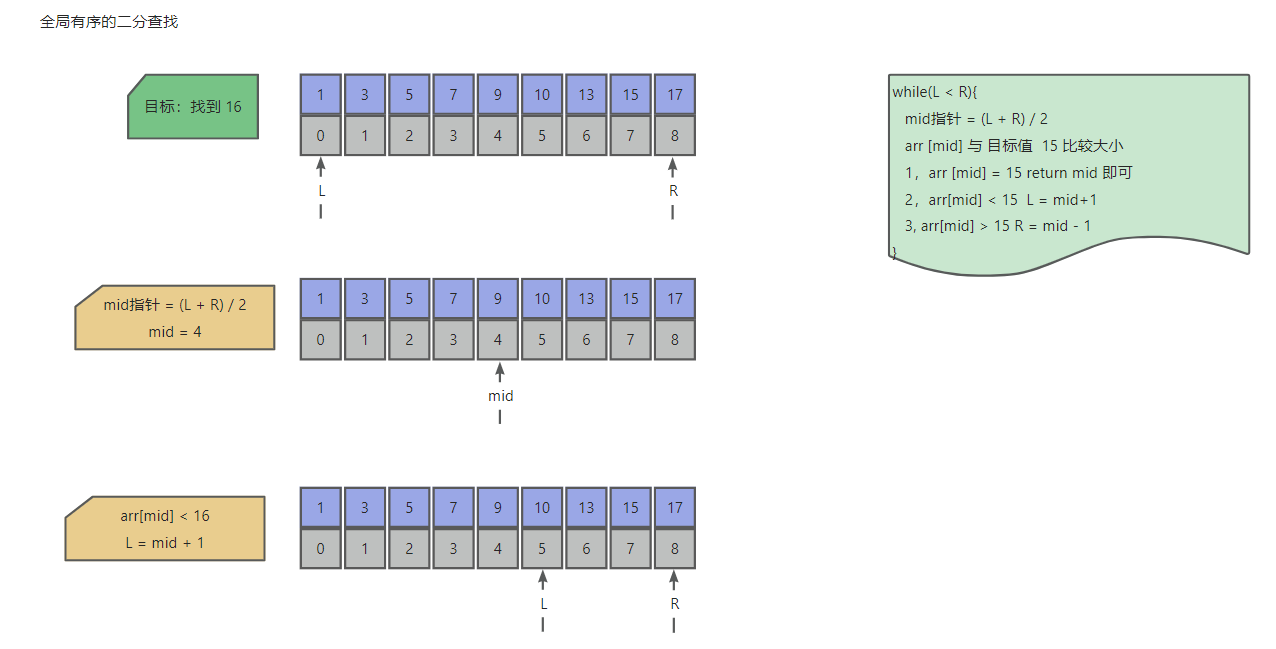
局部有序概念

需要特殊的数据情况，如果能够构建一种排他性的东西 ，左右两侧只要有一半一定有你需要的，如果找到了，直接砍一半就可以了，所以数据特殊的情况，同时满足这类排他性情况，也可以二分

找出某个数

public static Integer getNumForHalf(int[] arr, int num) {
    int N = arr.length - 1;
    int L = 0;
    int R = arr.length - 1;
    while (L <= R) {
        int mid = L + ((R - L) >> 1);
        if ( arr[mid] == num){
            return mid;
        } else if(arr[mid] < num){
            L = mid + 1;
        }else {
            R = mid - 1;
        }
    }
    return null;
}

有序数组查找的数在最左的位置

在已经找到某个数的基础上 依次向左寻找，并记录index，直到值不是目标数为止，找出最右位置同理

public static Integer getNumForHalfLeft(int[] arr, int num) {
    int N = arr.length - 1;
    int L = 0;
    int R = arr.length - 1;
    int indexLeft = -1;
    while (L <= R) {
        int mid = L + ((R - L) >> 1);
        if ( arr[mid] == num){
            indexLeft = mid;
            mid --;
            while (arr[mid] == num){
                indexLeft = mid;
                mid--;
            }
            break;
        } else if(arr[mid] < num){
            L = mid + 1;
        }else {
            R = mid - 1;
        }
    }
    return indexLeft != -1 ? indexLeft : null;
}

局部最小值问题

在一个无序数组中, 值有可能正, 负, 或者零, 数组中任由两个相邻的数一定不相等.
定义局部最小:
1.长度为1，arr[0]就是局部最小；
2.数组的开头，如果arr[0] < arr[1] ，arr[0]被定义为局部最小。
3.数组的结尾，如果arr[N-1] < arr[N-2] ，arr[N-1]被定义为局部最小。
任何一个中间位置i, 即数组下标1~N-2之间, 必须满足arr[i-1] > arr[i] <arr[i+1] ,叫找到一个局部最小。
请找到任意一个局部最小并返回。

思路

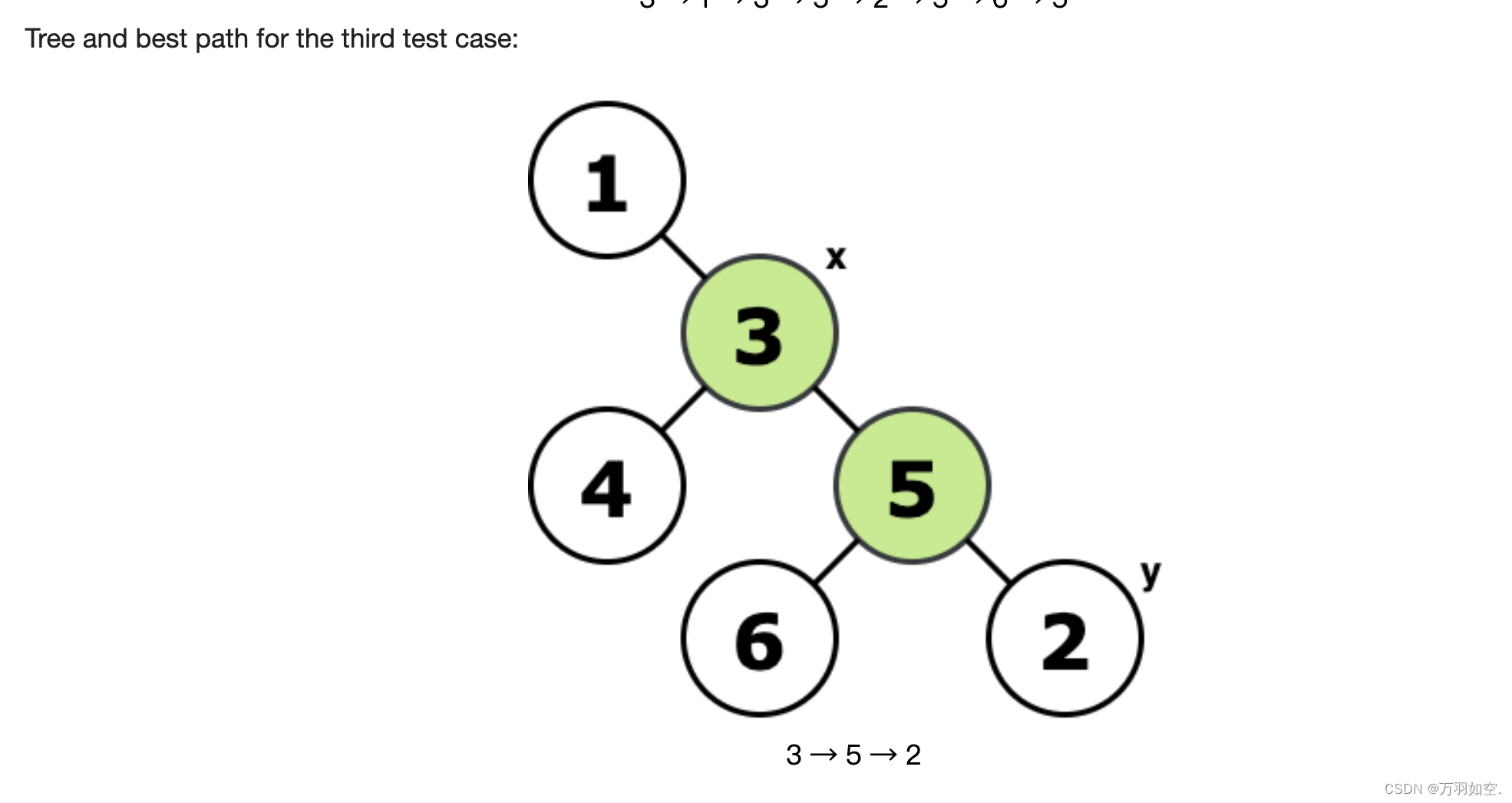
以下图为例

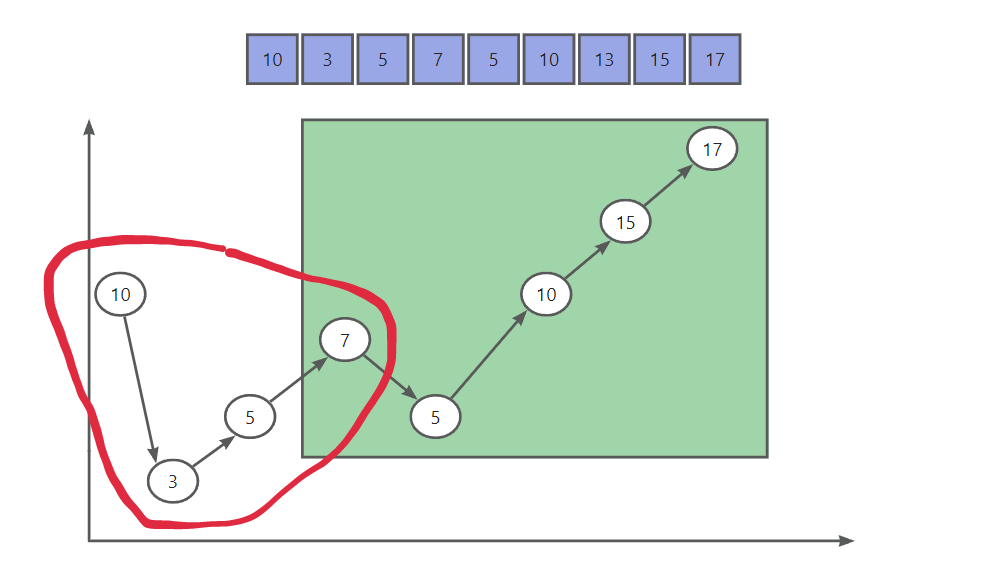
1，如果 同时不满足 arr[0] < arr[1] 和 arr[N-1] < arr[N-2] 那么两边形成的曲线如图

2，此时如果有局部最小，必须满足 在 数组下标1~N-2之间, arr[i-1] < arr[i] <arr[i+1] （即 5 7 5 或 10 3 5 的曲线 ），通过曲线可以看出 先下降后上升，所以形成这样的曲线一定会有一个转折点 比左边小，也比右边小，例如数字 3 ，否则不能形成这样的曲线

3，此时就可以判断

3.1 ， 如果arr[mid-1] > arr[mid] < arr[mid+ 1] 直接返回即可 (如果不满足，最少有一侧式大于mid的)

3.2， 如果arr[mid- 1 ] < arr[mid] 那么 说明 从 mid - 1到 mid的曲线是上升的 ，L 到 mid 重新可以构成先下降后上升的曲线 如图红线框选区域， 所以从L 到 mid 上一定存在局部最小。

3.3，如果arr[mid] > arr[mid + 1] 那么 说明 从 mid 到 mid + 1的曲线是下降的 ，mid 到 R 重新可以构成先下降后上升的曲线 如图绿色框选区域， 所以从mid 到 R 上一定存在局部最小。

public static Integer getNumForHalf(int[] arr) {
    if (arr == null || arr.length == 0){
        return null;
    }

    // 只有 1 个数字  或者 0 < 1
    if(arr.length == 1 || arr[0] < arr[1]){
        return 0;
    }
    if(arr[arr.length - 1 ] < arr[arr.length - 2]){
        return arr.length - 1;
    }

    // 因为 mid 要判断 mid + 1和 -1 所以从 1 和 arr.length - 2 开始
    int L = 1;
    int R = arr.length - 2;
    while (L <= R) {
        int mid = L + ((R - L) >> 1);
        if (arr[mid - 1] > arr[mid] && arr[mid] < arr[mid + 1]){
            return mid;
        } else if (arr[mid - 1] < arr[mid]){
            R = mid + 1;
        } else if (arr[mid] > arr[mid + 1]){
            L = mid - 1;
        }
    }
    return null;
}

都看到着了，点个赞呗