这部分不够熟悉的话,面试直接递归就行。不过实际中虽然递归在某些情况下可以提供简洁和优雅的解决方案,但可能占用大量的内存空间和导致额外时间开销,所以还是尽量使用非递归。因为每次递归调用时,函数的局部变量和参数都需要在栈上创建新的实例,这可能导致栈溢出或耗尽系统资源,尤其是当递归深度很大时。而且递归调用的开销包括函数调用、堆栈帧的创建和销毁等,大规模问题上使用递归可能导致时间性能下降。
目录
- 二叉树中序遍历
对于其他的遍历,只需要画个树写写递归伪代码,和
二叉树中序遍历
给定一个二叉树的根节点root,返回它的中序遍历(“左根右”)结果。
数据范围: 树上节点数满足
0
≤
n
≤
1000
0 \leq n \leq 1000
0≤n≤1000 ,树上每个节点的值满足
−
1000
≤
v
a
l
≤
1000
-1000 \leq v a l \leq 1000
−1000≤val≤1000
要求:空间复杂度
O
(
n
)
O(n)
O(n) ,时间复杂度
O
(
n
)
O(n)
O(n)
树节点:struct类型数据有聚合初始化(Aggregate initialization)、默认成员初始化和成员初始化列表(Member initialization list)等初始化方法,这里自定义构造函数以便使用成员初始化列表初始化
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} //自定义构造函数以便使用成员初始化列表初始化
};
}
创建树和销毁树:
//递归法构建二叉树
int n;
TreeNode* creatTree(vector<int> nums, int index) {
// 二叉树结点x(x指该节点在C++数组中的索引位置)的左孩子在C++数组中的位置等于 2x+1 ,右孩子等于 2x+2 。
if (nums[index] == '#')
return nullptr;
//创建新结点
TreeNode* root= new TreeNode(nums[index]);
printf("The value is %d \n", nums[index]);
//设置左右指针
if (index * 2+1 <= n)
root->left = creatTree(nums, index * 2+1); //找到左孩子
else
root->left = nullptr;
if (index * 2 + 2 <= n)
root->right = creatTree(nums, index * 2 + 2); //找到右孩子
else
root->right = nullptr;
return root;
}
// 注意创建树后不用了需要销毁,这里得手动释放空间
void destroyTree(TreeNode* node) {
if (node == nullptr) {
return;
}
destroyTree(node->left);
destroyTree(node->right);
printf("destroy node value is %d \n", node->val);
delete node;
}
两种实现中序遍历的方法:利用栈非递归,递归
vector<int> inorderTraversal(TreeNode* root) { //非递归方法
vector<int> res; // 存放中序遍历的输出值
stack<TreeNode*> st; // 栈中存放结点
TreeNode* p = root;
while (!st.empty() || p) // p等于空说明根节点为空或者到了叶子节点的某个空子节点
{// 循环条件为 【st非空 或者 p指向确定对象时(使用指针变量进行条件判断时,当指针变量为nullptr时,条件判断为假)】
// 终止条件为 【st为空,且p等于nullptr】
while (p) //一直沿左子树向下
{
st.push(p); // 由于st是栈,父节点先进入,后出
p = p->left;
}
TreeNode* tt = st.top(); //到达叶子节点的某个空子节点,返回
st.pop();
res.push_back(tt->val);
p = tt->right; // 去检查右节点
}
return res;
}
void inorder(vector<int>& res, TreeNode* root) {
//遇到空节点则返回
if (root == NULL)
return;
//先遍历左子树
inorder(res, root->left);
//再遍历根节点
res.push_back(root->val);
//最后遍历右子树
inorder(res, root->right);
}
vector<int> inorderTraversal2(TreeNode* root) {
vector<int> res;
//递归中序遍历
inorder(res, root);
return res;
}
main函数测试:
int main() {
// 创建一颗树{1,2,#,#,3}
vector<int> nums = { 1,2,'#','#',3 };
n = nums.size();
TreeNode* root = creatTree(nums, 0);
vector<int> Non_recursice_res = inorderTraversal(root);
cout << "非递归中序遍历:" << ' ';
for (auto& element : Non_recursice_res) {
std::cout << element << " ";
}
std::cout << std::endl;
vector<int> recursice_res = inorderTraversal(root);
cout<< "递归中序遍历:" << ' ';
for (auto& element : recursice_res) {
std::cout << element << " ";
}
std::cout << std::endl;
destroyTree(root);
}
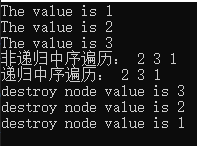
测试结果: