for Many-objective Optimization)

目标函数

$$\underset{X}{\min }f(X)=(f_1(X),f_2(X),...,f_M(X))$$

预备知识

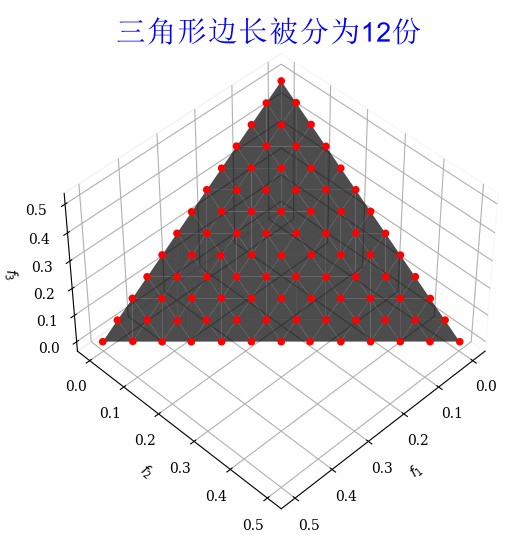
参考向量个数 $N=C_{H+M-1}^{M-1}$， $H$ 为边长分成的份数， $M$是目标的个数

from pymoo.algorithms.moo.rvea import RVEA
from pymoo.optimize import minimize
from pymoo.problems import get_problem
from pymoo.util.ref_dirs import get_reference_directions
from pymoo.visualization.scatter import Scatter

problem = get_problem("dtlz1", n_obj=3)

ref_dirs = get_reference_directions("das-dennis", 3, n_partitions=12)

algorithm = RVEA(ref_dirs)

res = minimize(problem,
               algorithm,
               termination=('n_gen', 400),
               seed=1,
               verbose=False)

plot = Scatter()
plot.add(problem.pareto_front(ref_dirs), plot_type="surface", color="black", alpha=0.7)
plot.add(res.F, color="red")
plot.show(block=True)

此代码中$H=n\_partitions=12M=n\_obj=3$

故最终的参考向量个数$N=C_{12+3-1}^{3-1}=C_{14}^2=91$

每个参考向量需要单位化：$v_i=\frac{u_i}{||u_i||}$

参考向量的相似度$cos\theta =\frac{v_1\bullet v_2}{||v_1||||v_2||}$

参考向量引导选择

• 理想向量：$Z_t^{min}=(Z_{t,1}^{min},Z_{t,2}^{min},...,Z_{t,m}^{min})$代表每个目标函数的最小值组成的向量

• 目标向量平移：因为参考向量是以坐标系原点为中心的，因此需要将目标函数都平移到坐标系原点：${\text{f}}_{t,i}^{\prime }={\text{f}}_{t,i}-Z_t^{min}$，${\text{f}}_{t,i}$表示第$t$次迭代中第$i$个个体的目标函数向量

• 种群划分：种群里面的每个个体按照到参考向量的最小夹角，与离得最近的目标向量归为一个集合体【与目标向量的余弦值最大】
  c o s θ t , i , j = f t , i ′ ∙ v t , j ∣ ∣ f t , i ′ ∣ ∣ P ˉ t , k = { I t , i ∣ k = argmax i ∈ { 1 , 2 , . . . , N } c o s θ t , i , j } \begin{align} cos \theta_{t, i, j} &= \frac{\text{f}_{t, i}^{\prime} \bullet \pmb{v}_{t, j}}{||\text{f}_{t, i}^{\prime}||} \\ \bar{P}_{t, k} &= \{I_{t, i}|k = \underset{i \in \{1, 2, ..., N\}}{\text{argmax}} cos \theta_{t, i, j}\} \end{align} cosθt,i,j​Pˉt,k​​=∣∣ft,i′​∣∣ft,i′​∙vt,j​​={It,i​∣k=i∈{1,2,...,N}argmax​cosθt,i,j​}​​

• 角度惩罚距离
  d t , i , j = ( 1 + P ( θ t , i , j ) ) ∙ ∣ ∣ f t , i ′ ∣ ∣ P ( θ t , i , j ) = M . ( t t m a x ) α . θ t , i , j γ v t , j γ v t , j = min ⁡ i ∈ { 1 , 2 , . . . , N } , i ≠ j < v t , i , v t , j >          最小角 \begin{align} d_{t, i, j} &= (1 + P(\theta_{t, i, j})) \bullet ||\text f_{t, i}^{\prime}|| \\ P(\theta_{t, i, j}) &= M . (\frac{t}{t_{max}}) ^\alpha . \frac{\theta_{t, i, j}}{\gamma_{\pmb v_{t, j}}} \\ \gamma_{\pmb v_{t, j}} &= \min_{i \in \{1, 2, ..., N\}, i \neq j} <\pmb v_{t, i}, \pmb v_{t, j}> \;\;\;\; \text{最小角} \end{align} dt,i,j​P(θt,i,j​)γvt,j​​​=(1+P(θt,i,j​))∙∣∣ft,i′​∣∣=M.(tmax​t​)α.γvt,j​​θt,i,j​​=i∈{1,2,...,N},i=jmin​<vt,i​,vt,j​>最小角​​

更新参考向量

$$v_{t+1,i}=\frac{v_{0,i}\circ (Z_{t+1}^{max}-Z_{t+1}^{min})}{||v_{0,i}\circ (Z_{t+1}^{max}-Z_{t+1}^{min})||}$$

流程

整体框架

参考向量引导选择

参考向量自适应

fr通常设置为$0.2$